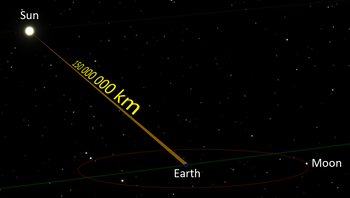
Ánh sáng Mặt Trời mất khoảng 8 phút 17 giây để đi từ Mặt Trời đến Trái Đất (theo khoảng cách trung bình). | |
| Giá trị trung bình | |
|---|---|
| mét trên giây | 299792458 |
| đơn vị Planck | 1 |
| Giá trị xấp xỉ | |
| kilômét trên giờ | 1,08 tỷ |
| dặm trên giây | 186.000 |
| dặm trên giờ | 671 triệu |
| đơn vị thiên văn trên ngày | 173 |
| Xấp xỉ khoảng thời gian ánh sáng đi qua | |
| Khoảng cách | Thời gian |
| một foot | 1,0 ns |
| một mét | 3,3 ns |
| từ quỹ đạo địa tĩnh đến Trái Đất | 119 ms |
| chu vi xích đạo Trái Đất | 134 ms |
| từ Mặt Trăng đến Trái Đất | 1,3 s |
| từ Mặt Trời đến Trái Đất (1 AU) | 8,3 min |
| từ ngôi sao gần nhất đến Mặt Trời (1,3 pc) | 4,2 năm |
| từ thiên hà gần nhất (thiên hà lùn Canis Major) đến Trái Đất | khoảng 25.000 năm |
| băng qua Ngân Hà | khoảng 100.000 năm |
| từ thiên hà Andromeda đến Trái Đất | khoảng 2,5 triệu năm |
| Thuyết tương đối hẹp |
|---|
|
|
Nền tảng[hiện] |
|
Hệ quả[hiện] |
|
Không–thời gian[hiện] |
|
Động lực học[hiện] |
|
|
Nhà nghiên cứu[hiện] |
|
Các công thức khác của thuyết tương đối hẹp |
Vận tốc ánh sáng trong chân không, ký hiệu c, là một hằng số vật lý quan trọng trong nhiều lĩnh vực khoa học. Giá trị chính xác của nó là 299.792.458 m/s, tương đương khoảng 300.000 km/s, là tốc độ nhanh nhất mà chúng ta biết đến và có thể ứng dụng trong các nghiên cứu khoa học. Theo thuyết tương đối hẹp, c là tốc độ tối đa mà mọi dạng năng lượng, vật chất, và thông tin trong vũ trụ có thể đạt được. Đây là tốc độ của các hạt không có khối lượng liên kết với các trường vật lý (bao gồm bức xạ điện từ như photon ánh sáng) trong chân không, cũng như tốc độ truyền của hấp dẫn (như sóng hấp dẫn) theo lý thuyết hiện tại. Các hạt và sóng truyền với tốc độ c không bị ảnh hưởng bởi chuyển động của nguồn hoặc hệ quy chiếu quán tính của người quan sát. Trong thuyết tương đối, c liên kết với không gian và thời gian, và xuất hiện trong phương trình nổi tiếng về sự tương đương khối lượng-năng lượng E = mc.
Khi ánh sáng di chuyển qua các vật liệu trong suốt như thủy tinh hay không khí, vận tốc của nó giảm xuống so với c. Tỉ số giữa c và vận tốc v của ánh sáng trong vật liệu được gọi là chỉ số khúc xạ n của vật liệu (n = c / v). Ví dụ, chỉ số khúc xạ của thủy tinh với ánh sáng nhìn thấy có giá trị khoảng 1,5, có nghĩa là ánh sáng di chuyển qua thủy tinh với vận tốc khoảng c / 1,5 ≈ 200000 km/s; chỉ số khúc xạ của không khí đối với ánh sáng nhìn thấy là 1,0003, vì vậy vận tốc của ánh sáng trong không khí chậm hơn 90 km/s so với c.
Trong thực tế hàng ngày, ánh sáng có thể coi là truyền đi gần như ngay lập tức, nhưng với khoảng cách lớn và các phép đo rất nhạy, sự hạn chế của tốc độ ánh sáng có thể được nhận thấy. Ví dụ, trong các video ghi lại cơn bão với tia sét từ Trạm Vũ trụ Quốc tế ISS, hình ảnh của tia sáng từ chớp có thể được quan sát, cho phép các nhà khoa học ước lượng tốc độ ánh sáng bằng cách phân tích các khung hình của tia sáng. Điều này không gây ngạc nhiên vì thời gian ánh sáng để vòng quanh chu vi Trái Đất là khoảng 140 ms. Hiện tượng này cũng giải thích cho cộng hưởng Schumann. Khi truyền tín hiệu thông tin đến các tàu không gian, thời gian từ vài phút đến vài giờ để tín hiệu đến Trái Đất và ngược lại. Ánh sáng từ các ngôi sao đến với chúng ta mất nhiều năm, cho phép các nhà thiên văn nghiên cứu lịch sử vũ trụ qua việc quan sát các thiên thể xa xôi. Tốc độ ánh sáng hữu hạn cũng đặt ra giới hạn lý thuyết cho tốc độ tính toán của máy tính, vì thông tin dưới dạng bit truyền qua tín hiệu điện giữa các bộ vi xử lý. Cuối cùng, tốc độ ánh sáng có thể được dùng để đo lường khoảng cách lớn với độ chính xác cao.
Vào năm 1676, Ole Rømer là người đầu tiên chứng minh rằng ánh sáng có tốc độ hữu hạn, thay vì tốc độ tức thì như được tin tưởng trước đó, thông qua nghiên cứu chuyển động của vệ tinh Io của Sao Mộc. Đến năm 1865, James Clerk Maxwell dựa trên lý thuyết điện từ của mình đã chứng minh ánh sáng là sóng điện từ, với hằng số c xuất hiện trong các phương trình sóng của ông. Năm 1905, Albert Einstein đưa ra tiên đề rằng tốc độ ánh sáng trong chân không là không đổi đối với mọi hệ quy chiếu quán tính và không phụ thuộc vào chuyển động của nguồn sáng, từ đó xây dựng thuyết tương đối hẹp và chỉ ra rằng c có ý nghĩa sâu xa hơn ngoài tốc độ ánh sáng và sóng điện từ. Sau nhiều thập kỷ đo lường chính xác, năm 1975 tốc độ ánh sáng trong chân không được định nghĩa lại là 299792458 m/s với sai số 4 phần tỷ. Năm 1983, đơn vị mét được định nghĩa lại trong hệ SI bằng khoảng cách ánh sáng truyền trong chân không trong thời gian bằng 1/299.792.458 của một giây, làm cho giá trị c trong đơn vị mét trên giây được xác định cố định và chính xác.
Giá trị, ký hiệu và đơn vị
Tốc độ ánh sáng trong chân không được ký hiệu là c. Ký hiệu c xuất phát từ từ 'constant' (hằng số) trong hệ đo lường vật lý và cũng từ từ Latin 'celeritas', có nghĩa là 'nhanh chóng' hay 'tốc độ'. (Chữ C hoa trong đơn vị SI đại diện cho coulomb, đơn vị đo điện tích.) Ban đầu, ký hiệu V được dùng để chỉ tốc độ ánh sáng, theo James Clerk Maxwell vào năm 1865. Năm 1856, Wilhelm Eduard Weber và Rudolf Kohlrausch đã sử dụng c cho một hằng số khác mà sau này được xác định là √2 lần tốc độ ánh sáng trong chân không. Đến năm 1894, Paul Drude đã xác định lại c theo cách sử dụng hiện đại. Einstein đã dùng V trong bài báo về thuyết tương đối hẹp năm 1905, nhưng từ năm 1907, ông chuyển sang sử dụng c, và từ đó c trở thành ký hiệu chuẩn cho tốc độ ánh sáng.
Thỉnh thoảng, c được dùng để chỉ tốc độ sóng trong các vật liệu khác nhau, và c0 là ký hiệu cho tốc độ ánh sáng trong chân không. Ký hiệu với chỉ số dưới, như được dùng trong các tài liệu chính thức của hệ SI, tương tự như các hằng số liên quan: μ0 cho hằng số từ môi hoặc hằng số từ, ε0 cho hằng số điện môi hoặc hằng số điện, và Z0 cho trở kháng chân không. Trong bài viết này, c được dùng để chỉ tốc độ ánh sáng trong chân không.
Trong hệ SI, mét được định nghĩa là khoảng cách ánh sáng đi qua chân không trong thời gian bằng 1/299792458 của một giây. Định nghĩa này cố định giá trị tốc độ ánh sáng trong chân không chính xác là 299792458 m/s. Là một hằng số vật lý có thứ nguyên, giá trị của c có thể khác nhau tùy thuộc vào hệ đơn vị. Trong các lĩnh vực vật lý có sự xuất hiện của c, như thuyết tương đối, các nhà vật lý thường sử dụng hệ đơn vị tự nhiên hoặc hệ đơn vị hình học với c = 1. Trong các hệ đo này, c không xuất hiện trong các phương trình vật lý vì giá trị của nó bằng 1 không ảnh hưởng đến kết quả của các đại lượng khác.
Vai trò nền tảng trong vật lý
Tốc độ ánh sáng trong chân không không bị ảnh hưởng bởi chuyển động của nguồn sáng cũng như hệ quy chiếu của người quan sát. Tính bất biến của tốc độ ánh sáng, được Einstein đưa ra như một tiên đề trong thuyết tương đối hẹp năm 1905, đã được xác nhận qua nhiều thí nghiệm sau khi lý thuyết điện từ cổ điển của Maxwell không cung cấp bằng chứng cho sự tồn tại của vật chất siêu sáng. Mặc dù không thể đo tốc độ ánh sáng trên một đường truyền đơn (ví dụ, từ một nguồn ở xa), vì không thể bỏ qua quy ước đồng bộ hóa giữa đồng hồ, tốc độ ánh sáng trên hai đường truyền (ví dụ, từ nguồn đến gương phản xạ và trở về) được xác nhận độc lập với hệ quy chiếu. Bằng cách áp dụng phương pháp đồng bộ hóa của Einstein, tốc độ ánh sáng trên đường truyền đơn được coi bằng tốc độ ánh sáng trên hai đường truyền. Thuyết tương đối hẹp tiết lộ những hệ quả kỳ lạ từ tiên đề về bất biến của c và các định luật vật lý giống nhau trong mọi hệ quy chiếu quán tính. Một hệ quả là tốc độ của mọi hạt không khối lượng và sóng, bao gồm ánh sáng, trong chân không đều bằng c.
Thuyết tương đối hẹp mang lại nhiều kết quả phản trực giác, và các kết quả này đã được xác nhận thực nghiệm. Chúng bao gồm nguyên lý tương đương giữa khối lượng và năng lượng (E = mc), sự co ngắn độ dài (các vật chuyển động trông ngắn hơn), và sự giãn nở thời gian (các đồng hồ chuyển động chạy chậm hơn). Hệ số γ, được gọi là hệ số Lorentz, xác định mức độ co ngắn độ dài và giãn nở thời gian, và được tính bằng công thức γ = (1 − v/c), với v là vận tốc của vật. Sự khác biệt giữa γ và 1 có thể bỏ qua khi tốc độ của vật nhỏ hơn nhiều so với c, ví dụ như trong các vận tốc hàng ngày—trong thuyết tương đối hẹp, điều này gần bằng nguyên lý tương đối Galileo—nhưng hệ số này sẽ tăng lên và tiến tới vô hạn khi v tiến gần đến c.
Các kết quả của thuyết tương đối hẹp có thể được tổng hợp bằng cách xem không gian và thời gian là một cấu trúc thống nhất gọi là không-thời gian (với c liên hệ giữa các đơn vị không gian và thời gian), và yêu cầu các lý thuyết vật lý phải thỏa mãn đối xứng đặc biệt gọi là bất biến Lorentz, trong đó các công thức của các lý thuyết này chứa hằng số c. Bất biến Lorentz là giả thuyết phổ quát trong các lý thuyết vật lý hiện đại như điện động lực học lượng tử, sắc động lực học lượng tử, Mô hình chuẩn của vật lý hạt, thuyết tương đối tổng quát và mô hình Vụ Nổ Lớn. Do đó, tham số c rất phổ biến trong vật lý hiện đại và xuất hiện trong nhiều phương trình không liên quan đến ánh sáng. Ví dụ, trong thuyết tương đối rộng, c cũng là tốc độ truyền của trường hấp dẫn hay sóng hấp dẫn. Trong các hệ quy chiếu không-quán tính (không-thời gian cong trong thuyết tương đối tổng quát và trong các hệ quy chiếu có gia tốc), tốc độ ánh sáng cục bộ là hằng số và bằng c, nhưng tốc độ ánh sáng dọc theo một quỹ đạo hữu hạn có thể khác c, tùy thuộc vào cách định nghĩa khoảng cách và thời gian.
Các nhà vật lý thường giả định rằng các hằng số cơ bản như c giữ nguyên giá trị trong nhiều vùng không-thời gian, có nghĩa là chúng không phụ thuộc vào vị trí và không thay đổi theo thời gian. Tuy nhiên, một số lý thuyết gợi ý rằng tốc độ ánh sáng có thể biến đổi theo thời gian. Mặc dù chưa có bằng chứng thực nghiệm được công nhận rộng rãi về sự thay đổi của các hằng số, vấn đề này vẫn là một chủ đề nghiên cứu tiếp tục.
Các nhà vật lý cũng giả định rằng tốc độ ánh sáng là đồng nhất, tức là nó có giá trị như nhau trong mọi hướng đo. Các quan sát bức xạ từ mức năng lượng hạt nhân theo hướng phát xạ riêng trong từ trường (như thí nghiệm Hughes-Drever) và các máy cộng hưởng quang học (như thí nghiệm Michelson-Morley) đã đặt ra các giới hạn chặt chẽ đối với khả năng tốc độ ánh sáng không đồng nhất trong các thí nghiệm hai đường truyền.
Giới hạn tối đa của tốc độ
Theo thuyết tương đối hẹp, năng lượng của một vật có khối lượng nghỉ m và vận tốc v được tính bằng công thức E = γmc, với γ là hệ số Lorentz đã đề cập. Khi v bằng 0, γ bằng 1, và ta có công thức nổi tiếng E = mc cho sự tương đương giữa khối lượng và năng lượng. Hệ số γ tiến tới vô hạn khi v gần bằng c, điều này cho thấy cần một năng lượng vô hạn để gia tốc vật có khối lượng lên tốc độ ánh sáng. Tốc độ ánh sáng là giới hạn trên cho tốc độ của mọi vật có khối lượng nghỉ dương, và điều này đã được xác nhận qua nhiều thí nghiệm về năng lượng và động lượng tương đối tính.
Một nguyên lý cơ bản của thuyết tương đối hẹp là không có thông tin hay năng lượng nào có thể di chuyển nhanh hơn ánh sáng. Ví dụ, khái niệm về sự đồng thời có thể khác nhau giữa các hệ quy chiếu. Nếu khoảng cách giữa hai sự kiện A và B lớn hơn khoảng thời gian giữa chúng nhân với tốc độ ánh sáng c, thì trong một số hệ quy chiếu, A có thể xảy ra trước B, trong khi trong các hệ khác, B có thể xảy ra trước A, hoặc cả hai sự kiện có thể xảy ra đồng thời. Điều này dẫn đến khả năng một vật di chuyển nhanh hơn c có thể quay ngược thời gian trong một hệ quy chiếu khác, vi phạm nguyên lý nhân quả, khiến cho 'hiệu ứng' có thể xuất hiện trước 'nguyên nhân' của nó. Vi phạm nguyên lý này chưa bao giờ được quan sát và có thể dẫn đến các nghịch lý như phản điện thoại tachyon (tachyonic antitelephone).
Khám phá và thí nghiệm về tốc độ nhanh hơn ánh sáng
Có những tình huống dường như cho thấy vật chất, năng lượng, hoặc thông tin di chuyển nhanh hơn tốc độ ánh sáng c, nhưng thực tế không phải như vậy. Ví dụ, như đã đề cập trong phần sự lan truyền của ánh sáng trong môi trường phía dưới, nhiều loại sóng có thể di chuyển nhanh hơn c. Cụ thể, tốc độ pha của tia X đi qua hầu hết các loại thủy tinh có thể vượt c, nhưng sóng này không mang theo thông tin vật lý.
Khi một chùm laser quét nhanh qua một vật ở xa, điểm sáng có thể dường như di chuyển nhanh hơn c, mặc dù sự chuyển động của điểm sáng này bị trì hoãn bởi thời gian ánh sáng cần để đến vật ở xa (vẫn luôn bằng c trong chân không). Tuy nhiên, chỉ có tia laser di chuyển và phát ra ánh sáng với tốc độ c từ laser đến nhiều vị trí của điểm. Tương tự, bóng của hình chiếu trên một vật thể xa có thể trông như di chuyển nhanh hơn ánh sáng, sau một thời gian trễ. Trong tất cả các trường hợp, không có vật chất, năng lượng, hoặc thông tin nào chuyển động nhanh hơn ánh sáng.
Tốc độ thay đổi khoảng cách giữa hai vật trong cùng một hệ quy chiếu mà chúng đang chuyển động có thể vượt quá c. Tuy nhiên, tốc độ này không phản ánh tốc độ của từng vật theo quan sát của một hệ quy chiếu quán tính.
Hiệu ứng lượng tử, chẳng hạn như nghịch lý EPR, dường như cho thấy thông tin có thể truyền nhanh hơn ánh sáng c. Trong thí nghiệm tưởng tượng này, hai hạt có trạng thái lượng tử bị vướng víu với nhau. Trước khi các hạt được quan sát hoặc đo, chúng tồn tại trong một trạng thái chồng chập. Khi một trong hai hạt được đo, trạng thái lượng tử của hạt còn lại được xác định ngay lập tức, dù chúng có thể cách xa nhau. Tuy nhiên, chúng ta không thể biết trước trạng thái lượng tử của hạt đầu tiên, nên thông tin không thực sự được truyền theo cách thông thường.
Một hiệu ứng lượng tử khác có thể gây ấn tượng là hiệu ứng Hartman, dự đoán sự di chuyển nhanh hơn ánh sáng. Theo hiệu ứng này, thời gian cần để một hạt ảo vượt qua hàng rào là hằng số, không phụ thuộc vào độ dày của hàng rào. Điều này dẫn đến việc hạt ảo có thể di chuyển qua khoảng cách lớn với tốc độ nhanh hơn ánh sáng. Tuy nhiên, không có thông tin nào có thể được truyền đi bằng cách sử dụng hiệu ứng này.
Có hiện tượng chuyển động nhanh hơn ánh sáng khi quan sát các thiên thể, như các tia tương đối tính từ các thiên hà vô tuyến hoặc quasar. Tuy nhiên, đây không phải là sự di chuyển với tốc độ vượt ánh sáng; chỉ là hiệu ứng hình chiếu do vật (hạt) di chuyển gần tốc độ ánh sáng và tạo ra góc nhỏ với hướng nhìn: ánh sáng phát ra từ các hạt ở xa sẽ mất nhiều thời gian hơn để đến Trái Đất, làm cho khoảng cách giữa hai lần quan sát có vẻ lớn hơn.
Trong mô hình vũ trụ giãn nở, thiên hà càng xa thì vận tốc lùi ra xa càng lớn. Điều này không phải là do chuyển động của thiên hà trong không gian mà là do sự giãn nở của không gian. Ví dụ, thiên hà xa Trái Đất di chuyển lùi với tốc độ tỷ lệ thuận với khoảng cách của nó. Khi khoảng cách vượt qua mặt cầu Hubble, vận tốc của các thiên hà sẽ vượt quá tốc độ ánh sáng khi khoảng cách đến Trái Đất rất lớn.
Vào tháng 9 năm 2011, các nhà vật lý tại thí nghiệm OPERA công bố rằng chùm hạt neutrino từ CERN (Genève, Thụy Sĩ) đến phòng thí nghiệm Gran Sasso (Italia) di chuyển nhanh hơn tốc độ ánh sáng. Kết quả này, được gọi là 'neutrino chuyển động siêu sáng', sau đó được xác nhận là có sai số do các sợi quang học bị hỏng, làm ảnh hưởng đến độ chính xác của đo lường.
Đặc tính truyền dẫn của ánh sáng
Trong vật lý cổ điển, ánh sáng được xem là một dạng bức xạ điện từ. Các đặc điểm của trường điện từ được mô tả qua phương trình Maxwell, cho biết tốc độ truyền sóng điện từ c (như ánh sáng) trong chân không liên quan đến hằng số điện môi ε0 và hằng số từ môi μ0 qua phương trình c = 1/√ε0μ0. Trong cơ học lượng tử, trường điện từ được mô tả qua lý thuyết điện động lực học lượng tử (QED), theo đó ánh sáng là trạng thái cơ bản (hoặc lượng tử) của trường điện từ, gọi là photon. Photon là hạt không khối lượng và do đó, theo thuyết tương đối hẹp, chúng chuyển động với tốc độ ánh sáng trong chân không.
Một số lý thuyết mở rộng QED, trong đó photon có khối lượng, cũng đã được nghiên cứu. Theo những lý thuyết này, tốc độ của photon phụ thuộc vào tần số của nó, và tốc độ ánh sáng c có thể là giới hạn trên trong thuyết tương đối hẹp. Chưa có hiệu ứng thay đổi tốc độ ánh sáng theo tần số được xác nhận qua các thí nghiệm phức tạp, điều này đặt ra giới hạn chặt chẽ cho khối lượng của photon. Giới hạn này thay đổi theo từng mô hình lý thuyết: nếu photon có khối lượng như trong thuyết Proca, giới hạn thực nghiệm cho khối lượng photon là 10 gram; còn nếu khối lượng photon được mô tả qua cơ chế Higgs, giới hạn khối lượng là m ≤ 10 eV/c (khoảng 2 × 10 g).
Một lý do khác khiến tốc độ ánh sáng có thể thay đổi theo tần số là do thuyết tương đối hẹp có thể không còn áp dụng cho các hệ vật lý vi mô, như một số lý thuyết về hấp dẫn lượng tử dự đoán. Vào năm 2009, khi quan sát phổ từ chớp gamma GRB 090510, các nhà thiên văn không phát hiện sự khác biệt về tốc độ của các photon có năng lượng khác nhau, và xác nhận rằng bất biến Lorentz vẫn chính xác ít nhất đến cấp độ dài Planck (lP = √ħ G/c ≈ 16163×10 m) chia cho 1,2.
Trong môi trường
Trong các môi trường, ánh sáng thường không truyền đi với tốc độ bằng c; hơn nữa, ánh sáng có các bước sóng khác nhau sẽ di chuyển với tốc độ khác nhau. Đối với sóng phẳng (sóng phủ toàn không gian, chỉ có một tần số), tốc độ mà điểm có pha dao động di chuyển theo hướng nhất định được gọi là tốc độ pha vp. Một tín hiệu vật lý thực với độ mở hữu hạn (như xung ánh sáng) có các thành phần di chuyển với tốc độ khác nhau. Phần lớn của xung (biên độ sóng) di chuyển với tốc độ nhóm vg, trong khi phần đầu tiên di chuyển với tốc độ đầu sóng vf.
Tốc độ pha đóng vai trò quan trọng trong việc xác định cách ánh sáng lan truyền qua các vật liệu hoặc từ môi trường này sang môi trường khác. Nó thường được ký hiệu bằng chiết suất. Chiết suất của một vật liệu được định nghĩa là tỷ số giữa tốc độ ánh sáng trong chân không c và tốc độ pha vp trong vật liệu đó: chiết suất lớn hơn tương ứng với tốc độ ánh sáng trong vật liệu đó nhỏ hơn. Chiết suất của vật liệu có thể phụ thuộc vào tần số ánh sáng, cường độ, sự phân cực, hoặc hướng truyền sóng; tuy nhiên, trong nhiều trường hợp, tốc độ ánh sáng có thể coi là một hằng số cho từng vật liệu hay môi trường mà nó truyền qua. Ví dụ, chiết suất của không khí là khoảng 1,0003, trong khi các môi trường đặc hơn như nước, thủy tinh, và kim cương có chiết suất lần lượt là 1,3; 1,5 và 2,4 cho ánh sáng khả kiến. Trong các vật liệu như ngưng tụ Bose–Einstein gần nhiệt độ tuyệt đối không, tốc độ ánh sáng hiệu dụng chỉ là vài mét mỗi giây. Điều này là do ánh sáng (photon) bị trễ do hấp thụ và tái phát xạ bởi nguyên tử, dẫn đến tốc độ nhỏ hơn c trong môi trường. Do đó, ánh sáng có thể 'chạy chậm' trong vật chất, và hai nhóm nghiên cứu độc lập tuyên bố rằng họ đã làm cho ánh sáng gần như 'đứng yên' khi truyền qua ngưng tụ Bose–Einstein của nguyên tố rubidi. Một nhóm tại Đại học Harvard và Viện Khoa học Rowland ở Cambridge, Massachusetts, còn nhóm kia ở Trung tâm thiên văn vật lý Harvard–Smithsonian, cũng ở Cambridge. Tuy nhiên, mô tả phổ biến về ánh sáng 'đứng yên' trong các thí nghiệm này là ánh sáng chỉ được lưu trữ trong trạng thái kích thích của nguyên tử trong ngưng tụ Bose-Einstein, và sau đó nguyên tử phát ra photon vào một thời điểm bất kỳ sau đó, khi bị kích thích bởi xung laser. Trong thời gian mà các nhà vật lý gọi là 'đứng yên', ánh sáng không còn tồn tại dưới dạng ánh sáng nữa. Điều này nói chung đúng trong mọi môi trường trong suốt làm chậm ánh sáng khi nó truyền qua.
Trong vật liệu trong suốt, chiết suất thường lớn hơn 1, có nghĩa là tốc độ pha của sóng phải nhỏ hơn c. Trong một số vật liệu, chiết suất không thể nhỏ hơn 1 cho một số tần số; tuy nhiên, trong một số vật liệu nhân tạo, chiết suất có thể âm. Nguyên lý nhân quả không bị vi phạm, hàm ý rằng các phần thực và ảo của hằng số điện môi cho bất kỳ vật liệu nào, tương ứng với chiết suất và hệ số giảm yếu (attenuation coefficient), được mô tả trong liên hệ Kramers–Kronig. Trong thực tế, điều này có nghĩa là trong những vật liệu có chiết suất nhỏ hơn 1, sự hấp thụ sóng diễn ra rất nhanh đến mức không có tín hiệu nào có thể truyền nhanh hơn ánh sáng.
Khi một xung ánh sáng có tốc độ nhóm và tốc độ pha khác nhau (do tốc độ pha không đồng nhất đối với tất cả các tần số của xung), nó sẽ dần bị triệt tiêu theo thời gian, hiện tượng này được gọi là tán sắc quang học. Một số vật liệu có thể làm giảm tốc độ nhóm của sóng ánh sáng xuống cực thấp hoặc thậm chí bằng 0, tạo ra hiện tượng ánh sáng chậm (slow light), và điều này đã được xác nhận qua nhiều thí nghiệm. Ngược lại, có những vật liệu cho phép tốc độ nhóm của sóng vượt qua c trong các thí nghiệm. Tuy nhiên, tốc độ nhóm không thể đạt giá trị vô hạn hoặc âm, vì điều đó tương ứng với việc xung sẽ truyền ngay lập tức hoặc di chuyển ngược thời gian.
Dù vậy, không có trường hợp nào cho phép truyền thông tin vật lý nhanh hơn tốc độ ánh sáng c. Các nhà vật lý đã chứng minh rằng chúng ta không thể truyền thông tin bằng một xung ánh sáng có tốc độ vượt qua tốc độ của điểm đầu sóng (vận tốc đầu sóng). Dưới những điều kiện cụ thể, tốc độ đầu sóng luôn luôn bằng c.
Một hạt có khối lượng khi đi qua môi trường có thể có tốc độ lớn hơn tốc độ pha của xung ánh sáng trong môi trường đó (nhưng vẫn nhỏ hơn c). Khi một hạt mang điện tích di chuyển qua môi trường vật liệu có tính lưỡng cực điện, hạt đó sẽ phát ra sóng xung kích trong miền sóng điện từ, gọi là bức xạ Cherenkov.
Ảnh hưởng của tốc độ hữu hạn trong thực tiễn
Tốc độ ánh sáng liên quan trực tiếp đến khả năng truyền tin: Thời gian trễ trọn vòng và khoảng cách một chiều luôn lớn hơn 0. Độ trễ này có thể áp dụng cho các khoảng cách nhỏ đến những khoảng cách thiên văn. Mặt khác, một số kỹ thuật phụ thuộc vào tốc độ hữu hạn của ánh sáng, chẳng hạn như trong đo lường khoảng cách.
Khoảng cách ngắn
Trong các siêu máy tính, tốc độ ánh sáng quy định giới hạn tốc độ truyền dữ liệu giữa các bộ vi xử lý. Nếu một bộ vi xử lý hoạt động ở tần số 1 gigahertz, thì tín hiệu điện chỉ có thể di chuyển tối đa khoảng 30 cm (1 ft) trong một chu kỳ. Vì vậy, các bộ vi xử lý cần được đặt gần nhau để giảm thiểu độ trễ truyền tín hiệu; tuy nhiên, việc đặt chúng quá gần lại gây khó khăn trong việc tản nhiệt. Khi tần số đồng hồ tăng lên, tốc độ ánh sáng sẽ trở thành yếu tố giới hạn trong thiết kế kiến trúc mạch của từng con chip.
Khoảng cách lớn trên Trái Đất
Chu vi Trái Đất khoảng 40.075 km và tốc độ ánh sáng c vào khoảng 300.000 km/s, do đó thời gian ngắn nhất để một tín hiệu truyền qua nửa vòng Trái Đất là khoảng 67 milli giây. Khi ánh sáng truyền qua sợi quang, thời gian thực sẽ lâu hơn một chút vì ánh sáng di chuyển chậm hơn khoảng 35% so với tốc độ ánh sáng trong chân không, và phụ thuộc vào chiết suất của vật liệu n. Thêm vào đó, các tuyến cáp viễn thông ít khi thẳng tắp, do đó, độ trễ còn tăng thêm khi tín hiệu đi qua các bộ chuyển đổi điện tử hay các bộ bù suy giảm tín hiệu.
Chuyến bay không gian và thiên văn học

Việc truyền thông tin giữa Trái Đất và các tàu không gian không xảy ra ngay lập tức. Có một khoảng thời gian trễ từ lúc phát tín hiệu đến khi nhận được. Độ trễ này ảnh hưởng đáng kể đến việc liên lạc giữa Trung tâm điều khiển phi vụ và tàu Apollo 8, con tàu đầu tiên bay quanh Mặt Trăng: mỗi câu hỏi từ Trái Đất phải chờ ít nhất 3 giây mới nhận được trả lời từ phi hành gia. Đối với Sao Hỏa, độ trễ thông tin có thể dao động từ 5 đến 20 phút tùy thuộc vào vị trí của hai hành tinh. Vì vậy, nếu một robot trên bề mặt Sao Hỏa gặp phải chướng ngại vật, người điều khiển sẽ không biết ngay lập tức mà phải đợi ít nhất từ 5 đến 20 phút, và cần thêm thời gian tương tự để gửi lệnh từ Trái Đất đến Sao Hỏa. Do đó, các kỹ sư đã lập trình cho robot tự động phát hiện và xử lý chướng ngại vật.
NASA phải chờ vài giờ mới nhận được dữ liệu từ các tàu thăm dò Sao Mộc và Sao Thổ. Nếu cần điều chỉnh quỹ đạo của con tàu, tín hiệu điều chỉnh cũng mất thời gian tương ứng, điều này gây ra rủi ro trong việc điều khiển các tàu trong không gian sâu.
Ánh sáng và sóng điện từ từ các nguồn thiên thể xa xôi phải mất một khoảng thời gian dài mới đến Trái Đất. Ví dụ, ánh sáng từ những thiên hà xa nhất mất khoảng 12 tỷ năm để đến Trái Đất và được ghi lại trong bức ảnh chụp Vùng Sâu Hubble. Những bức ảnh này do kính thiên văn không gian Hubble chụp lại hình ảnh các thiên hà từ 12 tỷ năm trước, khi Vũ trụ mới chỉ hơn 1 tỷ năm tuổi. Nhờ vào sự hạn chế của tốc độ ánh sáng, các nhà thiên văn học có thể nghiên cứu sự tiến hóa của sao, thiên hà và cả Vũ trụ.
Khoảng cách trong thiên văn học thường được đo bằng năm ánh sáng, như thường thấy trong các ấn phẩm phổ biến hoặc trên các phương tiện truyền thông. Một năm ánh sáng tương đương với quãng đường mà ánh sáng di chuyển trong một năm, khoảng 9461 tỷ kilomet, hay 0,3066 parsec. Để đơn giản, một năm ánh sáng có thể được làm tròn thành 10 nghìn tỷ kilomet. Proxima Centauri, ngôi sao đỏ lùn gần Trái Đất nhất sau Mặt Trời, cách chúng ta khoảng 4,2 năm ánh sáng.
Đo khoảng cách
Bằng cách sử dụng radar, khoảng cách đến một vật thể có thể được xác định bằng cách đo thời gian mà xung vô tuyến quay trở lại ăng ten radar sau khi phản xạ từ vật thể cần đo: khoảng cách đến mục tiêu là nửa thời gian đo được nhân với tốc độ ánh sáng. Hệ thống GPS đo khoảng cách từ máy thu đến các vệ tinh GPS dựa trên thời gian tín hiệu vô tuyến cần để đến từng vệ tinh, từ đó tính toán tọa độ địa lý của máy thu. Vì tốc độ ánh sáng là khoảng 300.000 kilomet mỗi giây, nên việc đo thời gian và độ trễ giữa vệ tinh và máy thu cần phải cực kỳ chính xác. Các thí nghiệm như đo khoảng cách tới Mặt Trăng bằng laser, thiên văn vô tuyến, và Mạng lưới Không gian Sâu (Deep Space Network) đều có thể xác định khoảng cách đến Mặt Trăng, các hành tinh và tàu không gian bằng cách đo thời gian truyền tín hiệu vòng quanh.
Đo tốc độ ánh sáng
Có nhiều phương pháp để xác định giá trị của c. Một cách là đo trực tiếp tốc độ ánh sáng bằng cách quan sát trong nhiều thiên thể thiên văn học và trong phòng thí nghiệm. Tuy nhiên, có thể xác định gián tiếp giá trị của c thông qua các định luật vật lý mà hằng số này xuất hiện, chẳng hạn như đo hằng số điện môi ε0 và hằng số từ môi μ0, sau đó sử dụng các mối liên hệ giữa chúng để tính toán c. Lịch sử cho thấy, các kết quả chính xác nhất thường được thu thập từ việc đo riêng biệt tần số và bước sóng của chùm sáng đơn sắc, và nhân chúng lại để xác định giá trị của c.
Vào năm 1983, định nghĩa của đơn vị mét được cập nhật thành 'chiều dài ánh sáng truyền qua chân không trong khoảng thời gian 1⁄299.792.458 giây', và tốc độ ánh sáng được cố định chính xác ở mức 299792458 m/s, như được mô tả trong phần dưới. Do đó, những phép đo chính xác về tốc độ ánh sáng thực sự mang lại giá trị đo chính xác hơn cho c.
Trong thiên văn học
Không gian vũ trụ là một phòng thí nghiệm lý tưởng để đo tốc độ ánh sáng nhờ vào đặc tính chân không gần như hoàn hảo và không gian rộng lớn của nó. Các nhà thiên văn học thường đo thời gian ánh sáng cần thiết để đi qua những khoảng cách tham chiếu trong Hệ Mặt Trời, chẳng hạn như bán kính quỹ đạo của Trái Đất. Trong lịch sử, nhiều phép đo bán kính quỹ đạo đã đạt được độ chính xác cao dựa trên các đơn vị chiều dài được định nghĩa trước đó. Các kết quả thường được thể hiện bằng đơn vị thiên văn (AU) trên ngày. Một đơn vị thiên văn là khoảng cách trung bình từ Trái Đất đến Mặt Trời; nó không phải là đơn vị cơ bản trong hệ SI. Vì đơn vị AU được xác định dựa trên khoảng cách thực tế, nó không phải là cơ sở cho kỹ thuật đo thời gian bay như trong hệ SI, nhưng các phép đo hiện đại về tốc độ ánh sáng theo đơn vị thiên văn trên ngày có thể so sánh với định nghĩa của c trong hệ SI.
Ole Christensen Rømer là người đầu tiên sử dụng quan sát thiên văn học để ước lượng tốc độ ánh sáng. Khi đo từ Trái Đất, chu kỳ quỹ đạo của các vệ tinh tự nhiên quanh hành tinh xa sẽ thay đổi tùy thuộc vào khoảng cách từ Trái Đất: chu kỳ sẽ ngắn hơn khi hành tinh gần và dài hơn khi hành tinh xa. Khoảng cách ánh sáng phải truyền từ hành tinh (hoặc vệ tinh của nó) đến Trái Đất là ngắn nhất khi Trái Đất gần hành tinh và dài nhất khi Trái Đất xa hành tinh, sự chênh lệch giữa hai khoảng cách cực trị này bằng đường kính quỹ đạo Trái Đất quanh Mặt Trời. Rømer quan sát sự thay đổi trong chu kỳ quỹ đạo của vệ tinh Io của Sao Mộc và phát hiện ra rằng ánh sáng mất khoảng 22 phút để đi qua đường kính quỹ đạo Trái Đất (hiện tại giá trị đo được là hơn 16 phút).
Một phương pháp khác để xác định tốc độ ánh sáng là quan sát hiện tượng quang sai, được nhà thiên văn học James Bradley phát hiện và lý giải vào thế kỷ XVIII. Kết quả của phép đo này xuất phát từ việc cộng vectơ vận tốc của tia sáng phát ra từ nguồn xa (như ngôi sao) với vận tốc của thiết bị quan sát (xem hình bên). Một thiết bị quan sát đang di chuyển sẽ ghi nhận ánh sáng từ một hướng khác, dẫn đến sự dịch chuyển vị trí của nguồn sáng so với vị trí ban đầu. Do Trái Đất không ngừng quay và chuyển động trên quỹ đạo quanh Mặt Trời, hiệu ứng này gây ra hiện tượng các ngôi sao trên bầu trời di chuyển theo quỹ đạo tròn. Dựa vào góc lệch lớn nhất của các ngôi sao trên bầu trời (khoảng 20,5 giây cung), chúng ta có thể tính tốc độ ánh sáng bằng vận tốc của Trái Đất trên quỹ đạo quanh Mặt Trời, từ đó xác định thời gian ánh sáng cần để truyền từ Mặt Trời đến Trái Đất. Vào năm 1729, Bradley đã tính toán ánh sáng di chuyển nhanh hơn Trái Đất 10.210 lần trên quỹ đạo (so với 10.066 lần nhanh hơn theo tính toán hiện đại), tức là ánh sáng mất khoảng 8 phút 12 giây để đi từ Mặt Trời đến Trái Đất.
Hiện nay, giá trị 'thời gian ánh sáng cho đơn vị khoảng cách'—nghịch đảo của c, biểu thị bằng giây trên đơn vị thiên văn—được đo bằng cách so sánh thời gian tín hiệu vô tuyến đến các tàu không gian khác nhau trong hệ Mặt Trời, với vị trí của chúng được tính dựa trên hiệu ứng hấp dẫn từ Mặt Trời và các hành tinh khác. Kết hợp các quan sát này giúp chúng ta có giá trị chính xác nhất cho thời gian ánh sáng trên đơn vị khoảng cách. Tính đến năm 2009, giá trị chính xác nhất, được công nhận bởi Hiệp hội thiên văn quốc tế (IAU), là:
- Thời gian ánh sáng cho đơn vị khoảng cách: 499004783836(10) s
- c = 000200398880410(4) AU/s = 173144632674(3) AU/ngày
Sai số trong các phép đo hiện tại là 0,02 phần tỷ (2×10), tương đương với sai số trong việc đo khoảng cách bằng các giao thoa kế trên mặt đất. Kể từ khi mét được định nghĩa là chiều dài ánh sáng truyền qua chân không trong một khoảng thời gian nhất định, phép đo thời gian ánh sáng cho đơn vị khoảng cách cũng có thể được chuyển đổi sang độ dài của 1 AU bằng mét.
Kỹ thuật đo thời gian bay
Một phương pháp khác để đo tốc độ ánh sáng là đo thời gian ánh sáng di chuyển đến một gương ở khoảng cách xác định và phản xạ trở lại. Nguyên lý này được phát triển bởi Hippolyte Fizeau và Léon Foucault thông qua thiết bị được gọi là dụng cụ Fizeau–Foucault.
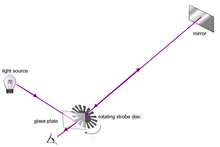
Fizeau thực hiện thí nghiệm bằng cách chiếu chùm sáng đến một gương phản xạ cách xa 8 kilômét (5 mi). Trên đường từ nguồn sáng đến gương, chùm sáng đi qua một bánh xe có răng. Khi bánh xe quay với tốc độ nhất định, chùm sáng đi qua khe răng cưa khi đến gương và phản xạ trở lại qua một khe khác; nếu bánh xe quay nhanh hoặc chậm hơn tốc độ đó, chùm sáng sẽ bị cản bởi răng và không thể xuyên qua. Khoảng cách đến bánh xe và gương đã được xác định trước; từ số răng trên bánh xe, tốc độ quay và khoảng cách đến gương, tốc độ ánh sáng có thể được tính toán.
Phương pháp của Foucault thay thế bánh xe răng cưa bằng một gương quay. Khi ánh sáng truyền từ nguồn đến gương phản xạ ở xa và quay trở lại, gương quay tạo ra sự thay đổi góc giữa tia tới và tia phản xạ. Từ góc thay đổi này, cùng với vận tốc quay đã biết và khoảng cách đến gương, Foucault đã tính toán được tốc độ ánh sáng.
Hiện nay, bằng cách sử dụng dao động ký với độ phân giải dưới một nanô giây, tốc độ ánh sáng có thể được đo trực tiếp bằng cách ghi lại độ trễ của chùm sáng hoặc laser từ một nguồn laser hoặc đèn LED phản xạ từ gương. Mặc dù phương pháp này có độ chính xác thấp hơn (với sai số khoảng 1%) so với các phương pháp hiện đại khác, nó vẫn thường được áp dụng trong các phòng thí nghiệm đại học.
Hằng số điện từ
Một phương pháp gián tiếp để xác định giá trị của c mà không cần đo sự lan truyền của sóng điện từ là sử dụng phương trình liên hệ giữa c với hằng số điện môi ε0 và hằng số từ môi μ0 trong lý thuyết Maxwell: c = 1/(ε0μ0). Hằng số điện môi được đo thông qua điện dung của một tụ điện với kích thước hình học đã biết, trong khi hằng số từ môi có giá trị cố định chính xác bằng 4π×10 H×m-1 theo định nghĩa đơn vị cường độ dòng điện Ampe. Rosa và Dorsey đã áp dụng phương pháp này vào năm 1907 và tính được giá trị 299710±22 km/s.
Sự cộng hưởng trong hốc
Một phương pháp khác để tính toán tốc độ ánh sáng là đo riêng biệt tần số f và bước sóng λ của sóng điện từ trong chân không. Từ đó, tốc độ ánh sáng c có thể được xác định dễ dàng bằng công thức c = fλ. Một phương pháp là sử dụng bộ cộng hưởng hốc (cavity resonator) để đo tần số cộng hưởng. Khi biết kích thước của hốc cộng hưởng, chúng ta có thể đo bước sóng của sóng vi ba. Năm 1946, Louis Essen và A.C. Gordon-Smith đo được tần số của nhiều mode chính tắc trong một hốc vi ba có kích thước chính xác. Kích thước của hốc được đo với sai số ±0,9μm bằng giao thoa kế. Sử dụng dữ liệu về bước sóng từ kích thước hốc và lý thuyết điện từ kết hợp với tần số đo được, họ đã tính được tốc độ ánh sáng.
Kết quả của nghiên cứu Essen–Gordon-Smith đạt được là 299792±9 km/s, chính xác hơn so với các kỹ thuật quang học trước đó. Đến năm 1950, các thí nghiệm lặp lại của Essen cung cấp giá trị 2997925±30 km/s.
Kỹ thuật này cũng có thể thực hiện tại nhà bằng lò vi sóng với thực phẩm như kẹo dẻo hoặc bơ thực vật: nếu đĩa xoay được nhấc ra, thực phẩm sẽ nóng nhất ở điểm bụng sóng (nơi sóng có biên độ lớn nhất), và bắt đầu chảy. Khoảng cách giữa hai điểm nóng nhất bằng một nửa bước sóng của sóng vi ba; đo khoảng cách này và nhân với tần số sóng vi ba (thường là 2450 MHz theo nhãn của lò), ta có thể tính được c với sai số thường dưới 5%.
Giao thoa kế
Giao thoa kế là thiết bị đo bước sóng của bức xạ điện từ và xác định tốc độ ánh sáng. Một chùm sáng kết hợp, như từ laser, với tần số đã biết (f), được chia thành hai tia rồi tái kết hợp. Bằng cách điều chỉnh quãng đường truyền của các tia sáng và cẩn thận đo quãng đường thay đổi, chúng ta có thể xác định bước sóng (λ). Tốc độ ánh sáng được tính bằng c = λf.
Trước khi có laser, các nguồn sóng vô tuyến đã được sử dụng để đo tốc độ ánh sáng qua giao thoa. Tuy nhiên, phương pháp giao thoa với sóng vô tuyến có độ chính xác thấp hơn và chỉ áp dụng cho bước sóng dài (~0,4 cm). Để cải thiện độ chính xác, có thể sử dụng ánh sáng có bước sóng ngắn hơn, nhưng việc đo trực tiếp tần số ánh sáng gặp khó khăn. Một giải pháp là bắt đầu với tín hiệu có tần số thấp đã biết và sau đó dùng các tín hiệu với tần số tăng dần có liên quan hoặc bội số của tần số ban đầu. Laser với tần số cố định và bước sóng đo được đã được nhóm tại Viện Tiêu chuẩn Quốc gia (NBS) (sau này là Viện Tiêu chuẩn và Công nghệ Quốc gia - NIST) thực hiện vào năm 1972 để đo tốc độ ánh sáng trong chân không với sai số 35×10.
Lịch sử
| 1675 | Rømer và Huygens, vệ tinh của Sao Mộc |
220000 |
| 1729 | James Bradley, hiện tượng quang sai |
301000 |
| 1849 | Hippolyte Fizeau, bánh răng quay |
315000 |
| 1862 | Léon Foucault, gương quay |
298 000±500 |
| 1907 | Rosa và Dorsey, hằng số EM |
299 710 ± 30 |
| 1926 | Albert Michelson, giao thoa kế |
299 796 ± 4 |
| 1950 | Essen và Gordon-Smith, bộ cộng hưởng hốc |
299 792,5 ± 3,0 |
| 1958 | K.D. Froome, giao thoa vô tuyến |
299 792,50 ± 0,10 |
| 1972 | Evenson, giao thoa kế laser |
299 792,4562 ± 0,0011 |
| 1983 | Phiên họp thứ 17 CGPM, định nghĩa lại đơn vị mét |
299 792,458 (chính xác) |
Đến thời kỳ cận đại, vẫn chưa rõ liệu ánh sáng di chuyển tức thời hay với tốc độ hữu hạn. Tranh luận về vấn đề này đã tồn tại từ thời Hy Lạp cổ đại. Các triết gia Hy Lạp cổ đại, Hồi giáo và châu Âu trung cổ đã tranh cãi về tốc độ ánh sáng cho đến khi Rømer thực hiện tính toán và quan sát đầu tiên. Thuyết tương đối hẹp của Einstein coi hằng số tốc độ ánh sáng là không đổi trong mọi hệ quy chiếu quán tính. Từ đó đến nay, các nhà khoa học đã thực hiện nhiều đo đạc để kiểm chứng tốc độ ánh sáng.
Lịch sử sơ khai
Empedocles là triết gia đầu tiên đề cập đến ý tưởng rằng tốc độ ánh sáng là hữu hạn. Ông cho rằng ánh sáng có chuyển động và cần thời gian để di chuyển một khoảng cách nhất định. Ngược lại, Aristotle tranh luận rằng 'ánh sáng là một thứ nhưng không di chuyển'. Euclid và Ptolemy phát triển lý thuyết về tầm nhìn của con người, cho rằng ánh sáng phát ra từ mắt và cho phép chúng ta thấy hình ảnh. Dựa trên lý thuyết này, Heron ở Alexandria cho rằng tốc độ ánh sáng phải vô hạn vì những vật thể xa như các ngôi sao hiện ra dường như ngay lập tức khi mắt mở ra.
Các triết gia Hồi giáo cổ đại ban đầu cũng đồng tình với Aristotle về việc ánh sáng không có tốc độ chuyển động. Năm 1021, Alhazen (Ibn al-Haytham) viết một cuốn sách về quang học, trong đó ông đưa ra nhiều lập luận về tầm nhìn và kết luận rằng ánh sáng phải phát ra từ vật để đến mắt người. Alhazen tin rằng ánh sáng di chuyển với tốc độ hữu hạn và giảm dần khi đi qua các vật liệu dày đặc hơn. Ông cũng cho rằng ánh sáng là một chất có thể truyền đi cần thời gian, dù chúng ta không luôn cảm nhận được. Cùng thời kỳ, Abū Rayhān al-Bīrūnī cũng đồng ý với quan điểm tốc độ ánh sáng là hữu hạn và nhận thấy ánh sáng có tốc độ nhanh hơn âm thanh.
Vào thế kỷ XIII, Roger Bacon đã cho rằng ánh sáng trong không khí không thể có tốc độ vô hạn, dựa trên lý thuyết của Alhazen và Aristotle. Trong thập niên 1270, Witelo đã khảo sát khả năng ánh sáng truyền với tốc độ vô hạn trong chân không nhưng chậm lại trong các môi trường khác.
Vào đầu thế kỷ XVII, nhà thiên văn học Johannes Kepler tin rằng tốc độ ánh sáng là vô hạn vì ông cho rằng trong chân không không có vật gì cản trở ánh sáng. René Descartes lập luận rằng nếu tốc độ ánh sáng là hữu hạn, Mặt Trời, Trái Đất, và Mặt Trăng có thể không còn sắp hàng trong hiện tượng nhật thực. Do không quan sát được sự lệch hàng này, Descartes kết luận rằng tốc độ ánh sáng là vô hạn. Ông cũng từng nói rằng nếu tốc độ ánh sáng được chứng minh là hữu hạn, toàn bộ lý thuyết triết học của ông sẽ bị sụp đổ.
Những nỗ lực đo đầu tiên
Vào năm 1629, Isaac Beeckman đã thiết lập một thí nghiệm trong đó một người quan sát ánh sáng phát ra từ nòng pháo, phản xạ từ một gương cách xa một dặm (1,6 km), nhưng không phát hiện ra sự chậm trễ. Đến năm 1638, Galileo Galilei đề xuất một thí nghiệm khác, có thể đã được suy nghĩ từ trước đó, để đo tốc độ ánh sáng bằng cách quan sát độ trễ khi mở và đóng một khe chắn sáng từ khoảng cách xa. Mặc dù ông không phân biệt được liệu ánh sáng truyền đi ngay lập tức hay không, nhưng ông kết luận rằng nếu tốc độ ánh sáng là hữu hạn, nó phải rất nhanh. Vào năm 1667, Galileo thực hiện thí nghiệm tại Accademia del Cimento ở Florence, Italia với đèn dầu cách xa một dặm, nhưng không phát hiện ra độ trễ. Độ trễ thực sự của thí nghiệm vào khoảng 11 micro giây và không thể nhận ra bằng mắt thường.

Ước tính đầu tiên về tốc độ ánh sáng được Rømer thực hiện vào năm 1676. Qua việc quan sát chu kỳ của vệ tinh Io của Sao Mộc, ông nhận thấy chu kỳ này giảm khi Trái Đất ở gần Sao Mộc và tăng khi Trái Đất xa Sao Mộc, từ đó ông kết luận rằng ánh sáng có tốc độ hữu hạn. Ông ước tính ánh sáng cần khoảng 22 phút để vượt qua đường kính quỹ đạo của Trái Đất. Nhà thiên văn học Christiaan Huygens đã kết hợp phương pháp này với tính toán quỹ đạo của Trái Đất để ước tính tốc độ ánh sáng là 220000 km/s, thấp hơn 26% so với giá trị thực tế.
Trong cuốn sách xuất bản năm 1704, Opticks, Isaac Newton đã đề cập đến các tính toán của Rømer về tốc độ hữu hạn của ánh sáng và tự tính toán thời gian ánh sáng mất để đi từ Mặt Trời đến Trái Đất khoảng '7 hoặc 8 phút' (giá trị hiện đại là 8 phút 19 giây). Newton cũng đặt câu hỏi liệu quan sát hiện tượng che khuất của Rømer có liên quan đến màu sắc hay không; và khi nhận thấy rằng các tính toán của Rømer không liên quan đến màu sắc, ông kết luận rằng tốc độ ánh sáng là như nhau cho tất cả các màu. Vào năm 1729, James Bradley phát hiện ra hiện tượng quang sai. Từ hiện tượng này, ông xác định rằng ánh sáng phải di chuyển nhanh hơn 10.210 lần so với tốc độ của Trái Đất trên quỹ đạo (giá trị hiện đại là 10.066), tương đương với thời gian ánh sáng mất khoảng 8 phút 12 giây để truyền từ Mặt Trời đến Trái Đất.
Liên hệ với lý thuyết điện từ
Vào thế kỷ XIX, Hippolyte Fizeau phát triển một phương pháp để đo tốc độ ánh sáng bằng cách đo thời gian ánh sáng di chuyển trên mặt đất và công bố giá trị 315000 km/s. Phương pháp của ông sau đó được Léon Foucault cải tiến, thu được giá trị 298000 km/s vào năm 1862. Năm 1856, Wilhelm Eduard Weber và Rudolf Kohlrausch đo tỷ số giữa đơn vị điện môi và đơn vị từ môi, 1/√ε0μ0, bằng cách sử dụng chai Leyden và thấy giá trị gần bằng với tốc độ ánh sáng mà Fizeau đã công bố. Về sau, Gustav Kirchhoff tính toán rằng tín hiệu điện truyền qua một dây lý tưởng không có điện trở di chuyển với tốc độ ánh sáng. Vào đầu những năm 1860, Maxwell chứng minh rằng theo lý thuyết điện từ của ông, sóng điện từ truyền trong chân không với vận tốc trùng với giá trị mà Weber/Kohlrausch đã tìm ra, và khi so sánh với giá trị tốc độ ánh sáng đo được của Fizeau, ông kết luận rằng ánh sáng thực chất là một dạng sóng điện từ.
'Ête siêu sáng'

Vào thế kỷ XIX, các nhà khoa học từng tin rằng chân không bị lấp đầy bởi một môi trường nền gọi là ête siêu sáng mà ánh sáng truyền qua. Một số nhà vật lý cho rằng ête này đóng vai trò như một hệ quy chiếu ưu tiên cho ánh sáng, từ đó có thể đo chuyển động của Trái Đất so với môi trường nền này bằng cách đo tính đẳng hướng của tốc độ ánh sáng. Vào đầu những năm 1880, nhiều người đã thử nghiệm để xác định chuyển động của Trái Đất so với ête, với thí nghiệm nổi tiếng nhất là của Albert Michelson và Edward Morley vào năm 1887. Kết quả cho thấy chuyển động luôn nhỏ hơn sai số thực nghiệm. Các thí nghiệm hiện đại hiện chỉ ra rằng giới hạn trên của chuyển động này - trong phương pháp hai đường truyền ánh sáng (two-way) về tính đẳng hướng của tốc độ ánh sáng (tốc độ bằng nhau ở mọi hướng) - phải nhỏ hơn 6 nanô mét trên giây. Hendrik Lorentz dựa trên kết quả thí nghiệm của Michelson để đưa ra giả thuyết rằng chuyển động của dụng cụ thí nghiệm trong môi trường ête làm co ngắn chiều dài theo hướng chuyển động, và ông còn giả định thêm rằng tốc độ thời gian trôi ('thời gian cục bộ') thay đổi theo công thức mà ông phát hiện, gọi là phép biến đổi Lorentz. Dựa trên lý thuyết ête của Lorentz, Henri Poincaré (1900) chứng minh rằng thời gian cục bộ (đối với số hạng bậc nhất v/c) đo bởi đồng hồ chuyển động trong ête, và đồng bộ hóa bởi tính hằng số của tốc độ ánh sáng. Năm 1904, ông dự đoán rằng tốc độ ánh sáng có thể giới hạn vận tốc của các hệ động lực, và các giả thuyết trong lý thuyết Lorentz đã được xác nhận. Đến năm 1905, Poincaré đã hoàn thiện lý thuyết ête của Lorentz thành lý thuyết hoàn toàn phù hợp với nguyên lý tương đối.
Thuyết tương đối hẹp
Vào năm 1905, Einstein đã đưa ra giả thuyết rằng tốc độ ánh sáng trong chân không, theo quan sát của một người không bị gia tốc, là không phụ thuộc vào chuyển động của nguồn sáng hoặc quan sát viên. Dựa trên tiên đề này và nguyên lý tương đối, ông đã phát triển thuyết tương đối hẹp, trong đó tốc độ ánh sáng trong chân không, ký hiệu c, được coi là một hằng số cơ bản và xuất hiện trong các phương trình không liên quan đến ánh sáng. Lý thuyết này đã làm cho khái niệm về môi trường ête tĩnh tại (trong lý thuyết Lorentz và phát triển bởi Poincaré) trở nên lỗi thời và cách mạng hóa cách hiểu của các nhà khoa học về không gian và thời gian.
Cải thiện độ chính xác của c và định nghĩa lại mét
Vào nửa sau thế kỷ XX, sự phát triển trong vật lý học và công nghệ đã giúp cải thiện độ chính xác của tốc độ ánh sáng. Đầu tiên, kỹ thuật đo bằng hốc cộng hưởng và sau đó là kỹ thuật giao thoa kế laser đã được áp dụng. Năm 1972, dựa trên phương pháp giao thoa kế laser và định nghĩa lại đơn vị đo mét từ năm 1960 theo vạch phổ của nguyên tử krypton-86, các nhà vật lý tại Viện Tiêu chuẩn và Công nghệ Quốc gia (NIST) ở Boulder, Colorado đã xác định tốc độ ánh sáng trong chân không là c = 2997924562±11 m/s. Giá trị này có sai số nhỏ hơn 100 lần so với các giá trị trước đó. Sai số trong phép đo chủ yếu đến từ độ bất định của định nghĩa đơn vị đo mét. Các thí nghiệm sau đó đã cho giá trị chính xác hơn cho c, và hội nghị Conférence Générale des Poids et Mesures (CGPM) lần thứ 15 năm 1975 đã đề xuất sử dụng giá trị 299792458 m/s cho tốc độ ánh sáng.
Năm 1983, hội nghị CGPM lần thứ 17 đã định nghĩa lại đơn vị đo mét, quy định rằng 'Mét là độ dài quãng đường ánh sáng truyền trong chân không trong khoảng thời gian bằng 1/299 792 458 của một giây.' Theo định nghĩa này, tốc độ ánh sáng trong chân không chính xác là 299792458 m/s và đã trở thành một hằng số được định nghĩa trong hệ đơn vị SI. Các thí nghiệm nâng cao độ chính xác không thay đổi giá trị của tốc độ ánh sáng trong hệ SI, thay vào đó giúp đo chính xác hơn đơn vị mét.
- Thuyết điện từ học
- Quang học
- Thuyết tương đối
- Ánh sáng
Ghi chú
Tham khảo thêm
- Rømer, O (1676). “Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences”. Journal des sçavans (bằng tiếng Pháp): 223–36. Bản gốc lưu trữ ngày 29 tháng 7 năm 2007. Truy cập ngày 3 tháng 4 năm 2013.
- Được dịch là “A Demonstration concerning the Motion of Light”. Philosophical Transactions of the Royal Society (136): 893–4. 1677. Bản gốc lưu trữ ngày 29 tháng 7 năm 2007. Truy cập ngày 3 tháng 4 năm 2013.
- Halley, E (1694). “Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London”. Philosophical Transactions of the Royal Society. 18 (214): 237–56. doi:10.1098/rstl.1694.0048.
- Fizeau, HL (1849). “Sur une expérience relative à la vitesse de propagation de la lumière” (PDF). Comptes rendus de l'Académie des sciences (bằng tiếng Pháp). 29: 90–92, 132. Bản gốc (PDF) lưu trữ ngày 13 tháng 6 năm 2011. Truy cập ngày 3 tháng 4 năm 2013.
- Foucault, JL (1862). “Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil”. Comptes rendus de l'Académie des sciences (bằng tiếng Pháp). 55: 501–503, 792–796.
- Michelson, AA (1878). “Experimental Determination of the Velocity of Light”. Proceedings of the American Association of Advanced Science. 27: 71–77.
- Michelson, AA; Pease, FG; Pearson, F (1935). “Measurement of the Velocity of Light in a Partial Vacuum”. Astrophysical Journal. 82: 26–61. Bibcode:1935ApJ....82...26M. doi:10.1086/143655.
- Newcomb, S (1886). “The Velocity of Light”. Nature. 34 (863): 29–32. Bibcode:1886Natur..34...29.. doi:10.1038/034029c0.
- Perrotin, J (1900). “Sur la vitesse de la lumière”. Comptes rendus de l'Académie des sciences (bằng tiếng Pháp). 131: 731–4.
- Brillouin, L (1960). Wave propagation and group velocity. Academic Press.
- Jackson, JD (1975). Classical Electrodynamics (ấn bản 2). John Wiley & Sons. ISBN 0-471-30932-X.
- Keiser, G (2000). Optical Fiber Communications (ấn bản 3). McGraw-Hill. tr. 32. ISBN 0-07-232101-6.
- Ng, YJ (2004). “Quantum Foam and Quantum Gravity Phenomenology”. Trong Amelino-Camelia, G; Kowalski-Glikman, J (biên tập). Planck Scale Effects in Astrophysics and Cosmology. Springer. tr. 321ff. ISBN 3-540-25263-0.Quản lý CS1: nhiều tên: danh sách biên tập viên (liên kết)
- Helmcke, J; Riehle, F (2001). “Physics behind the definition of the meter”. Trong Quinn, TJ; Leschiutta, S; Tavella, P (biên tập). Recent advances in metrology and fundamental constants. IOS Press. tr. 453. ISBN 1-58603-167-8.Quản lý CS1: nhiều tên: danh sách biên tập viên (liên kết)
- Duff, MJ (2004). 'Comment on time-variation of fundamental constants'. arΧiv:hep-th/0208093 [hep-th].
Liên kết bên ngoài
 Cổng thông tin về Sao
Cổng thông tin về Sao Cổng thông tin về Thiên văn học
Cổng thông tin về Thiên văn học- Tốc độ ánh sáng theo Từ điển bách khoa Việt Nam
- Speed of light trên Encyclopædia Britannica (tiếng Anh)
- 'Kiểm tra tốc độ ánh sáng trong ống chân không dài một dặm.' Popular Science Monthly, tháng 9 năm 1930, trang 17–18.
- Tốc độ ánh sáng trong chân không (Viện Tiêu chuẩn và Công nghệ Quốc gia, NIST)
- Định nghĩa về mét (Cục Đo lường Quốc tế, BIPM)
- Thư viện dữ liệu: Tốc độ ánh sáng Michelson (Đánh giá vị trí đơn biến) (tải dữ liệu thu thập bởi A.A. Michelson)
- Subluminal Lưu trữ 2005-06-15 tại Wayback Machine (Java applet minh họa giới hạn thông tin vận tốc nhóm)
- De Mora Luminis tại MathPages
- Thảo luận về ánh sáng và cộng dồn vận tốc
- Tốc độ ánh sáng Lưu trữ 2008-01-15 tại Wayback Machine (Khoa Vật lý, Đại học Colorado)
- c: Tốc độ ánh sáng (Sixty Symbols, Khoa Vật lý Đại học Nottingham [video])
- FAQ Vật lý Usenet
- Phương pháp 'Bánh răng xoay nhanh' của Fizeau Lưu trữ 2010-04-11 tại Wayback Machine
| Tiêu đề chuẩn |
|
|---|

Thuyết tương đối |
|---|
Kỷ lục | |||||||
|---|---|---|---|---|---|---|---|
| Kỷ lục |
| ||||||
| Người |
| ||||||
| Kỷ lục thể thao |
| ||||||
| Kỷ lục quốc tế |
| ||||||
| Motion records |
| ||||||
| Man-made objects |
| ||||||
| Physical phenomena |
| ||||||
Thiên văn học sóng hấp dẫn |
|---|
