1. Kiến thức cơ bản liên quan:
1.1 Hình vuông
- Hình vuông là một tứ giác với bốn góc vuông và bốn cạnh bằng nhau. Nó kết hợp tất cả các đặc điểm của hình thoi, hình thang và hình chữ nhật. Hình vuông có bốn góc vuông, hai đường chéo cắt nhau vuông góc và hai cặp cạnh đối diện song song.
- Nhận xét:
+ Hình vuông là một loại hình chữ nhật với tất cả bốn cạnh bằng nhau
+ Hình vuông cũng là một hình thoi với tất cả các góc đều vuông.
+ Hình vuông kết hợp đặc điểm của cả hình chữ nhật và hình thoi.
- Các đặc điểm của hình vuông:
+ Hình vuông có hai đường chéo cắt nhau vuông góc tại trung điểm của mỗi đường và có chiều dài bằng nhau.
+ Hình vuông có hai cặp cạnh song song với nhau.
+ Tổng của bốn góc trong hình vuông là 360 độ, mỗi góc bằng 90 độ.
+ Hình vuông có một đường tròn nội tiếp và một đường tròn ngoại tiếp, với tâm của cả hai trùng nhau tại giao điểm của hai đường chéo.
+ Một đường chéo chia hình vuông thành hai phần có diện tích bằng nhau.
+ Tất cả các đường phân giác, trung tuyến và trung trực của hình vuông đều cắt nhau tại một điểm duy nhất.
- Cách nhận diện hình vuông:
+ Nếu một hình chữ nhật có hai cạnh kề bằng nhau, đó là hình vuông.
+ Nếu một hình chữ nhật có hai đường chéo vuông góc với nhau, đó là hình vuông.
+ Nếu một hình chữ nhật có một đường chéo là đường phân giác của một góc, thì đó là hình vuông.
+ Nếu hình thoi có một góc vuông thì đó là hình vuông.
+ Nếu hình thoi có hai đường chéo bằng nhau, thì đó là hình vuông.
- LƯU Ý: Một tứ giác vừa là hình chữ nhật vừa là hình thoi thì đó là hình vuông.
- Công thức tính chu vi hình vuông: P = a x 4
- a: độ dài của một cạnh
- P: chu vi
- Công thức tính diện tích hình vuông: S = a x a
- a: độ dài của một cạnh
- S: diện tích
* Bài thơ về cách tính chu vi và diện tích hình vuông:
Để tính diện tích hình vuông
Cạnh nhân chính nó là công thức đơn giản.
Cách tính chu vi hình vuông là như thế này
Chỉ cần nhân chiều dài một cạnh với bốn là ra ngay!
- Các dạng bài tập liên quan đến tính diện tích hình vuông:
+ Dạng 1: Biết độ dài cạnh, tính diện tích của hình vuông.
+ Dạng 2: Biết diện tích hình vuông, tìm độ dài của cạnh.
+ Dạng 3: Tính chu vi hình vuông khi đã biết diện tích của nó.
+ Dạng 4: Tính diện tích hình vuông khi biết chu vi của nó.
1.2 Hình chữ nhật
- Hình chữ nhật là một tứ giác với bốn góc vuông.
- Các đặc điểm nhận biết hình chữ nhật:
+ Tứ giác có ba góc vuông.
+ Hình thang cân có một góc vuông.
+ Hình bình hành có một góc vuông.
+ Hình bình hành có hai đường chéo bằng nhau.
- Các đặc điểm của hình chữ nhật:
+ Hình chữ nhật có đầy đủ các đặc điểm của hình bình hành và hình thang cân.
+ Trong hình chữ nhật, hai đường chéo đều bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Công thức tính chu vi hình chữ nhật: P = 2 x (a + b)
- a: chiều dài
- b: chiều rộng
- P: Chu vi
- Công thức tính diện tích hình chữ nhật: S = a x b
- a: chiều dài
- b: chiều rộng
- S: diện tích
- Các bài toán thường gặp:
+ Tính diện tích hình chữ nhật khi đã biết chiều dài và chiều rộng.
+ Tính diện tích của hình khi có nhiều hình chữ nhật ghép lại.
+ Xác định chiều dài và chiều rộng khi đã biết diện tích và một cạnh của hình chữ nhật.
* Bài thơ về chu vi và diện tích hình chữ nhật:
Chu vi của chữ nhật sao cho dễ?
Tính tổng dài và rộng rồi nhân đôi ngay!
Diện tích của chữ nhật dễ thôi,
Chỉ cần nhân dài với rộng là xong, điểm mười sẽ đến!
1.3 Hình thang
- Hình thang là một tứ giác lồi với hai cạnh đối diện song song, gọi là các cạnh đáy. Hai cạnh còn lại gọi là các cạnh bên.
- Cấu trúc:
Hình thang ABCD bao gồm:
- Cạnh đáy AB và cạnh đáy DC, cùng với hai cạnh bên AD và BC.
- Hai cạnh đáy là các cạnh đối diện và song song với nhau.
- Hình thang có một cặp cạnh đối diện là song song.
CHÚ Ý: Nếu một cạnh bên của hình thang vuông góc với cả hai đáy thì hình thang đó gọi là hình thang vuông.
.png)
- Đường cao của hình thang
AH là đường cao, với độ dài AH là chiều cao. Tương tự, AD cũng là đường cao và độ dài của AD là chiều cao.
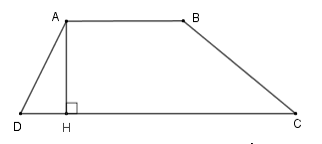
.png)
- Cách nhận diện hình thang:
+ Tứ giác với hai cạnh đối song song.
+ Hình thang với một góc vuông được gọi là hình thang vuông.
+ Hình thang có hai góc kề một đáy là hình thang cân.
+ Hình thang với hai cạnh bên bằng nhau là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Các dạng đặc biệt của hình thang:
+ Hình thang vuông: hình thang với một góc vuông.
+ Hình thang cân: hình thang với hai góc kề một đáy bằng nhau.
+ Hình bình hành: hình thang với hai đáy và hai cạnh bên đều bằng nhau, và song song.
- Chu vi của hình thang: P = a + b + c + d
- a và b là chiều dài của hai đáy
- c và d là chiều dài của hai cạnh bên
- P: Chu vi
- Công thức tính diện tích hình thang: S = (a + b) x h : 2
- a & b: chiều dài đáy lớn và đáy nhỏ
- h: chiều cao
- S: diện tích
* Bài thơ về diện tích hình thang:
Để tính diện tích hình thang
Cộng đáy dài với đáy ngắn
Nhân với chiều cao để tính diện tích
Chia đôi kết quả để có diện tích cuối cùng
1.4. Hình tam giác
Hình tam giác ABC có:
- Ba cạnh: AB, AC, BC
- Ba đỉnh: A, B, C
- Ba góc:
+ Góc tại A, giữa cạnh AB và AC - góc A
+ Góc tại B, giữa cạnh BA và BC - góc B
+ Góc tại C, giữa cạnh AC và CB - góc C
.png)
- Chu vi của hình tam giác: C = a + b + c
- a, b, c là độ dài của ba cạnh hình tam giác
- Diện tích hình tam giác: S = a x h / 2
- a: độ dài đáy
- h: chiều cao
- Trường hợp đặc biệt:
+ Diện tích của tam giác vuông: S = a x b / 2
- a: độ dài cạnh vuông góc thứ nhất
- b: độ dài cạnh vuông góc thứ hai
* Bài thơ về diện tích của tam giác và tam giác vuông:
- Diện tích của tam giác thông thường:
Tính diện tích tam giác không khó đâu
Nhân chiều cao với đáy rồi chia đôi là xong.
- Diện tích của tam giác vuông:
Tam giác có hai cạnh vuông góc
Bình tĩnh đừng lo lắng, sai là do vội vàng.
Nhân hai cạnh với nhau rồi chia đôi
Sẽ có diện tích, làm bài nhanh chóng thôi.
2. Hướng dẫn giải bài tập Toán lớp 5 bài 102
Bài 1:
Phương pháp giải
- Chia khu đất thành một hình vuông (1) và hai hình chữ nhật (2) và (3) như trong hình.
.png)
Diện tích khu đất là tổng của diện tích hình vuông (1) và hai hình chữ nhật (2) và (3).
Bài giải
Diện tích hình vuông (1):
5 x 5 = 25 (m2)
Chiều dài hình chữ nhật (2):
6 + 5 = 11 (m)
Diện tích hình chữ nhật (2):
6 x 11 = 66 (m2)
Chiều dài hình chữ nhật (3):
7 + 6 + 5 = 18 (m)
Chiều rộng hình chữ nhật (3):
16 - 6 - 7 = 5 (m)
Diện tích hình chữ nhật (3):
18 x 5 = 90 (m2)
Diện tích khu đất:
25 + 66 + 90 = 181 (m2)
Kết quả: 181 m2
Bài 2:
Phương pháp giải
- Chia khu đất thành các hình: tam giác ABM, hình thang BCMN, tam giác CND, và tam giác ADE như trong hình.
- Theo đề bài: BM = 14m, CN = 17m
AM = 12m, MN = 15m
EP = 20m, ND = 31m
.png)
- Tổng diện tích khu đất là tổng của diện tích tất cả các hình.
Bài giải
Diện tích tam giác ABM:
12 x 14 : 2 = 84 (m2)
Diện tích hình thang BCNM:
(14 + 17) x 15 : 2 = 232,5 (m2)
Diện tích tam giác CND:
31 x 17 : 2 = 263,5 (m2)
Chiều dài cạnh AD:
12 + 15 + 31 = 58 (m)
Diện tích tam giác ADE:
20 x 58 : 2 = 580 (m2)
Tổng diện tích khu đất:
84 + 232,5 + 263,5 + 580 = 1160 (m2)
Kết quả: 1160 (m2)
Mytour hy vọng cung cấp cho quý khách thông tin tư vấn hữu ích. Tham khảo: Công thức tính diện tích hình bình hành chính xác và bài tập kèm theo. Xin chân thành cảm ơn sự hợp tác của quý khách hàng!
