1. Những kiến thức lý thuyết cần nắm
Cách tìm giá trị m để bất phương trình có nghiệm
Phương pháp: Để giải các bài toán xác định điều kiện cho bất phương trình có nghiệm với mọi x hoặc bất phương trình không có nghiệm, chúng ta sử dụng những lập luận sau đây:
Xem xét bất phương trình bậc hai với một ẩn
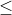
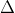
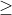
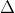

Ví dụ: Xét bất phương trình (m - 1)x2 + 2mx - 3 > 0. Tìm giá trị của m sao cho bất phương trình có nghiệm với mọi x thuộc R.
Hướng dẫn giải quyết:
Xét hàm số (m - 1) x2 + 2mx - 3 = f(x)
Trường hợp 1: m - 1 = 0
2. Xác định giá trị m để bất phương trình có nghiệm
Ví dụ 1: Xét bất phương trình (m - 1) x2 + 2mx - 3 > 0. Tìm giá trị của m để bất phương trình luôn có nghiệm với mọi x thuộc R.
Hướng dẫn giải quyết
Xét hàm số (m - 1) x2 + 2mx - 3 = f(x)
Trường hợp 1: m - 1 = 0 ⇒ m = 1. Thay m = 1 vào bất phương trình ta có: 2x - 3 > 0 ⇒ x > 3/2 (không có nghiệm)
Trường hợp 2: m - 1 ≠ 0 ⇔ m ≠ 1
⇔ m - 1 > 0; 4m2 + 12m - 12 < 0
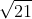
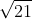
⇔ m thuộc tập rỗng
Do đó, không có giá trị nào của m để bất phương trình có nghiệm với mọi x thuộc R.
2. Xác định giá trị m để bất phương trình có nghiệm với đáp án chi tiết
Câu 1: Xác định m để bất phương trình x2 - 2(m + 1) + m2 + 2m < 0 có nghiệm cho mọi x thuộc khoảng [0; 1]
Hướng dẫn giải
Xét bất phương trình x2 - 2(m + 1) + m2 + 2m < 0
Do đó, bất phương trình có nghiệm cho mọi x trong khoảng [0; 1]
Hàm số f(x) = 0 có nghiệm thỏa mãn điều kiện trên
x1 < 1 < 2 < x2
⇔ kf(0) < 0 ; kf(0) < 0
⇔ m2 + 2m < 0 ; m2 - 1 < 0
⇔ -1 < m < 0
Vậy giá trị m trong khoảng -1 < m < 0 sẽ thỏa mãn yêu cầu bài toán
Câu 2: Xác định giá trị của m để bất phương trình (m + 2) x2 - 2mx + m2 + 2m < 0 có nghiệm
Hướng dẫn giải
Xem xét 3 trường hợp khác nhau:
Trường hợp 1: Nếu m + 2 = 0 thì m = -2, ta có:
(1) 4x + 4 < 0 ⟹ x < -1
Bất phương trình không có nghiệm
Trường hợp 2: Khi m < -2
Bất phương trình đã cho vẫn có nghiệm
Trường hợp 3: Nếu m + 2 > 0 thì m > -2
Trong trường hợp này, bất phương trình sẽ có nghiệm nếu vế trái có hai nghiệm phân biệt
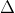
⇔ m^2 - 2 > 0
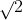
Câu 3: Xác định giá trị của m để bất phương trình m^2x + 3 < mx + 4 có nghiệm.
Hướng dẫn giải:
Bất phương trình tương đương với: m^2x - mx < 4
⇔ (m^2 - m)x < 1
m^2 - m = 0
m = {0; 1}
khi đó bất phương trình trở thành 0 < 1, điều này đúng với mọi giá trị x
Do vậy, bất phương trình có vô số nghiệm
Khi m^2 - m ≠ 0
nếu m ≠ {0; 1}, bất phương trình trở thành x < 1/(m^2 - m), do đó luôn có nghiệm x < 1/(m^2 - m)
Vậy bất phương trình sẽ có nghiệm cho mọi giá trị thực của m
Câu 4: Xác định m sao cho bất phương trình m^2x + 3 < mx + 4 có nghiệm
Hướng dẫn giải:
Bất phương trình có thể viết lại như sau:
m^2x - mx < 1
(m^2 - m)x < 1
Khi m^2 - m = 0
m = {0; 1}
thì bất phương trình trở thành 0 < 1, điều này đúng với mọi giá trị x
Do đó, bất phương trình có vô số nghiệm
Khi m^2 - m = 0 và m khác 0
m khác {0; 1}
thì bất phương trình trở thành x < 1/(m^2 - m)
Câu 5: Xác định giá trị của m để bất phương trình (m + 4)x^2 - 2mx + 2m - 6 < 0 có nghiệm với mọi x
Hướng dẫn giải
Khi m = -4, bất phương trình trở thành: 8x - 14 < 0 với mọi x (loại)
Khi m khác -4, f(x) < 0 với mọi x
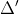
⇔ m < -4 và m^2 - (m + 4)(2m - 6) < 0
⇔ m < -4
m < -4
Do đó, bất phương trình có nghiệm đúng với mọi x khi m < -4.
3. Bài tập ứng dụng để tìm m sao cho bất phương trình có nghiệm
Câu 1: Xét đa thức f(x) = x^2 - 2mx + 3m - 2. Xác định điều kiện của m để f(x) > 0 với mọi x thuộc [1 ; 2]
Câu 2: Tìm giá trị của m để với mọi x đều thỏa mãn: mx^2 - 4x + 3m + 1 > 0
Câu 3: Tìm giá trị của m sao cho bất phương trình x^2 - 2x + 1 - m^2 < 0 có nghiệm với mọi x thuộc khoảng [1 ; 2]
Câu 4: Tìm giá trị của m để bất phương trình sau có nghiệm với mọi x thuộc khoảng (-1 ; 3):
3 (m - 2) x^2 + 2 (m + 1) x + m - 1 < 0
Câu 5: Xác định m để bất phương trình m^2 - 2mx + 4 > 0 có nghiệm với mọi m thuộc khoảng (-1 ; 0,5)
Câu 6: Tìm điều kiện của m để tất cả nghiệm của bất phương trình x^2 + (m - 1)x - m < 0 đều thỏa mãn bất phương trình này
Câu 7: Xác định giá trị của m để bất phương trình (m - 2) x^2 + 2mx - 2 - m < 0 có nghiệm
Câu 8: Tìm giá trị của tham số m khác 0 sao cho bất phương trình f(x) = 2mx^2 - (1 - 5m)x + 3m + 1 > 0 có nghiệm với mọi x thuộc khoảng (-2 ; 0)
Câu 9: Tìm giá trị của m để bất phương trình sau có nghiệm với mọi x thuộc R:
(m - 5) x^2 - 2x + m + 1 > 0
Câu 10: Tìm giá trị của tham số m sao cho bất phương trình sau luôn có nghiệm đúng với mọi x
a. 5x^2 - x + m > 0
b. mx^2 - 10x - 5 < 0
c. m (m + 2) x^2 - 2mx + 2 > 0
d. (m + 1) x^2 - 2(m - 1)x + 3m - 3 < 0
Câu 11: Xác định m để bất phương trình dưới đây có nghiệm với mọi x thuộc R
2mx^2 + 2(m - 1)x + 7m + 9 / (x^2 + 1) > 1
Câu 12: Tìm m sao cho các bất phương trình sau có nghiệm với mọi x
a. x^2 - 2(m - 2)x + 2(m^2 - 2x + 3) > 0
b. mx^2 + (m - 1)x + m - 1 < 0
Câu 13: Xác định m để đa thức (3m + 1)x^2 - (3m + 1)x + m + 4 luôn dương với mọi x
Câu 14: Tìm m để phương trình: (m^2 + m + 1)x^2 + (2m - 3)x + m - 5 = 0 có hai nghiệm dương và phân biệt
Câu 15: Tìm m sao cho các bất phương trình sau có nghiệm với mọi x
a. 3x^2 + 2(m - 1)x + m + 4 > 0
b. x^2 + (m + 1)x + 2m + 7 > 0
c. 2x^2 + (m - 2)x - m + 4 > 0
Câu 16: Xác định giá trị của m để các phương trình dưới đây có nghiệm
a. (m - 5)x^2 - 4mx + m - 2 = 0
b. (m - 2)x^2 + 2(2m - 3)x + 5m - 6 = 0
Bài viết trên Mytour đã cung cấp thông tin chi tiết về việc tìm m sao cho bất phương trình có nghiệm, bao gồm cách giải và bài tập tự luyện thêm. Cảm ơn các bạn đã theo dõi bài viết.
