1. Khái niệm về hàm số đồng biến và nghịch biến
Hàm số là một mối liên hệ giữa các phần tử trong tập hợp x với một phần tử trong tập hợp Y.
Hàm số đồng biến là hàm số mà khi x tăng hoặc giảm thì f(x) cũng tăng hoặc giảm theo. Ngược lại, hàm số nghịch biến là hàm số mà khi x tăng thì f(x) giảm, và khi x giảm thì f(x) tăng.
Đồng biến và nghịch biến là hai thuộc tính quan trọng của hàm số. Một hàm số được gọi là đơn điệu trong một khoảng nếu nó tăng hoặc giảm đều đặn trong khoảng đó. Nếu sự thay đổi là nghiêm ngặt, tức là hàm số tăng hoặc giảm một cách rõ ràng, thì được gọi là đơn điệu nghiêm ngặt. Để xác định tính chất đơn điệu, người ta thường tìm đạo hàm của hàm số. Nếu đạo hàm lớn hơn hoặc bằng 0, hàm số là đồng biến; nếu nhỏ hơn hoặc bằng 0, hàm số là nghịch biến.
2. Xác định giá trị m để hàm số đồng biến hoặc nghịch biến trên một khoảng
- Phương pháp giải bài tập tìm m để hàm số đồng biến hoặc nghịch biến trên R
Bước 1: Tính đạo hàm y'. Nếu y' lớn hơn hoặc bằng 0, hàm số đồng biến trên R; nếu y' nhỏ hơn hoặc bằng 0, hàm số nghịch biến trên R.
Bước 2: Thông thường, y' là một tam thức bậc hai, vì vậy cần dựa vào các nhận xét để xác định giá trị m.
2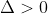 2
2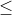
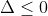
Đạo hàm y' = x2 - 4x + m - 2020
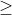 2
2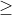
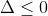
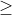
- Phương pháp giải bài toán tìm giá trị m để hàm số đồng biến hoặc nghịch biến trên một khoảng K, là tập con của R.
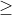
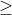
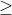
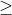
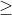
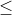
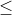
Ví dụ cụ thể: Xác định tất cả các giá trị của tham số m sao cho hàm số f(x) = x3 - 3mx2 + 3 (2m -1)x đồng biến trên khoảng (2;3)
2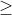 2
2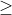
 2
2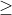 2
2Lưu ý rằng với mọi x thuộc khoảng (2;3), ta có 2 - 2x < 0, vì vậy:
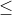 2
2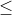

3. Phương pháp hiệu quả để học tốt chủ đề hàm số trong chương trình toán phổ thông
Chủ đề hàm số là một phần quan trọng và thú vị trong chương trình học phổ thông. Đây được coi là một trong những phần khó nhất của toán học phổ thông. Nhiều câu hỏi khó trong các kỳ thi thường liên quan đến chủ đề này. Để học tốt và cải thiện điểm số, học sinh cần chú trọng đến chủ đề này vì nó xuất hiện ở mọi mức độ từ nhận biết đến vận dụng cao. Dưới đây là một số lưu ý để học tốt chủ đề hàm số trong chương trình toán học phổ thông:
- Nắm vững kiến thức cơ bản là điều tiên quyết. Để học tốt bất kỳ chủ đề nào trong toán học, bạn cần hiểu rõ các kiến thức cơ bản. Việc này không hề dễ dàng và cần thời gian. Hãy lắng nghe kỹ các bài giảng từ giáo viên, tham khảo sách giáo khoa và sách bổ trợ, hoặc tham gia các lớp học thêm nếu cần. Ngoài việc ghi nhớ, thực hành thường xuyên là rất quan trọng. Đừng chỉ học lý thuyết, hãy áp dụng vào bài tập để nâng cao kỹ năng giải quyết vấn đề.
- Phát triển kỹ năng suy luận. Toán học yêu cầu khả năng suy luận logic và kết nối các kiến thức từ nhiều chủ đề khác nhau. Học toán không chỉ là học thuộc, mà còn cần phải giải quyết bài toán bằng nhiều phương pháp khác nhau. Hãy học cách phân tích bài toán và sử dụng dữ liệu để giải quyết vấn đề một cách hiệu quả. Khả năng suy luận giúp bạn giải quyết các bài toán khó và thay đổi cách ra đề.
- Khi gặp bài tập hàm số, hãy sắp xếp kiến thức cơ bản và các phương pháp giải bài. Thực hiện từng bước một cách cẩn thận. Đừng vội vàng hay cố gắng làm nhanh nếu chưa thành thạo dạng bài. Ban đầu, hãy tập trung vào chất lượng và sau đó nâng cao tốc độ làm bài để xử lý nhiều câu hỏi hơn. Luyện tập nhiều loại bài tập trong cùng một chủ đề sẽ giúp bạn ghi nhớ và tránh nhầm lẫn.
Toán học không thể học theo kiểu ghi nhớ máy móc. Nó đòi hỏi tư duy, sự chăm chỉ và khám phá. Hãy học toán một cách thoải mái, không quá lo lắng về điểm số. Tập trung vào việc hiểu bản chất và tự nghiên cứu các dạng bài mới. Tư duy là cần thiết nhưng không đủ, bạn cũng cần nỗ lực và rèn luyện liên tục. Đối mặt với khó khăn và cố gắng, bạn sẽ cải thiện điểm số môn toán hiệu quả.
