Xác định m để bài toán bất phương trình không có nghiệm kèm theo các bài tập và đáp án chi tiết

1. Bất phương trình và các khái niệm cơ bản

1.1. Định nghĩa về bất phương trình

Bất phương trình là một mệnh đề thể hiện mối quan hệ giữa hai biểu thức, trong đó ít nhất một biểu thức có chứa một dấu bất đẳng thức (dấu '>' - lớn hơn, '<' - nhỏ hơn, '>=' - lớn hơn hoặc bằng, '<=' - nhỏ hơn hoặc bằng, hoặc '≠' - khác nhau). Bất phương trình chỉ ra mối quan hệ giữa giá trị của các biểu thức và xác định các giá trị của biến để bất phương trình trở nên đúng.

Ví dụ minh họa về bất phương trình:

VD1: 2x + 5 > 10. Đây là một bất phương trình với biến x, chỉ ra rằng giá trị của biểu thức 2x + 5 phải lớn hơn 10. Để giải bài toán này, ta cần xác định các giá trị của x sao cho biểu thức 2x + 5 lớn hơn 10.

VD2: y² ≤ 25. Đây là một bất phương trình với biến y, cho biết rằng giá trị của biểu thức y² không vượt quá 25. Để giải bài toán này, ta cần tìm các giá trị của y sao cho biểu thức y² nhỏ hơn hoặc bằng 25.

Các ký hiệu trong bất phương trình có thể khác nhau tùy thuộc vào loại bất phương trình và điều kiện của biểu thức. Khi giải bất phương trình, thường cần xác định miền giá trị của biến để thỏa mãn điều kiện của bất phương trình.

1.2. Điều kiện để bất phương trình không có nghiệm

Một bất phương trình được coi là không có nghiệm (vô nghiệm) khi không có giá trị nào của biến thỏa mãn điều kiện của bất phương trình. Nói cách khác, không tồn tại giá trị hợp lệ nào cho biến sao cho biểu thức trong bất phương trình đạt yêu cầu đề ra.

Để giải bất phương trình, ta cần xác định các giá trị của biến thỏa mãn điều kiện và tìm phạm vi mà biểu thức có thể đạt được trong miền giá trị của biến. Nếu phạm vi này không giao với miền giá trị của biến, nghĩa là không có giá trị nào làm cho biểu thức thỏa mãn điều kiện, thì bất phương trình sẽ không có nghiệm.

Ví dụ: Xét bất phương trình x² + 1 < 0. Để giải bài toán này, ta cần tìm giá trị của biến x sao cho x² + 1 nhỏ hơn 0. Tuy nhiên, không có số nào có thể làm cho x² + 1 nhỏ hơn 0 vì bất kỳ số nào bình phương đều không nhỏ hơn 0 (vì bình phương của bất kỳ số nào cũng là số không âm). Do đó, không có giá trị nào của x thỏa mãn điều kiện và bất phương trình này vô nghiệm.

Một cách khác để hiểu điều kiện vô nghiệm là xem xét sự giao cắt giữa đồ thị của biểu thức và trục hoành. Nếu đồ thị không cắt trục hoành (tức là không có phần nào của đồ thị nằm dưới trục hoành), thì bất phương trình sẽ không có nghiệm.

1.3. Ý nghĩa tổng quát của bất phương trình

Bất phương trình là công cụ toán học quan trọng và có nhiều ứng dụng trong đời sống thực tiễn. Dưới đây là những điểm nổi bật về ý nghĩa của bất phương trình:

Xác định điều kiện tồn tại: Giải bất phương trình cho phép biết liệu có giá trị của biến nào thỏa mãn một điều kiện cụ thể không. Điều này đặc biệt quan trọng trong việc đánh giá khả năng thực hiện của các tình huống hoặc bài toán. Ví dụ, trong vật lý, xác định điều kiện để hệ thống vật lý duy trì sự cân bằng là ứng dụng của bất phương trình.

Giải quyết vấn đề thực tế: Bất phương trình được dùng để giải quyết các vấn đề thực tế như tối ưu hóa, xác định điều kiện tối đa hoặc tối thiểu, phân loại, và nhiều lĩnh vực khác trong khoa học, kinh tế, công nghệ, xã hội học, và quản lý. Ví dụ, trong kỹ thuật, bất phương trình giúp tối ưu hóa hiệu suất của các hệ thống kỹ thuật phức tạp.

Nghiên cứu mối quan hệ và biến động: Bất phương trình hỗ trợ nghiên cứu các mối quan hệ phức tạp giữa các biến và hiểu rõ cách các yếu tố ảnh hưởng lẫn nhau trong hệ thống. Trong nghiên cứu khoa học, bất phương trình thường dùng để kiểm tra và chứng minh các giả thuyết về mối liên hệ giữa các biến trong nghiên cứu.

2. Xác định giá trị m để bất phương trình không có nghiệm, kèm theo các bài tập và đáp án chi tiết

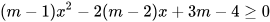
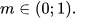
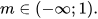
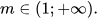
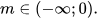
Giải thích:

Do hệ số của x² phụ thuộc vào m, ta cần xem xét hai trường hợp sau:

Trường hợp 1: Khi m - 1 = 0, suy ra m = 1. Thay m = 1 vào bất phương trình, ta thấy không đáp ứng được yêu cầu của bài toán.

Trường hợp 2: Ta có:

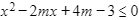
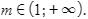
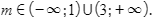
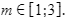
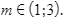
Giải pháp:

Bất phương trình không có nghiệm khi:

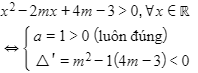
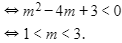
Lựa chọn D.

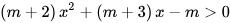
Giải thích:

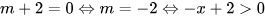
Vậy với m = -2, bất phương trình sẽ có nghiệm.

Để bất phương trình không có nghiệm, ta cần có điều kiện sau:

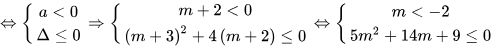
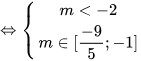
Do đó, không tồn tại giá trị nào của m để làm cho bất phương trình không có nghiệm.

3. Để giải quyết hiệu quả các bài tập về bất phương trình, học sinh cần thực hiện những bước nào?

Khó khăn trong việc giải toán bất phương trình là điều thường gặp đối với học sinh. Mức độ khó có thể khác nhau tùy thuộc vào độ phức tạp của bài toán và khả năng của bạn trong việc xử lý các dạng bất phương trình. Một số bài toán đơn giản có thể giải quyết dễ dàng, trong khi những bài toán phức tạp hơn có thể yêu cầu kiến thức sâu rộng và các phương pháp giải đặc biệt. Để học tốt bất phương trình, bạn có thể thực hiện các bước sau:

Nắm vững kiến thức nền: Trước khi bắt đầu với bất phương trình, hãy đảm bảo rằng bạn đã hiểu rõ các kiến thức cơ bản về biểu thức đại số, bất đẳng thức và cách giải các phương trình cơ bản. Những kiến thức này là nền tảng quan trọng để tiếp cận bất phương trình một cách hiệu quả.

Hiểu rõ các quy tắc và tính chất: Nắm vững các quy tắc cơ bản của bất phương trình, như cộng, trừ, nhân, chia các mũ, cách đưa các biểu thức về cùng một vế và điều kiện đảo ngược dấu trong bất phương trình,... là rất cần thiết. Các quy tắc và tính chất này là cơ sở để tìm ra hướng giải cho bất phương trình.

Thực hành nhiều bài tập mẫu: Hãy giải nhiều bài tập mẫu về bất phương trình để rèn luyện kỹ năng và làm quen với các dạng bài tập phổ biến. Nên bắt đầu với các bài tập cơ bản trước, và chọn những bài tập có đáp án để tự kiểm tra và củng cố kiến thức. Đừng vội làm các bài tập phức tạp.

Xem xét các ví dụ minh họa: Xem các ví dụ cụ thể trong sách giáo khoa hoặc tài liệu học tập. Hiểu cách giải các bài tập về bất phương trình từ những ví dụ trong sách giáo khoa, vì đây là nguồn kiến thức chuẩn xác nhất. Đặt câu hỏi và làm rõ những vấn đề còn nghi ngờ với thầy cô và bạn bè.

Học các phương pháp giải đặc thù: Nắm vững các phương pháp giải cho các loại bất phương trình đặc biệt như bất phương trình bậc nhất, bậc hai, có mũ, hoặc hệ bất phương trình,... Cần lưu ý rằng các phương pháp này có thể yêu cầu kiến thức chuyên biệt và quy trình giải riêng biệt.