Xác định tâm của đường tròn nội tiếp, ngoại tiếp tam giác và tứ giác

1. Đường tròn nội tiếp và ngoại tiếp là gì?

- Khái niệm:

+ Đường tròn đi qua tất cả các đỉnh của một đa giác gọi là đường tròn ngoại tiếp đa giác, còn đa giác này gọi là nội tiếp đường tròn.

+ Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp, và đa giác này được gọi là ngoại tiếp đường tròn.

- Định lý:

+ Mỗi đa giác đều có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

+ Tâm của đường tròn ngoại tiếp và đường tròn nội tiếp trùng nhau, được gọi là tâm của đa giác đều.

+ Tâm này là điểm giao nhau của hai đường trung trực của các cạnh hoặc hai đường phân giác của các góc.

- Công thức tính bán kính của đường tròn ngoại tiếp và nội tiếp trong đa giác đều.

Đối với đa giác đều n cạnh với mỗi cạnh dài a, R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp.

Ta có:

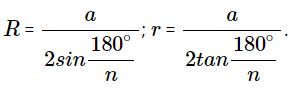
- Mở rộng:

+ Bán kính của đường tròn ngoại tiếp đa giác là khoảng cách từ tâm đến các đỉnh của đa giác.

+ Bán kính của đường tròn nội tiếp đa giác là khoảng cách từ tâm O đến một cạnh của đa giác.

+ Đối với đa giác đều có n cạnh, mỗi cạnh dài a.

Khi đó:

- Chu vi của đa giác là: 2p = na (trong đó p là nửa chu vi).

- Mỗi góc ở đỉnh của đa giác có số đo bằng

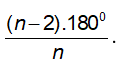
- Mỗi góc ở tâm của đa giác đều có số đo là 360° chia cho n.

Bán kính của đường tròn ngoại tiếp

Bán kính của đường tròn nội tiếp

Mối quan hệ giữa bán kính đường tròn ngoại tiếp và nội tiếp là:

R² - r² = a² / 4

Diện tích của đa giác đều

S = 1/2 . na . r

Ví dụ minh họa:

Cho một đường tròn có bán kính R = 3 cm.

Tính diện tích của hình vuông nội tiếp trong đường tròn này.

Giải pháp:

Chúng ta có: Bán kính của đường tròn ngoại tiếp là:

Vì tứ giác nội tiếp là một hình vuông với n = 4, do đó: a = R√2 = 3√2.

Diện tích của hình vuông được tính là: S = a² = (3√2)² = 18 cm².

2. Xác định tâm của đường tròn nội tiếp và đường tròn ngoại tiếp trong tam giác

- Khi ba cạnh của một tam giác là các tiếp tuyến của một đường tròn và đường tròn này nằm hoàn toàn bên trong tam giác, thì đường tròn đó được gọi là đường tròn nội tiếp tam giác.

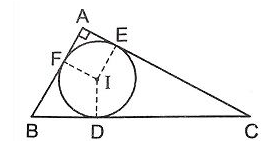
Đường tròn nội tiếp tam giác ABC với tâm I

– Đường tròn ngoại tiếp tam giác là đường tròn đi qua tất cả ba đỉnh của tam giác. Nói cách khác, tam giác này nằm hoàn toàn bên trong đường tròn.

Đường tròn ngoại tiếp tam giác ABC với tâm I

- Phương pháp xác định tâm của đường tròn nội tiếp và ngoại tiếp tam giác:

Để xác định tâm của đường tròn nội tiếp và ngoại tiếp trong tam giác, các bạn cần nhớ các lý thuyết sau:

+ Tâm của đường tròn nội tiếp tam giác là điểm giao của ba đường phân giác trong của tam giác (có thể là hai đường phân giác).

+ Tâm của đường tròn ngoại tiếp tam giác là điểm giao của ba đường trung trực của ba cạnh tam giác (hoặc có thể là điểm giao của hai đường trung trực).

- Tính toán các yếu tố liên quan đến đa giác nội tiếp và ngoại tiếp.

Phương pháp giải quyết:

Chúng ta áp dụng các khái niệm và công thức sau đây:

- Bán kính của đường tròn ngoại tiếp đa giác chính là khoảng cách từ tâm đường tròn đến một đỉnh bất kỳ của đa giác.

- Bán kính của đường tròn nội tiếp đa giác là khoảng cách từ tâm đường tròn đến một cạnh bất kỳ của đa giác.

- Với một đa giác đều n cạnh có mỗi cạnh dài a, ta có:

+ Chu vi của đa giác được tính bằng: c = n.a (với c là chu vi và a là độ dài của cạnh).

+ Mỗi góc tại đỉnh của đa giác có số đo là [(n − 2) × 180°] / n.

+ Mỗi góc tại tâm của đa giác có số đo là 360° / n.

+ Bán kính đường tròn ngoại tiếp được tính bằng: R = a / (2 × sin(180° / n))

⇒ a = 2 × R × sin(180° / n).

+ Bán kính đường tròn nội tiếp được tính bằng: r = a / (2 × tan(180° / n)) ⇒ a = 2 × r × tan(180° / n).

- Diện tích của đa giác đều được tính bằng công thức: S = 1/2 n . a . r (đơn vị diện tích).

- Bài tập ví dụ

Bài tập 1:

Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác ABC.

Biết rằng tam giác ABC là tam giác đều với mỗi cạnh dài 6cm.

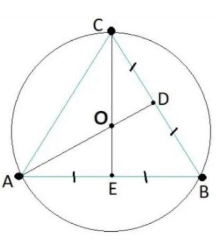
Hướng dẫn cách giải

Gọi D là trung điểm của cạnh BC và E là trung điểm của cạnh AB.

Đoạn thẳng AD cắt cạnh CE tại điểm O.

Trong tam giác đều ABC, đường trung tuyến cũng đồng thời là đường cao, đường phân giác và đường trung trực.

Điểm O là giao điểm của ba đường trung trực, vì vậy O chính là tâm của đường tròn ngoại tiếp tam giác.

Trong tam giác ABC, CE là đường trung tuyến

=> CE đồng thời là đường cao.

Áp dụng định lý Pytago cho tam giác vuông AEC, ta có:

CE^2 = AC^2 – AE^2 = 36 – 9 = 25, nên CE = 5.

Hơn nữa, điểm O là trọng tâm của tam giác ABC, do đó:

CO = 2/3 CE = 2/3 x 5 = 10/3.

Vậy, tâm của đường tròn ngoại tiếp tam giác ABC là O với bán kính:

OC = 10/3.

3. Xác định tâm của đường tròn nội tiếp và đường tròn ngoại tiếp tứ giác

Bài tập 1:

a) Vẽ một đường tròn với tâm tại O và bán kính 2cm.

b) Vẽ một hình vuông nội tiếp đường tròn (O) từ câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b), sau đó vẽ đường tròn (O; r).

Hướng dẫn giải

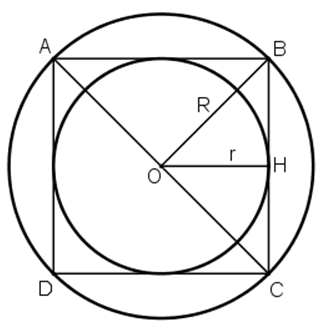
a) Đặt điểm O là tâm, dùng compa với bán kính 2cm để vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hai đường kính AC và BD cắt nhau vuông góc.

Nối các điểm A với B, B với C, C với D, và D với A để tạo thành tứ giác ABCD, một hình vuông nội tiếp đường tròn (O; 2cm).

c) Vẽ đường OH vuông góc với BC.

⇒ OH chính là khoảng cách từ tâm O đến đường thẳng BC.

Vì AB = BC = CD = DA (ABCD là hình vuông) nên khoảng cách từ tâm O đến các cạnh AB, BC, CD, DA đều bằng nhau (theo định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây).

⇒ O là tâm của đường tròn nội tiếp trong hình vuông ABCD.

OH là bán kính r của đường tròn nội tiếp trong hình vuông ABCD.

Trong tam giác vuông OBC, OH là đoạn trung tuyến:

=> OH = 1/2 BC = BH

Xem xét tam giác vuông OHB với các đặc điểm sau:

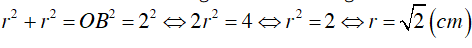
Vẽ một đường tròn với tâm O và bán kính OH. Đường tròn này sẽ nội tiếp hình vuông và tiếp xúc với bốn cạnh của hình vuông tại các điểm giữa của từng cạnh.

Bài 2:

Xem hình vuông dưới đây,

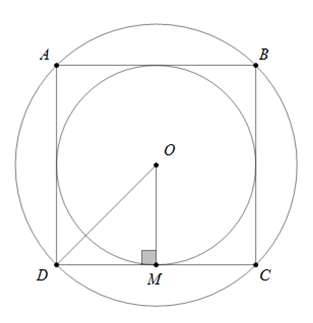
Nhận xét nào dưới đây là chính xác?

A. Bán kính của đường tròn ngoại tiếp hình vuông luôn lớn hơn bán kính của đường tròn nội tiếp hình vuông đó.

B. Bán kính của đường tròn ngoại tiếp bằng với bán kính của đường tròn nội tiếp trong hình vuông.

C. Bán kính của đường tròn ngoại tiếp luôn nhỏ hơn bán kính của đường tròn nội tiếp trong hình vuông.

D. Bán kính của đường tròn ngoại tiếp bằng một nửa bán kính của đường tròn nội tiếp trong hình vuông.

Đáp án là A

Hướng dẫn giải:

Xem xét hình vuông ABCD với tâm O, vẽ đường OM vuông góc với CD tại M.

Trong trường hợp này, OD là bán kính của đường tròn ngoại tiếp.

OM là bán kính của đường tròn nội tiếp trong hình vuông ABCD.

Tam giác ΔOMD vuông tại M nên OD ≥ OM (1).

Nếu OD = OM, thì đường tròn nội tiếp và đường tròn ngoại tiếp sẽ trùng nhau vì chúng có cùng tâm O và bán kính bằng nhau.

Khi đó, không thể có hình vuông nào vừa có đỉnh nằm trên đường tròn (O) vừa có cạnh tiếp xúc với đường tròn (O).

Do vậy, với OD ≠ OM, từ (1) ta suy ra OD > OM (đpcm).

Bài 3:

Xem xét lục giác đều ABCDEF với tâm O.

Gọi R và r lần lượt là bán kính của đường tròn ngoại tiếp và nội tiếp lục giác.

Viết công thức liên hệ giữa bán kính R và bán kính r.

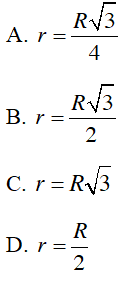
Hướng dẫn giải:

Đáp án là B

Vì lục giác đều ABCDEF chia đường tròn ngoại tiếp thành 6 cung có độ dài bằng nhau,

do đó:

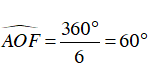
Tam giác AOF cân tại O có:

Vẽ đường cao AH trong ΔAOF.

Lúc này: OH = r, AH = R / 2.

Xem xét ΔAOH vuông tại H, do đó

Trân trọng!