Trên hành trình chinh phục toán học, 7 hằng đẳng thức lớp 8 luôn là công cụ quan trọng không thể thiếu. Khi nắm vững 7 hằng đẳng thức này, bạn không chỉ nhanh chóng giải quyết các bài toán mà còn áp dụng chúng trong nhiều tình huống thực tiễn. Bài viết này sẽ cung cấp cái nhìn tổng quan về các công thức, kèm theo ví dụ minh họa cụ thể để bạn dễ dàng áp dụng vào thực tế.
Khái niệm về hằng đẳng thức
Hằng đẳng thức là những công thức toán học đặc biệt, được diễn đạt dưới dạng phương trình thể hiện sự cân bằng tuyệt đối giữa hai biểu thức. Điều đặc biệt của các hằng đẳng thức là tính bất biến, luôn đúng với mọi giá trị của các biến số. Dù có thay đổi giá trị của các biến, hai vế của đẳng thức vẫn luôn bằng nhau.
7 hằng đẳng thức đáng nhớ trong chương trình lớp 8 là nền tảng quan trọng, giúp học sinh tiếp cận các bài toán đại số một cách logic và hiệu quả. Việc hiểu rõ những hằng đẳng thức này không chỉ hỗ trợ giải toán mà còn giúp phát triển khả năng tư duy phân tích, suy luận trong nhiều lĩnh vực khác nhau.

7 hằng đẳng thức cơ bản không thể quên
Dưới đây là 7 hằng đẳng thức lớp 8 quan trọng mà bạn cần nắm vững và áp dụng thành thạo:
Bình phương của một tổng
(a + b)² = a² + 2ab + b²
Hằng đẳng thức này khẳng định rằng bình phương của tổng hai số tự nhiên bất kỳ sẽ bằng tổng của bình phương số đầu, cộng với bình phương số thứ hai và thêm vào đó là hai lần tích của số đầu và số thứ hai.
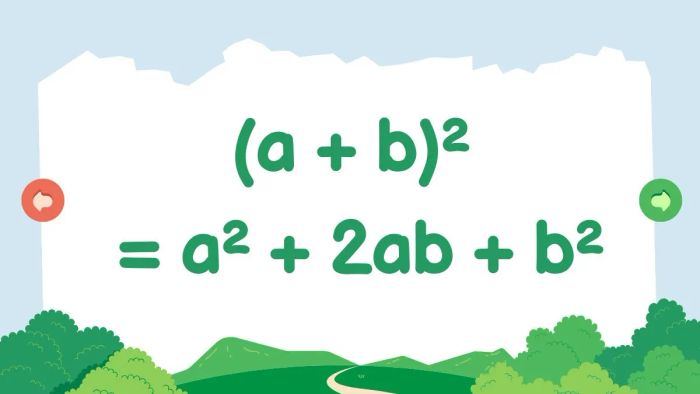
Ví dụ thực tế:
Một mảnh đất hình vuông có chiều dài mỗi cạnh là a mét. Người ta quyết định mở rộng mỗi cạnh thêm b mét.
- Diện tích của mảnh đất ban đầu là: a²
- Diện tích của mảnh đất sau khi được mở rộng là: (a + b)²
Như vậy, hằng đẳng thức này cho phép ta tính diện tích của mảnh đất mới: (a + b)² = a² + 2ab + b² (diện tích hình vuông ban đầu cộng với hai lần diện tích của hình chữ nhật a x b, cộng thêm diện tích của hình vuông nhỏ b²)
Bình phương của một hiệu
(a - b)² = a² - 2ab + b²
Khi ta lấy hiệu của hai số rồi bình phương kết quả, ta sẽ nhận được kết quả bằng bình phương số đầu tiên trừ đi hai lần tích của cả hai số, rồi cộng với bình phương của số thứ hai.
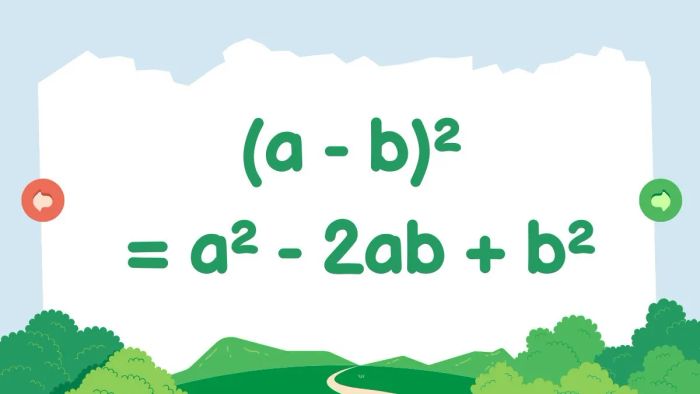
Ví dụ thực tế: Một tấm bìa hình vuông có cạnh dài a cm. Sau đó, người ta cắt một hình vuông nhỏ ở góc của tấm bìa, với cạnh là b cm
- Diện tích tấm bìa ban đầu là: a²
- Diện tích tấm bìa sau khi cắt bỏ phần hình vuông là: (a - b)²
Hằng đẳng thức này thể hiện diện tích tấm bìa sau khi cắt: (a - b)² = a² - 2ab + b² (diện tích hình vuông ban đầu trừ đi hai lần diện tích hình chữ nhật a x b, cộng với diện tích của hình vuông nhỏ b²)
Hiệu hai bình phương
a² - b² = (a + b)(a - b)
Hiệu của hai số bình phương bằng tổng của số đầu và số thứ hai nhân với hiệu của số đầu và số thứ hai.
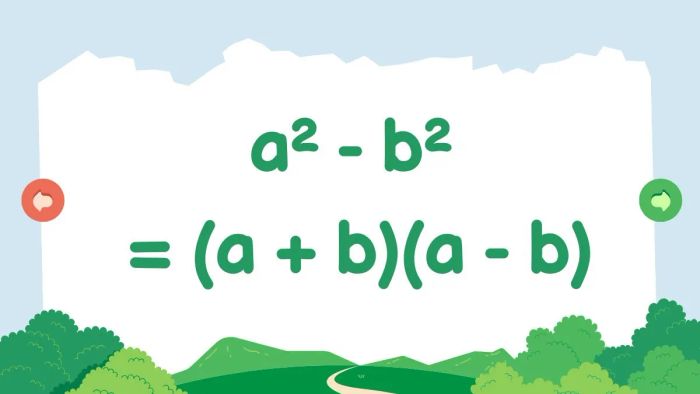
Ví dụ thực tế: Một hình chữ nhật có chiều dài a mét, chiều rộng b mét. Ta cắt dọc theo chiều rộng một đoạn b mét và ghép nó vào chiều dài.
- Diện tích hình chữ nhật ban đầu là: ab
- Hình mới tạo thành có chiều dài (a + b), chiều rộng (a - b) và diện tích là: (a + b)(a - b)
- Vì diện tích không đổi nên ta có: a² - b² = (a + b)(a - b)
Lập phương của một tổng
(a + b)³ = a³ + 3a²b + 3ab² + b³
Với mọi giá trị thực của a và b, ta có công thức: lập phương của tổng hai số bằng tổng của lập phương số đầu tiên, ba lần tích bình phương của số đầu tiên với số thứ hai, ba lần tích của số đầu tiên với bình phương của số thứ hai, và cuối cùng là lập phương của số thứ hai.
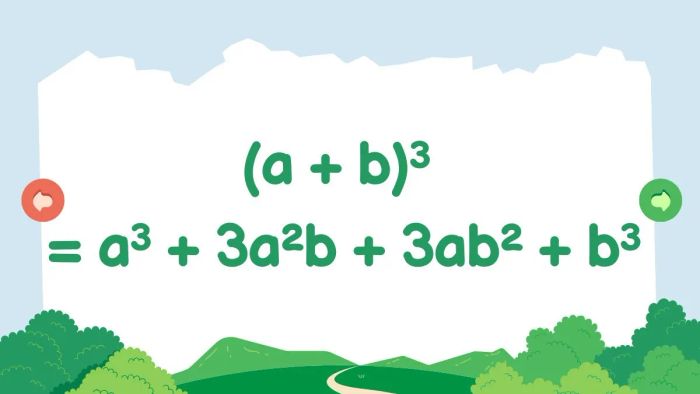
Ví dụ thực tế: Hãy tưởng tượng một khối lập phương lớn có cạnh là (a + b). Khối lập phương này được cấu thành từ 8 khối nhỏ: một khối lập phương có cạnh a, một khối lập phương có cạnh b, ba khối hộp chữ nhật có kích thước a x a x b và ba khối hộp chữ nhật có kích thước a x b x b.
- Thể tích của khối lập phương lớn là: (a + b)³
- Tổng thể tích của các khối nhỏ là: a³ + 3a²b + 3ab² + b³
Lập phương của một hiệu
(a - b)³ = a³ - 3a²b + 3ab² - b³
Với bất kỳ giá trị thực nào của a và b, ta có công thức: lập phương của hiệu hai số bằng lập phương của số đầu tiên trừ đi ba lần tích của bình phương số đầu tiên với số thứ hai, cộng với ba lần tích của số đầu tiên với bình phương của số thứ hai và cuối cùng trừ đi lập phương của số thứ hai.
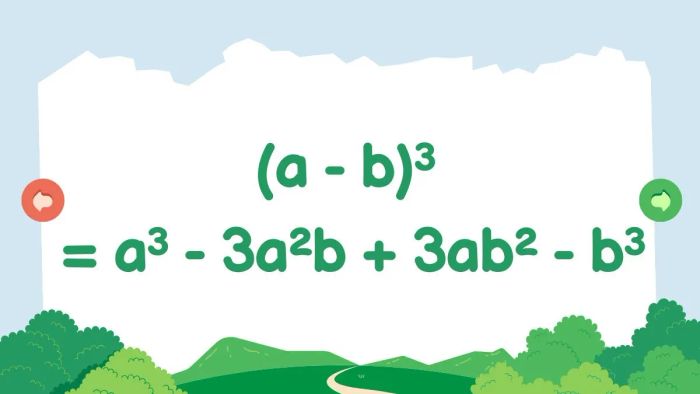
Ví dụ thực tế: Tương tự như trên, lần này ta xét một khối lập phương lớn có cạnh a, sau đó khoét đi một khối lập phương nhỏ có cạnh b cùng với các khối hộp chữ nhật tương ứng.
- Thể tích còn lại của khối lập phương lớn là: (a - b)³
- Thể tích này chính là thể tích của khối lập phương cạnh a trừ đi thể tích của khối lập phương cạnh b và các khối hộp chữ nhật tương ứng.
Tổng hai lập phương
a³ + b³ = (a + b)(a² - ab + b²)
Tổng lập phương của hai số thực bất kỳ có thể được biểu diễn như một tích của tổng hai số này với ba hạng tử: bình phương của số đầu tiên, trừ đi tích của hai số và cộng thêm bình phương của số thứ hai.
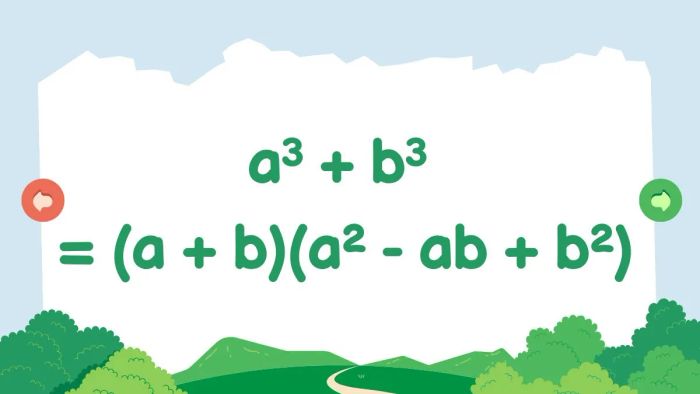
Chẳng hạn:
p³ + 8 = p³ + 2³ = (p + 2)(p² - 2p + 4)
Biểu thức p² - 2p + 4 là "bình phương thiếu của hiệu giữa p và 2".
Việc nắm vững 7 hằng đẳng thức lớp 8 đóng vai trò quan trọng giúp con bạn vững bước trên con đường học toán. Để học hiệu quả hơn, hãy trang bị cho con chiếc điện thoại thông minh với ứng dụng học tập trực tuyến. Cửa hàng trực tuyến Mytour luôn có các ưu đãi hấp dẫn để hỗ trợ quá trình học của học sinh. Hãy truy cập vào liên kết dưới đây để tìm hiểu thêm bạn nhé.
Hiệu của hai lập phương
a³ - b³ = (a - b)(a² + ab + b²)
Với hai số thực bất kỳ, khi lấy lập phương của số thứ nhất trừ đi lập phương của số thứ hai, kết quả sẽ là tích của hiệu giữa hai số và tổng của bình phương số đầu tiên, tích của hai số và bình phương số thứ hai.
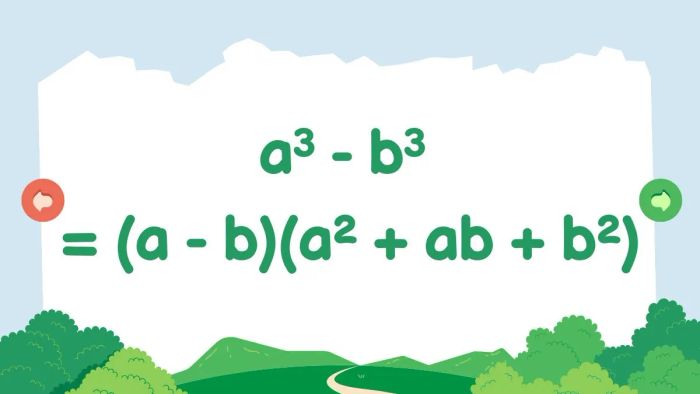
Chẳng hạn:
q³ - 27 = q³ - 3³ = (q - 3)(q² + 3q + 9)
Lưu ý, q² + 3q + 9 chính là bình phương thiếu của tổng giữa q và 3, chỉ thiếu đi phần (-2ab) so với hằng đẳng thức bình phương của một tổng.
Ứng dụng của hằng đẳng thức trong giải toán
7 hằng đẳng thức quan trọng được nêu ra có nhiều ứng dụng thiết thực trong việc giải toán, giúp đơn giản hóa các phép tính phức tạp và hỗ trợ giải quyết những bài toán khó. Sau đây là một số ứng dụng phổ biến trong toán học.
Rút gọn biểu thức
7 hằng đẳng thức lớp 8 quan trọng giúp rút gọn những biểu thức đại số phức tạp, biến chúng trở nên dễ dàng và tiện lợi hơn trong quá trình giải quyết.
Chẳng hạn: Tối giản biểu thức (x + 2)² - (x - 2)²
Chọn áp dụng hằng đẳng thức "bình phương của một tổng" và "bình phương của một hiệu" để thực hiện, ta có:
(x + 2)² - (x - 2)² = (x² + 4x + 4) - (x² - 4x + 4) = 8x
Nhận diện và tính giá trị biểu thức nhanh chóng
Thông qua việc nhận dạng các mẫu hằng đẳng thức, ta có thể tính toán giá trị của các biểu thức một cách nhanh gọn mà không cần thực hiện các phép toán phức tạp.

Chẳng hạn: Tính nhanh 102²
Có thể viết lại 102² = (100 + 2)²
Áp dụng hằng đẳng thức "bình phương của một tổng", ta có:
(100 + 2)² = 100² + 2.100.2 + 2² = 10000 + 400 + 4 = 10404
Giải phương trình và bất phương trình
7 hằng đẳng thức quan trọng trong chương trình lớp 8 được ứng dụng để giải các phương trình và bất phương trình, đặc biệt là phương trình bậc hai và bậc ba.
Ví dụ: Giải phương trình x² - 9 = 0
Áp dụng hằng đẳng thức "hiệu của hai bình phương", ta có:
x² - 9 = x² - 3² = (x + 3)(x - 3) = 0
=> x + 3 = 0 hoặc x - 3 = 0
Do đó, x = -3 hoặc x = 3
Việc hiểu sâu và áp dụng thành thạo 7 hằng đẳng thức lớp 8 là yếu tố quan trọng giúp bạn giải quyết nhiều dạng bài toán một cách hiệu quả. Hãy luyện tập thường xuyên và áp dụng các hằng đẳng thức vào các bài tập cụ thể để nâng cao khả năng giải toán của bản thân. Đừng quên ghé thăm Mytour để khám phá thêm nhiều kiến thức toán học hữu ích.
