Các công thức tính thể tích trong các lĩnh vực như toán học, vật lý và hóa học

Bạn đã từng học các công thức tính thể tích nhưng giờ lại không nhớ rõ? Đây là khái niệm quan trọng, ứng dụng rộng rãi trong các ngành như vật lý, toán học và hóa học. Hãy cùng Mytour điểm qua các công thức tính thể tích của hình lập phương, lăng trụ, cầu,... một cách nhanh chóng và chính xác.

Thể tích là gì?

Thể tích là đại lượng đo lường không gian mà một vật thể chiếm giữ. Đây là phép đo ba chiều của vật thể, bao gồm chiều dài, chiều rộng và chiều cao. Đơn vị quốc tế (SI) dùng để đo thể tích là mét khối (m³) và lít (l) cho chất lỏng.

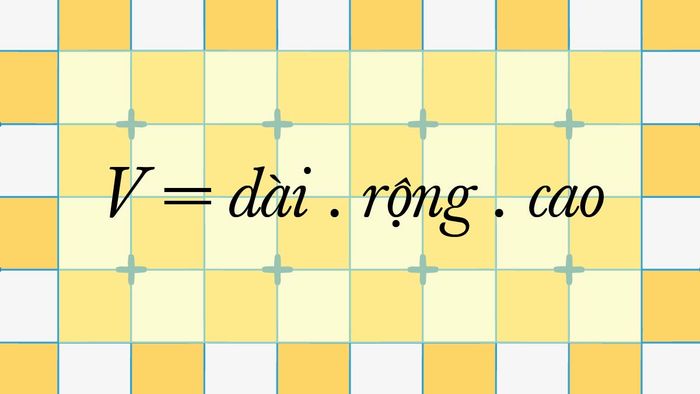
Dưới đây là bảng tổng hợp giúp bạn dễ dàng nắm bắt mối quan hệ giữa các đơn vị đo thể tích:

Kiến thức về thể tích rất phong phú và xuất hiện trong nhiều môn học khác nhau. Để việc học và nghiên cứu công thức trở nên dễ dàng hơn, hãy lựa chọn một chiếc laptop phù hợp. Ghé ngay Mytour để khám phá các thương hiệu laptop uy tín với giá cả hợp lý.

Những công thức phổ biến dùng để tính thể tích

Có vô vàn công thức thể tích từ các môn toán học, vật lý, hóa học, mỗi hình dạng đều có một cách tính riêng biệt. Làm sao để xác nhận bạn đã áp dụng đúng công thức? Hãy cùng tìm hiểu các công thức phân loại theo từng lĩnh vực tương ứng nhé.

Công thức tính thể tích trong toán học

Trong toán học, các công thức tính thể tích chủ yếu liên quan đến các hình khối đặc biệt như hộp chữ nhật và các hình khối khác.

• Công thức tính thể tích hình lập phương đơn giản và dễ áp dụng:

Hình lập phương là một khối đặc biệt trong không gian, với 6 mặt vuông có kích thước bằng nhau. Để tính thể tích của hình lập phương, bạn có thể sử dụng công thức sau:

V = a3

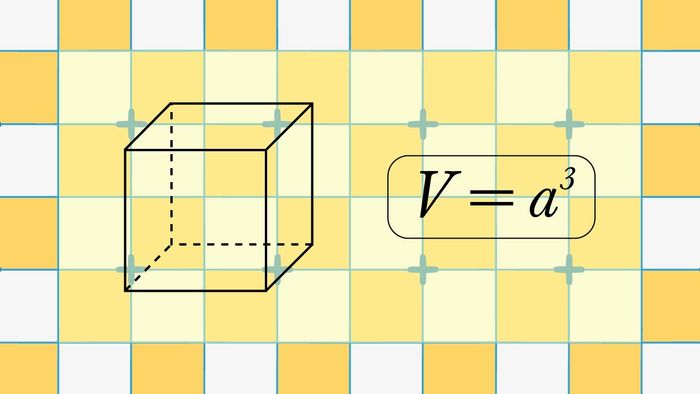
Trong đó, a đại diện cho chiều dài của cạnh.

• Công thức phổ biến để tính thể tích hình hộp chữ nhật:

Hình hộp chữ nhật là một khối ba chiều có 6 mặt phẳng, 8 đỉnh và 12 cạnh thẳng. Để tính thể tích của nó, bạn sử dụng công thức sau:

V = a.b.h

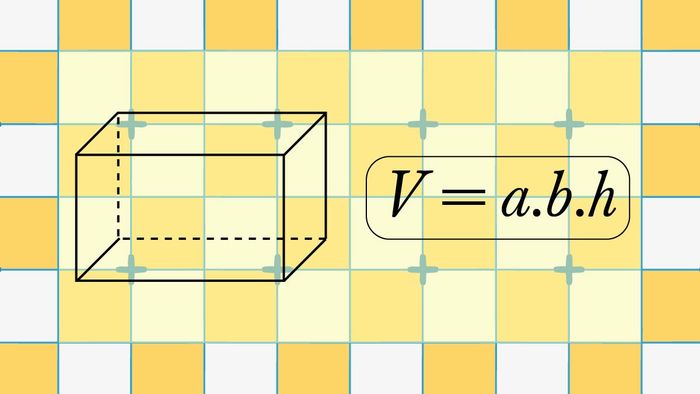
Công thức này được xây dựng dựa trên các yếu tố sau:

• V: thể tích của hình lập phương.
• a: độ dài của một cạnh của hình lập phương.
• b: không cần thiết vì tất cả các cạnh đều có chiều dài giống nhau.
• h: không cần thiết vì đây là hình khối đều với các cạnh đồng đều.

• Công thức chính xác để tính thể tích hình lập phương:

Hình lập phương là một khối hình học với tất cả các mặt đều là các hình vuông và mọi cạnh đều có chiều dài bằng nhau.

V = Sđáy.h

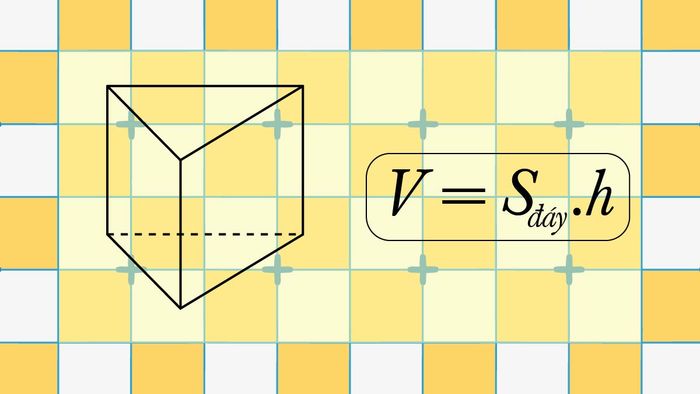
Công thức này được định nghĩa thông qua các yếu tố sau:

• Sđáy: diện tích của mặt đáy hình lăng trụ.
• h: chiều cao của lăng trụ, là khoảng cách từ đáy này đến đáy kia.

• Công thức tính thể tích hình cầu chính xác và nhanh chóng để giải bài toán hiệu quả:

Hình cầu là một khối 3D hoàn hảo, với mỗi điểm trên bề mặt có khoảng cách đều từ tâm. Nó được tạo ra khi một hình tròn xoay quanh đường kính của nó. Công thức tính thể tích của hình cầu phức tạp hơn các hình khác.

V = 4/3.π.r2

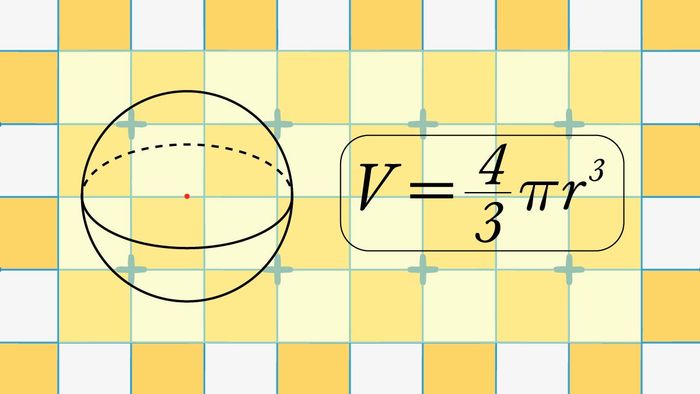
Công thức tính thể tích hình chữ nhật được xây dựng từ các yếu tố sau:

• π: hằng số Pi, với giá trị xấp xỉ là 3.14.
• r: bán kính của hình cầu.

Công thức tính thể tích trong lĩnh vực vật lý

Trong vật lý, thể tích của một vật có mối quan hệ tỉ lệ thuận với khối lượng của nó. Công thức tính thể tích như sau:

V = m/D

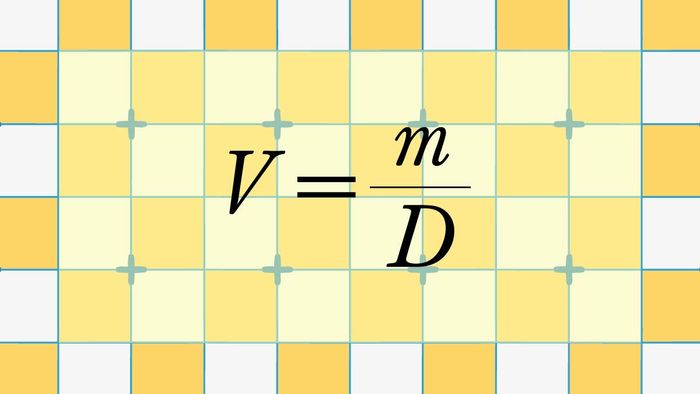
Công thức này bao gồm các yếu tố sau:

• m: khối lượng của vật (đơn vị: kg, g).
• D: khối lượng riêng của vật liệu cấu thành (đơn vị: kg/m³).

Để áp dụng công thức một cách hiệu quả, bạn cần nắm vững cách chuyển đổi giữa các đơn vị đo lường.

Công thức tính thể tích trong hóa học

Thể tích là yếu tố quan trọng trong các bài tập hóa học. Nó cũng đóng vai trò thiết yếu trong việc pha chế dung dịch. Một số công thức thể tích cơ bản trong hóa học bao gồm:

• Thể tích của khí:

• Trong điều kiện chuẩn, ký hiệu: ĐKTC.

V = n x 22.4

Công thức tính thể tích khí được xác định như sau:

• V: thể tích khí (đơn vị: lít).
• n: số mol khí (đơn vị: mol).
• 22.4: thể tích mol khí ở điều kiện chuẩn (đơn vị: lít/mol).

• Trong các điều kiện khác:

Phương trình lý tưởng cho khí lý tưởng: PV = nRT

Công thức này được xây dựng từ các yếu tố sau:

• P: áp suất của khí (đơn vị: atm).
• V: thể tích khí (đơn vị: lít).
• n: số mol khí (đơn vị: mol).
• R: hằng số khí lý tưởng, đơn vị: 0.821 L.atm/mol.K.
• T: nhiệt độ tuyệt đối (đơn vị: K).

• Dung tích trong dung dịch hóa học:

V = n/CM

Công thức này được xác định qua các yếu tố sau:

• n: số mol của chất tan (đơn vị: mol).
• CM: nồng độ mol của dung dịch (đơn vị: mol/l).

Ngoài ra, có một công thức tính thể tích không khí: Vkk = 5VO2.

Công thức chi tiết tính thể tích nước

Việc nắm vững và áp dụng các công thức tính mét khối nước là rất quan trọng, giúp chúng ta kiểm soát và sử dụng nguồn nước một cách hiệu quả trong cuộc sống hàng ngày và các lĩnh vực khác. Dưới đây là các công thức tính mét khối nước cho các hình dạng khác nhau như lập phương, cầu, trụ, ...:

Công thức tổng quát tính thể tích nước

Công thức tính thể tích nước phụ thuộc vào hình dạng của vật chứa nước. Đối với các hình dạng phổ biến, chúng ta sẽ sử dụng công thức chung để tính dung tích nước như sau:

V = a.b.h

Công thức này bao gồm các yếu tố sau:

• a,b: chiều dài và chiều rộng của bồn chứa nước.
• h: chiều sâu của bồn chứa nước.
• Các đơn vị đo thường sử dụng bao gồm lít (l), mét khối (m3), mililit (ml), hoặc các đơn vị tương tự.

Công thức tính thể tích nước trong bồn chứa

Thông thường, bồn chứa nước có dạng hình trụ, vì vậy chúng ta sẽ áp dụng công thức thể tích hình trụ để tính dung tích của bồn.

V = π.r2.h

Công thức này có các thành phần như sau:

• π: hằng số Pi, với giá trị xấp xỉ là 3.14.
• r: bán kính của đáy bồn chứa nước.
• h: chiều cao của bồn chứa nước.

Việc tính toán thể tích bồn chứa giúp xác định được khối lượng nước tối đa có thể chứa, tránh tình trạng thiếu hoặc thừa nước, từ đó đáp ứng đúng nhu cầu sử dụng.

Công thức tính thể tích cho bồn chứa hình vuông và hình chữ nhật

Bồn chứa nước hình chữ nhật và hình vuông là hai dạng phổ biến. Với các bồn có hình chữ nhật, ta sử dụng công thức tính thể tích hình chữ nhật như dưới đây:

V = a.b.h

Các yếu tố trong công thức:

• a: chiều dài của bồn chứa nước.
• b: chiều rộng của bồn nước.
• h: chiều sâu của bồn chứa nước.

Vì hình vuông là một trường hợp đặc biệt của hình chữ nhật với các cạnh có độ dài bằng nhau, ta có thể áp dụng công thức tính thể tích sau: V = a2.h

Công thức tính thể tích cho bồn hình tròn và hình lăng trụ

Bồn chứa nước hình tròn là lựa chọn phổ biến cho bể bơi. Trong không gian hình học, đây thực chất là một hình trụ, và thể tích của bồn sẽ được tính theo công thức dưới đây:

V = π.r2.h

Các tham số trong công thức là:

• π: hằng số Pi (π ≈ 3.14).
• r: bán kính đáy bồn. Nếu chỉ biết đường kính (d) của bồn, ta tính bán kính bằng cách chia d cho 2.
• h: chiều cao của bồn chứa nước.

Ngoài ra, thể tích của bồn hình lăng trụ có thể được tính bằng công thức sau:

V = Sđáy.h

Trong công thức trên:

• Sđáy: là diện tích của đáy bồn nước.
• h: là độ sâu của bồn nước.

Diện tích đáy của bồn hình lăng trụ có thể được tính theo các công thức khác nhau, tùy thuộc vào hình dạng của đáy.

• Đáy vuông: Sđáy = cạnh . cạnh.
• Đáy chữ nhật: Sđáy = chiều dài . chiều rộng.
• Đáy tam giác: Sđáy = (đáy . chiều cao) / 2. Trong đó, chiều cao tính theo công thức: cạnh .√3/2.

Công thức tính thể tích nước cho các hình dạng không rõ ràng

Khi không xác định được hình dạng cụ thể của bồn, việc tính toán sẽ khó khăn hơn, nhưng bạn vẫn có thể tham khảo hai phương pháp sau:

• Phương pháp 1: Chia vật thể thành các phần có hình dạng đơn giản. Tiến hành đo đạc kích thước từng phần và áp dụng công thức tương ứng. Cuối cùng, cộng lại thể tích của từng phần để có tổng thể tích.
• Phương pháp 2: Đo chiều dài, rộng và độ sâu tại nhiều vị trí khác nhau của vật thể. Tính giá trị trung bình của các kích thước rồi áp dụng công thức tính thể tích hình chữ nhật để tính tổng dung tích nước.

Công thức cơ bản để tính lưu lượng dòng chảy của nước

Bên cạnh các công thức tính thể tích, việc tính toán lưu lượng dòng chảy của nước cũng rất quan trọng trong thực tế. Lưu lượng nước thường được đo bằng các đơn vị: lít/giây (l/s) hoặc mét khối/giờ (m³/h).

Để tính lưu lượng, sử dụng công thức dưới đây:

Q = A.v

Giải thích các ký hiệu trong công thức:

Q: lưu lượng dòng chảy, có thể đo bằng m3/h hoặc l/s.

A: diện tích mặt cắt vuông góc với dòng chảy (m2), tính theo công thức: A = S = π.r2.

v: tốc độ trung bình của dòng nước (m/s). Công thức tính vận tốc là: v = √(2gh), với g là gia tốc trọng trường (≈ 9.8 m/s2) và h là chiều cao cột nước (m).

Bài tập về việc tính thể tích

Áp dụng các công thức trên vào các bài tập sẽ giúp bạn ghi nhớ lâu hơn và hiểu sâu hơn về lý thuyết. Biết đâu bạn sẽ gặp phải những bài tập này trong các kỳ thi sắp tới, phải không?

Bài tập tính thể tích trong môn Toán

Để giải quyết các bài toán này, bạn cần nắm vững công thức tính thể tích của các hình cầu, trụ, lập phương, hình chữ nhật, v.v.

Ví dụ 1:

Một hồ cá hình hộp chữ nhật có chiều dài 70cm, chiều rộng 40cm, chiều cao 30cm. Tính thể tích của bể cá này.

Cách giải:

Áp dụng công thức tính thể tích hình hộp chữ nhật, ta có: V = a.b.h = 70.40.30 = 84000 cm3 = 84 lít.

⇒ Thể tích của bể cá là 84000 cm3, tương đương 84 lít.

Ví dụ 2:

Cho hình trụ đứng tam giác đều (T) với tất cả các cạnh dài 4cm. Tính thể tích của (T).

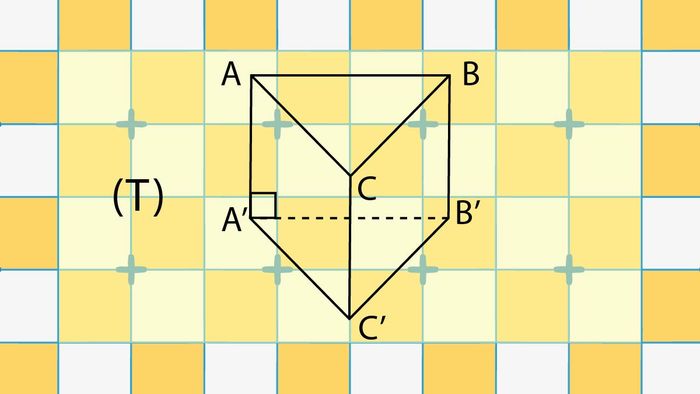
Giải thích:

Áp dụng công thức: V = Sđáy.h = SABC . AA’ = [½ . 2 . (2√3/2)] . 2 = 4√3/4 . 2 = 2√3 cm³.

Bài tập về thể tích trong vật lý

Các bài toán vật lý thường yêu cầu sử dụng công thức thể tích để tính toán khối lượng riêng của vật. Hãy giải bài tập dưới đây:

Tính thể tích 3 tấn cát, biết 8 lít cát có khối lượng 12kg.

Giải thích:

Chuyển đổi đơn vị: 1 lít = 1 dm³ = 1/1000 m³ ⇒ Mỗi 1/100 m³ cát có trọng lượng 12kg.

Khối lượng riêng của cát là: D = m/V = 12 / (1/100) = 1200 kg/m³.

Vậy 3 tấn = 3000 kg

Vậy thể tích của 3 tấn cát là: V = m/D = 1000/1200 = ⅚ m³.

Hãy áp dụng phương pháp này để giải quyết các bài tập tương tự mà bạn đã học trong lớp.

Bài tập tính thể tích trong môn Hóa học

Vì có nhiều công thức tính thể tích khác nhau, bạn cần xác định loại bài tập và lựa chọn công thức phù hợp. Đặc biệt, việc xác định số mol là rất quan trọng, vì nó là 'chìa khóa' để giải bài tập.

Ví dụ minh họa:

Phương trình phản ứng: CaCO3 → CaO + CO2. Nhiệt phân 100g CaCO3. Tính thể tích CO2 (ở điều kiện tiêu chuẩn).

Giải quyết bài toán:

Số mol CaCO3: nCaCO3 = mCaCO3 / MCaCO3 = 100/100 = 1 mol.

Dựa vào phương trình phản ứng, ta có: nCO2 = nCaCO3 = 1.

VCO2 = nCO2 . 22.4 = 1 . 22.4 = 22.4 lít.

Vậy là Mytour đã giúp bạn hiểu rõ các công thức tính thể tích trong toán học, vật lý và hóa học. Bài viết cũng cung cấp thêm phương pháp tính dung tích nước và các bài tập liên quan. Hy vọng bài viết này sẽ là tài liệu tham khảo hữu ích cho bạn. Nếu bạn có thêm câu hỏi, đừng ngần ngại để lại bình luận dưới bài viết nhé.