Việc nhận diện các trường hợp đồng dạng của tam giác là một yếu tố cốt lõi trong hình học, giúp học sinh phân biệt sự tương đồng giữa các tam giác dựa trên các tiêu chí góc và cạnh. Nắm vững lý thuyết này sẽ hỗ trợ học sinh giải quyết các bài toán thực tế, từ đó phát triển tư duy logic và khả năng phân tích hình học. Bài viết này sẽ giải thích chi tiết về các trường hợp đồng dạng, cùng với các bài tập ứng dụng để bạn hiểu rõ và ghi nhớ kiến thức.
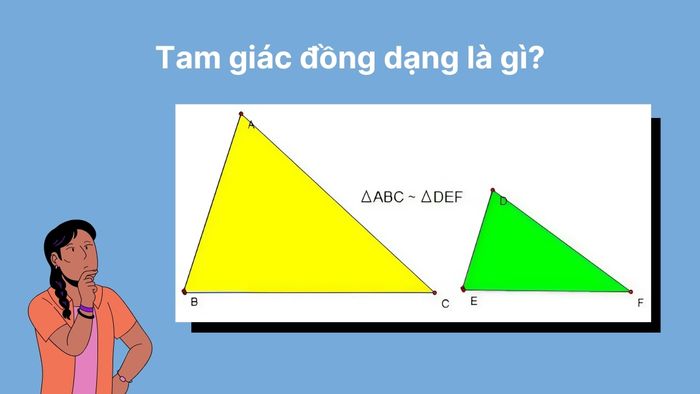
Khái niệm về tam giác đồng dạng
Khi ba góc của hai tam giác tương ứng bằng nhau và tỷ lệ các cạnh của chúng là giống nhau, hai tam giác này sẽ là đồng dạng. Điều này có nghĩa là dù kích thước của hai tam giác có thể khác nhau, nhưng hình dạng của chúng sẽ hoàn toàn giống nhau. Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại, nó sẽ tạo thành một tam giác mới, có tỷ lệ cạnh tương đương với tam giác ban đầu.
Các trường hợp đồng dạng của tam giác
Trong hình học, đồng dạng là một tính chất quan trọng giúp nhận diện những tam giác có hình dạng tương tự nhau, mặc dù kích thước có thể khác biệt. Việc nắm rõ ba trường hợp đồng dạng của tam giác không chỉ giúp giải quyết các bài toán mà còn có thể ứng dụng lý thuyết vào thực tế hiệu quả hơn.
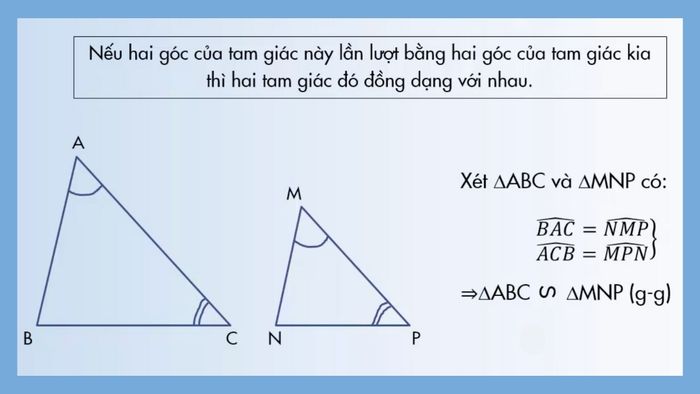
Trường hợp đồng dạng thứ nhất: Góc – Góc
Hai tam giác được xem là đồng dạng theo tiêu chí Góc – Góc khi chúng có hai cặp góc tương ứng bằng nhau. Điều này chỉ ra rằng các cạnh tương ứng của hai tam giác có tỷ lệ chiều dài đồng nhất. Ví dụ, trong tam giác ABC, góc BAC bằng góc NMP và góc ACB bằng góc MPN trong tam giác MNP, do đó hai tam giác này đồng dạng theo quy tắc Góc – Góc.
Laptop là công cụ tuyệt vời giúp học sinh nâng cao hiệu quả học tập môn Toán 8, đặc biệt là khi nghiên cứu các trường hợp đồng dạng của tam giác. Với khả năng kết nối internet nhanh chóng, dung lượng lưu trữ lớn, và độ bền cao, những chiếc laptop hiện đại trở thành người bạn đồng hành không thể thiếu trong việc truy cập tài liệu và tham gia các lớp học trực tuyến. Bạn có thể dễ dàng tìm thấy những chiếc laptop này tại Mytour để cải thiện việc học tập của mình.
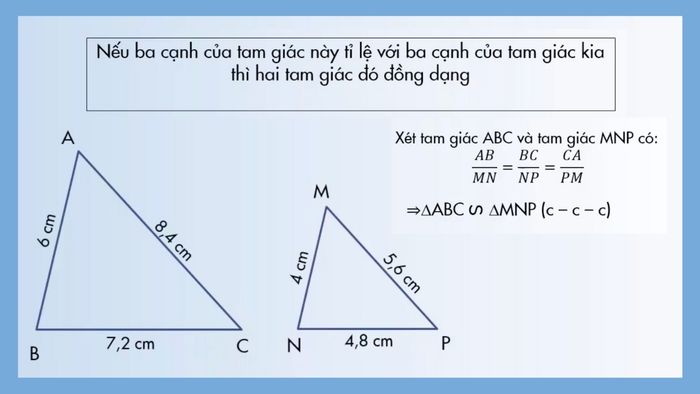
Trường hợp đồng dạng thứ hai: Cạnh – Cạnh – Cạnh
Hai tam giác ABC và MNP được xác định là đồng dạng theo quy tắc Cạnh – Cạnh – Cạnh khi tỷ lệ giữa ba cặp cạnh tương ứng của chúng là như nhau. Cụ thể, nếu AB/NM = BC/NP = CA/PM và các tỷ số này bằng nhau, thì hai tam giác này là đồng dạng. Ví dụ, nếu AB/NM = 6/4, BC/NP = 7,2/4,8, CA/PM = 8,4/5,6 thì tam giác ABC đồng dạng với tam giác MNP.
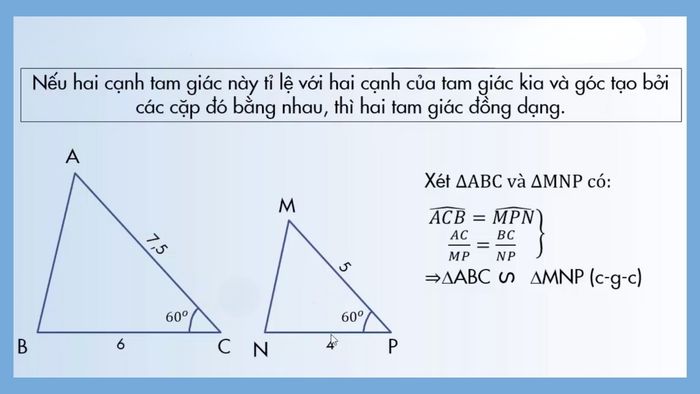
Trường hợp đồng dạng thứ ba: Cạnh – Góc – Cạnh
Hai tam giác được coi là đồng dạng khi tỷ lệ giữa hai cạnh tương ứng của chúng là giống nhau và góc giữa hai cạnh đó cũng bằng nhau. Ví dụ, tam giác ABC và tam giác MNP sẽ đồng dạng nếu góc ACB bằng góc MPN và AC/MP = BC/NP. Điều này được chứng minh qua trường hợp đồng dạng Cạnh – Góc – Cạnh.
Cách chứng minh hai tam giác đồng dạng
Để xác định hai tam giác có đồng dạng hay không, bạn có thể sử dụng các phương pháp hình học phù hợp dựa trên thông tin bài toán cung cấp.
- Cách 1: Một phương pháp để chứng minh hai tam giác đồng dạng là sử dụng một trong ba tiêu chí để xác định tính đồng dạng của chúng.
- Cách 2: Áp dụng định lý Talet, khi một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại tại các điểm khác nhau, sẽ tạo ra các đoạn thẳng có tỷ lệ tương ứng giữa chúng.
- Cách 3: Xác định các điều kiện cần và đủ để chứng minh hai tam giác đồng dạng. Sự đồng dạng xảy ra khi các cạnh của tam giác có tỷ lệ giống nhau. Nếu hai góc của một tam giác bằng hai góc của tam giác còn lại, thì chúng cũng đồng dạng. Thêm vào đó, nếu hai góc nằm giữa các cạnh tương ứng có độ lớn giống nhau, thì hai tam giác cũng sẽ đồng dạng.

Bài tập về các trường hợp đồng dạng của tam giác
- Xem xét tam giác ABC với chiều dài các cạnh lần lượt là AB = 5cm, BC = 9cm và CA = 8cm. Tam giác MNP có các cạnh MN = 4cm, NP = 7.2cm, PM = 6.4cm. Hãy chứng minh liệu hai tam giác này có đồng dạng hay không.
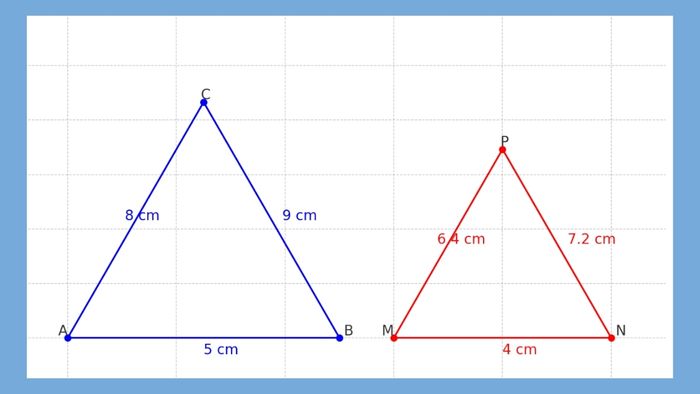
Lời giải: Hai tam giác này đồng dạng theo trường hợp Cạnh - Cạnh - Cạnh (CCC) vì các cặp cạnh tương ứng có tỷ lệ giống nhau: AB/MN = BC/NP = CA/PM = 1,25 cm.
- Cho tam giác MNP với MN nhỏ hơn MP, MI là đường phân giác trong. Vẽ tia Px ngoài tam giác sao cho góc NPx bằng góc NMI. Điểm K là giao điểm của MI và Px. Hãy chứng minh tam giác MIN đồng dạng với tam giác PIK.
Lời giải:
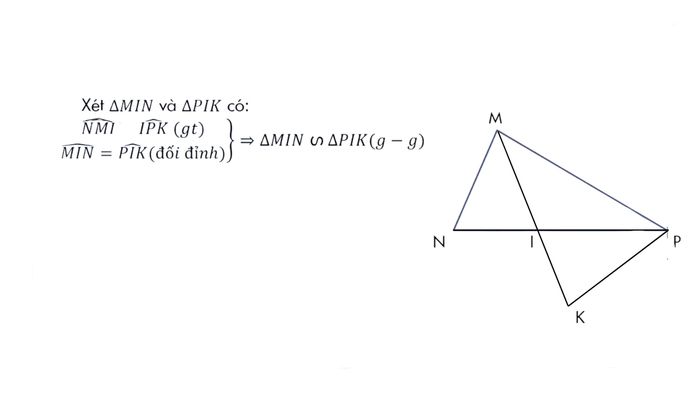
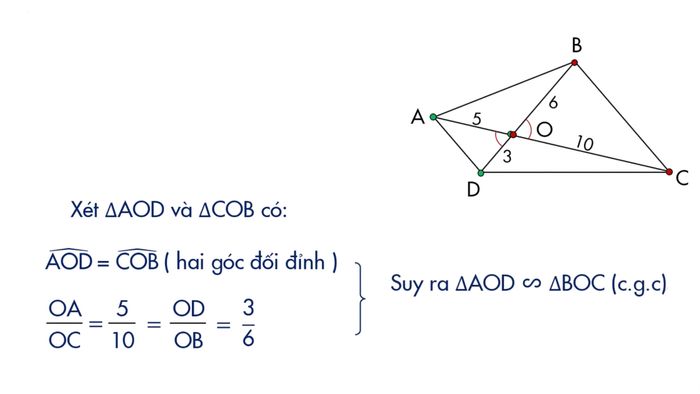
Liệu tam giác AOD và tam giác COB có đồng dạng hay không trong hình vẽ dưới đây?
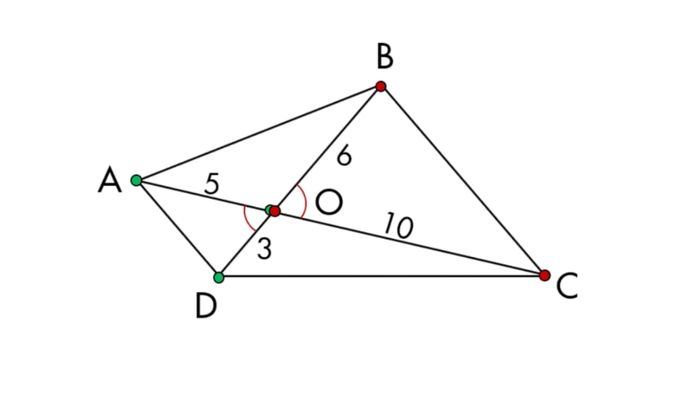
Lời giải:
Hiểu rõ các trường hợp đồng dạng của tam giác không chỉ giúp bạn giải quyết bài toán một cách nhanh chóng mà còn rèn luyện khả năng tư duy hình học sắc bén. Việc áp dụng linh hoạt các nguyên lý về đồng dạng sẽ giúp bạn nắm vững các mối liên hệ và đặc điểm của các hình học trong không gian. Hy vọng rằng bài viết này đã cung cấp những kiến thức hữu ích để bạn tự tin làm bài tập và ứng dụng vào thực tiễn.
