Gặp khó khăn trong việc tính nguyên hàm bằng tay? Bài viết này sẽ chỉ bạn cách bấm nguyên hàm trên máy Casio 580 chi tiết, giúp bạn dễ dàng giải quyết các bài toán.
Kiến thức cơ bản về nguyên hàm
Nguyên hàm là công cụ quan trọng để phân tích sự biến thiên của các hàm số. Nó giúp giải quyết các bài toán thực tế như diện tích, thể tích, và công việc. Hãy cùng tìm hiểu chi tiết về khái niệm này.
Khái niệm về nguyên hàm
Nguyên hàm là một hàm số mà khi tính đạo hàm, ta thu được hàm ban đầu. Khái niệm này có ứng dụng phổ biến trong nhiều lĩnh vực như toán học, vật lý và các ngành khoa học khác.
Xét hàm số y = f(x) xác định trên một tập A. Hàm F(x) được gọi là nguyên hàm của f(x) trên A nếu đạo hàm của F(x) thỏa mãn điều kiện F'(x) = f(x) với mọi x thuộc A.
Tập A có thể là một khoảng, nửa khoảng, đoạn hay nửa đoạn trên trục số R.
Họ nguyên hàm của f(x) là tập hợp vô số hàm số, mỗi hàm chỉ khác nhau bởi một hằng số, ký hiệu là ∫f(x) = F(x) + C, với C là một hằng số bất kỳ.

Định lý về nguyên hàm
Ba định lý cơ bản về nguyên hàm là cơ sở quan trọng của phép tính tích phân, giúp kết nối chặt chẽ giữa nguyên hàm và tích phân.
Định lý 1: Nếu F(x) là nguyên hàm của f(x), thì tồn tại vô số hàm số khác cũng là nguyên hàm của f(x), chỉ khác nhau ở một hằng số.

Định lý 2: Nếu F(x) là một nguyên hàm của hàm số f(x) trên khoảng K, thì mọi nguyên hàm khác của f(x) trong K có thể viết dưới dạng F(x) + C, với C là một hằng số tùy ý.
Định lý 3: Điều kiện liên tục của hàm f(x) trên khoảng K đảm bảo rằng nguyên hàm của nó tồn tại.
Công thức tính nguyên hàm cơ bản
Bảng công thức nguyên hàm là công cụ không thể thiếu cho những ai muốn nắm vững môn Toán cao cấp. Đây là kiến thức nền tảng giúp bạn tiếp cận các khái niệm phức tạp hơn trong giải tích và sử dụng máy tính để tìm nguyên hàm.

Để giải quyết các bài toán tích phân phức tạp, bạn cần nắm vững công thức đầy đủ. Bảng công thức nguyên hàm nâng cao sẽ cung cấp cho bạn các công cụ cần thiết để chinh phục những bài tập khó nhất.
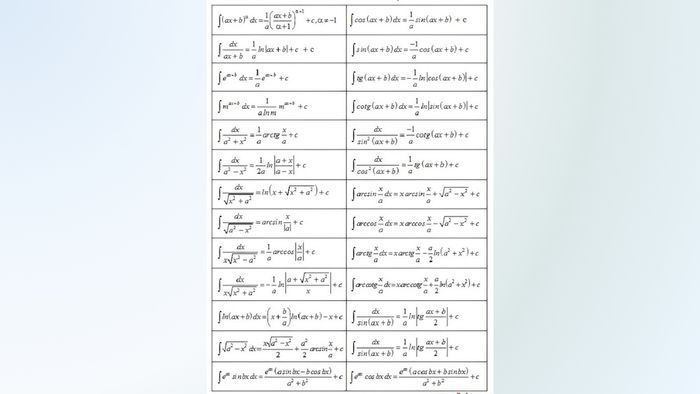
Với bảng công thức nguyên hàm cho hàm lượng giác, bạn sẽ khám phá những quy tắc đặc biệt của các hàm số lượng giác và tự tin sử dụng máy tính Casio 580 để tính nguyên hàm.

Hướng dẫn cách bấm máy tính tính nguyên hàm nhanh chóng và chính xác
Bạn muốn biết cách sử dụng máy tính Casio 580VN Plus để tính nguyên hàm? Mytour sẽ chỉ bạn từ cách nhập hàm vào máy cho đến cách đọc kết quả. Cùng khám phá các tính năng hữu ích của máy Casio 580 khi tính nguyên hàm.
Cách tìm nguyên hàm F(x) của hàm số f(x)
Nguyên hàm, mặc dù là một khái niệm có vẻ trừu tượng, nhưng lại đóng vai trò vô cùng quan trọng trong việc giải quyết các bài toán ứng dụng thực tế.
Bước 1: Chọn một giá trị x bất kỳ trong khoảng mà đề bài đã cung cấp (nếu có).

Bước 2: Tính đạo hàm của phương trình từ kết quả bài toán mà bạn đang kiểm tra.
Bước 3: Sau khi tính đạo hàm, bạn thực hiện phép trừ giữa giá trị mà đề bài cung cấp và kết quả đạo hàm vừa tính toán.
Bước 4: Kiểm tra kết quả thu được từ phép trừ.
Cách tìm nguyên hàm F(x) của hàm f(x) khi F(x0)=M
Chúng ta sẽ cùng tìm hiểu cách sử dụng máy tính để xác định nguyên hàm F(x) duy nhất thỏa mãn điều kiện đã cho.
Bước 1: Chọn một giá trị A bất kỳ và thay vào bài toán. Giá trị này có thể là một số thực mà bạn cho là phù hợp với bài toán.

Bước 2: Dựa trên giá trị x đã có, thực hiện tính toán nguyên hàm từ x đến A đã được xác định.
Bước 3: Thực hiện phép trừ giữa kết quả đề bài và giá trị nguyên hàm đã tính.
Bước 4: Kiểm tra và đánh giá kết quả của phép toán vừa thực hiện.
Hướng dẫn cách sử dụng máy tính để tính tích phân
Để tính tích phân trên máy tính, bạn cần tuân theo quy trình sử dụng máy tính 580VN Plus để đảm bảo độ chính xác trong các phép tính.
Bước 1: Đầu tiên, bạn cần tìm và chọn biểu tượng tích phân trên màn hình máy tính để bắt đầu quá trình tính toán.

Bước 2: Sau khi chọn biểu tượng tích phân, một ô nhập liệu sẽ xuất hiện trên màn hình. Tại đây, bạn cần nhập phương trình cần tính nguyên hàm.
Bước 3: Sau khi nhập phương trình, tiếp theo bạn cần nhập giá trị cận trên cho phép tích phân.
Bước 4: Nhập giá trị cận dưới vào ô vuông ngay dưới biểu thức hàm bạn vừa nhập xong.
Hướng dẫn cách tính diện tích hình phẳng và thể tích khối tròn xoay
Khi bạn đã thành thạo việc bấm máy tính nguyên hàm 580VN Plus trong các bài toán liên quan đến diện tích hình phẳng hay thể tích khối tròn xoay, bài toán sẽ được giải quyết nhanh chóng.
Bước 1: Đầu tiên, xác định công thức nguyên hàm cho diện tích hoặc thể tích cần tìm, sau đó nhập công thức này vào máy tính.

Bước 2: Sau khi có kết quả từ công thức tính, bạn lần lượt nhập các đáp án có sẵn vào máy tính.
Bước 3: Kiểm tra từng đáp án bạn đã nhập, xem nó có trùng với kết quả mà máy tính đã đưa ra hay không.
Bước 4: Cuối cùng, chọn đáp án có kết quả trùng khớp với kết quả máy tính tính toán sau khi kiểm tra tất cả các đáp án.
Bài tập ví dụ thực tế
Bạn đã nắm chắc cách sử dụng máy tính Casio FX 580 để tính nguyên hàm chưa? Bây giờ, chúng ta sẽ đi vào phần thực hành với những bài tập cụ thể. Những ví dụ này sẽ giúp bạn hiểu rõ hơn cách áp dụng lý thuyết để giải quyết các bài toán một cách chính xác và nhanh chóng.
Dạng 1: Tính nguyên hàm F(x) của hàm số f(x)

Dạng 2: Cách tìm nguyên hàm F(x) của hàm số f(x) khi F(x0)=M

Dạng 3: Hướng dẫn bấm máy tính để tính tích phân

Dạng 4: Hướng dẫn tìm diện tích hình phẳng và thể tích khối tròn xoay

Những lưu ý quan trọng khi giải bài tập về nguyên hàm
Để bấm máy tính nguyên hàm 580VN Plus, bạn cần có tư duy logic và phương pháp giải bài toán hợp lý.
- Hiểu rõ yêu cầu bài toán: Đọc kỹ đề bài để nắm bắt hàm số cần tích phân và các điều kiện ràng buộc.
- Áp dụng công thức chính xác: Sử dụng đúng phương pháp để tìm tích phân của hàm.
- Kiểm tra lại các bước tính toán: Đảm bảo các phép biến đổi và rút gọn đều chính xác.
- Nhớ thêm hằng số C: Đừng quên cộng thêm hằng số C vào kết quả cuối cùng của nguyên hàm.

Với cấu hình mạnh mẽ, bạn có thể dễ dàng tìm tài liệu và xem video hướng dẫn cách sử dụng máy tính 580VN Plus để tính nguyên hàm.
Chúng ta đã tìm hiểu xong cách tính nguyên hàm bằng máy tính Casio FX 580. Việc nắm vững kỹ năng này sẽ giúp bạn giải quyết nhanh chóng các bài tập và mở rộng khả năng học toán. Hãy luyện tập thường xuyên với máy tính 580VN Plus và chia sẻ kết quả nhé!
