Buzz
Dạng bài tập xác định phương trình tiếp tuyến cho đường tròn và đồ thị hàm số là một chủ đề quen thuộc trong các kỳ thi THPT. Đây là dạng bài toán khá dễ lấy điểm, vì vậy học sinh cần phải nắm vững kiến thức này để áp dụng hiệu quả trong bài thi. Sau đây, Mytour sẽ hướng dẫn các bạn phương pháp giải công thức phương trình tiếp tuyến để nâng cao kỹ năng giải toán của mình.
Ý nghĩa của phương trình tiếp tuyến đối với đồ thị hàm số
Đạo hàm của hàm số y = f(x) tại điểm x₀ có thể hiểu là hệ số góc của tiếp tuyến với đồ thị (C) tại điểm M(x₀, y₀), trong đó y₀ = f(x₀). Dựa vào điều này, phương trình của tiếp tuyến tại điểm M(x₀, y₀) sẽ có dạng sau:
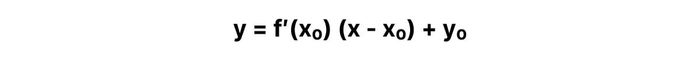
Để xác định phương trình tiếp tuyến, một bước không thể thiếu là bạn phải tìm ra hoành độ của điểm tiếp xúc x₀.
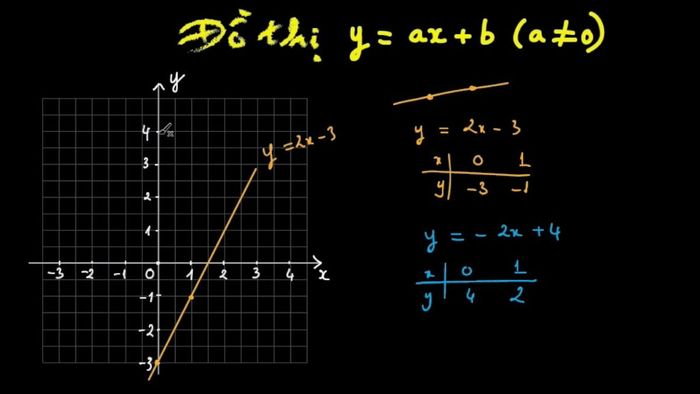
Các bài toán liên quan đến việc xác định phương trình tiếp tuyến
Mytour sẽ tổng hợp những dạng bài tập về phương trình tiếp tuyến của đường tròn và đồ thị các hàm số cơ bản mà bạn thường gặp. Hãy tham khảo để có thể linh hoạt vận dụng vào các bài tập của mình nhé:
Viết phương trình tiếp tuyến tại điểm M(x₀,y₀)
Giả sử bài toán cho đồ thị (C) : y = f(x) và yêu cầu xác định phương trình tiếp tuyến tại điểm M(x₀,y₀). Bạn sẽ cần thực hiện theo hai bước sau:
- Bước 1: Tính đạo hàm của hàm số y’ = f(x) để xác định hệ số góc tiếp tuyến k = y'(x₀).
- Bước 2: Xác định phương trình tiếp tuyến tại M(x₀,y₀) theo công thức:
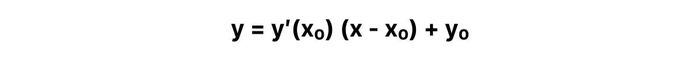
Chú ý:
- Khi đề bài đã cho hoành độ tiếp điểm x₀, bạn chỉ cần thay x₀ vào hàm số ban đầu để tính tung độ y₀, tức là y₀ = f(x₀).
- Nếu đề bài cho tung độ tiếp điểm y₀, bạn có thể tính giá trị x bằng cách thay y₀ vào phương trình hàm số và giải phương trình f(x₀) = y₀ để tìm x₀.
- Nếu bài toán yêu cầu xác định phương trình tiếp tuyến tại các điểm giao nhau giữa đồ thị (C): y = f(x) và đường thẳng (d): y = ax + b, bạn cần giải phương trình xác định giao điểm giữa (C) và (d) để tìm các hoành độ của tiếp điểm.
Để học tốt về phương trình tiếp tuyến và giải các bài toán nhanh chóng, bạn có thể đến Mytour để lựa chọn một chiếc máy tính chất lượng. Với mức giá hợp lý và chế độ bảo hành chính hãng, sản phẩm máy tính tại Mytour sẽ hỗ trợ bạn học hiệu quả. Hãy tham khảo những chiếc máy tính tốt nhất tại đây cùng Mytour nhé:
Viết phương trình tiếp tuyến khi đã biết hệ số góc k
Khi đề bài cho y = f(x) với đồ thị (C) và yêu cầu bạn tìm phương trình tiếp tuyến Δ với hệ số góc k đã cho, bạn cần thực hiện theo các bước sau:
Bước 1: Xác định tiếp điểm M(x₀, y₀) trên đồ thị và tính đạo hàm f’(x) của hàm số y = f(x).
Bước 2: Điều kiện để tiếp tuyến có hệ số góc k là f’(x₀) = k. Khi đó, bạn cần giải phương trình này để tìm x₀ và tính y₀ = f(x₀).
Lưu ý:
- Tiếp tuyến d song song với Δ : y = ax + b ⇒ k = a
Sau khi xác định phương trình tiếp tuyến, bạn cần kiểm tra lại để chắc chắn rằng tiếp tuyến không trùng với đường thẳng Δ. Nếu có sự trùng nhau, kết quả đó cần được loại bỏ.
- Khi tiếp tuyến d vuông góc với Δ:
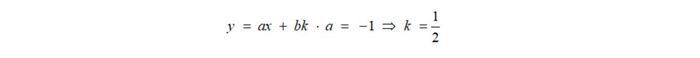
- Nếu tiếp tuyến tạo một góc α với trục hoành, hệ số góc sẽ được tính bằng k = ± tan(α).
Tổng quát: Tiếp tuyến tạo một góc α với đường thẳng Δ : y = ax + b.
Khi đó:
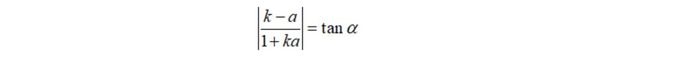
Viết phương trình tiếp tuyến đi qua một điểm
Đề bài yêu cầu xác định phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến phải đi qua điểm A(xₐ, yₐ) đã cho. Lúc này, bạn cần áp dụng hai cách giải dưới đây:
Cách 1:
Bước 1: Phương trình tiếp tuyến đi qua điểm A(xₐ, yₐ) với hệ số góc k được viết dưới dạng d: y = k(x - xₐ) + yₐ.
Bước 2: Để đường thẳng d tiếp xúc với (C), hệ phương trình dưới đây cần có nghiệm:
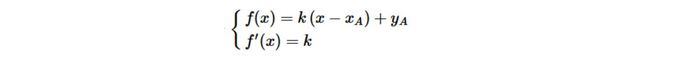
Bước 3: Giải hệ phương trình đã cho để xác định giá trị của x và k. Sau đó, thay các giá trị này vào phương trình d: y = k(x - xₐ) + yₐ để tìm phương trình tiếp tuyến cần xác định.
Cách 2:
Bước 1: Giả sử tiếp điểm có tọa độ M(x₀, f(x₀)), lúc này bạn xác định hệ số góc của tiếp tuyến k = f′(x₀) dựa vào giá trị của x₀.
Bước 2: Khi đó, phương trình của tiếp tuyến sẽ được viết dưới dạng d : y = f′(x₀) (x − x₀) + f(x₀).
Đồng thời, vì điểm A(xₐ, yₐ) nằm trên đường thẳng d nên ta có: yₐ = f′(x₀) (xₐ − x₀) + f(x₀). Lúc này, bạn cần giải phương trình vừa rồi để xác định giá trị của x₀.
Bước 3: Sau khi tìm được giá trị của x, bạn hãy thay vào phương trình d : y = f′(x₀) (x − x₀) + f(x₀) để tìm được phương trình tiếp tuyến.
Bài tập vận dụng
Sau khi đã tìm hiểu các công thức phương trình tiếp tuyến của đồ thị hàm số, bạn hãy tiếp tục vận dụng kiến thức mình vừa học để giải thử những bài toán liên quan dưới đây. Mỗi dạng bài tập này sẽ giúp bạn nắm thật vững công thức để đạt điểm số cao hơn nhé:
Bài tập 1
Đề bài: Viết công thức phương trình tiếp tuyến của đồ thị hàm số y = x³ - 3x² + 2 tại điểm M(2,2).
Lời giải: Ta có y’ = 3x² - 6x => k = y’(2) = 3(2)² - 6(2) = 12 - 2 = 0.
Lúc này, phương trình tiếp tuyến bạn cần tìm sẽ có dạng: y - y₀ = k(x - x₀) ⇔ y - 2 = 0(x - 2) => y = 2.
Bài tập 2
Đề bài: Viết công thức phương trình tiếp tuyến của đồ thị (C) : y = x³ - 3x + 2 với hệ số góc là 9.
Lời giải: Ta có y′ = 3x² - 3 và xác định điểm tiếp tuyến M(x₀, y₀)
=> Hệ số góc tiếp tuyến là k= y′ (x₀) = 9, suy ra:
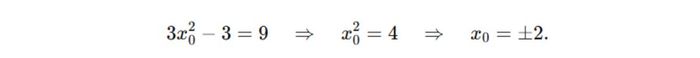
Với x₀ = 2, ta có y₀ = 4, tiếp điểm M1(2;4). Như vậy, phương trình tiếp tuyến tại M1 là:
y = 9(x - 2) + 4 ⇒ y = 9x - 14.
Với x₀ = -2, ta có y₀ = 0, tiếp điểm M2(-2;0). Lúc này, phương trình tiếp tuyến tại M2 là:
y = 9(x + 2) ⇒ y = 9x + 18.
Kết luận: Hai phương trình tiếp tuyến mà ta cần tìm là:
d1 : y = 9x -14 và d2 : y = 9x + 18.
Bài tập 3
Đề bài: Cho hàm số y = 3x² - 4x² với đồ thị (C), tìm phương trình tiếp tuyến tại điểm trên đồ thị (C) sao cho tiếp tuyến đó đi qua điểm A(1;3).
Lời giải: Đạo hàm của hàm số y′ = 3 - 8x, đây chính là hệ số góc của tiếp tuyến tại điểm M(x₀; y₀).
Vì vậy, phương trình của tiếp tuyến tại M(x₀; y₀) có thể viết dưới dạng:
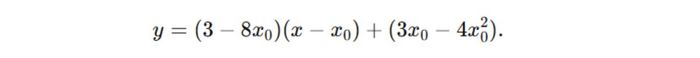
Dựa trên điều kiện tiếp tuyến đi qua điểm A(1;3), ta có phương trình tiếp tuyến như sau:
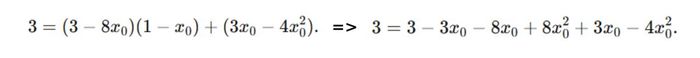
Do đó, x₀ có thể là 0 hoặc 2.
Khi x₀ = 0, ta tính được: y(0) = 3(0) - 4(0)² = 0 và đạo hàm tại x₀, y′(0) = 3 - 8(0) = 3.
Vậy, phương trình tiếp tuyến tại M(0;0) là y = 3(x - 0) + 0 = 3x.
Với x₀ = 2, ta có: y(2) = 3(2) - 4(2)² = 6 - 16 = -10 và y′(2) = 3 - 8(2) = 3 - 16 = -13.
Khi đó, phương trình tiếp tuyến tại M(2;-10) cần tìm là:
y = -13(x - 2) - 10 = -13x + 26 - 10 = -13x + 16.
Kết luận: Hai phương trình tiếp tuyến cần tìm là: y = 3x và y = -13x + 16.
Mytour đã giúp bạn tìm hiểu cách thức viết công thức phương trình tiếp tuyến của đường tròn và đồ thị hàm số lớp 11. Hy vọng qua bài viết này, các bạn đã nắm vững cách giải các dạng toán liên quan đến phương trình tiếp tuyến của đồ thị hàm số để đạt được điểm cao nhất. Đừng quên truy cập Mytour để tìm hiểu thêm nhiều công thức hữu ích khác nhé!
- Xem thêm các bài viết thú vị tại chuyên mục: Giáo dục; Góc Học & Day 4.0.
