Công thức Delta và Delta phẩy là những công thức cơ bản và quan trọng trong việc giải phương trình bậc hai. Vậy công thức này có tác dụng gì trong việc tìm nghiệm và cách áp dụng nó hiệu quả vào các bài tập?

Trong toán học, đặc biệt là đại số, công thức delta đóng vai trò cực kỳ quan trọng khi giải phương trình bậc hai. Công thức này giúp xác định số lượng nghiệm của phương trình và tìm ra nghiệm cụ thể. Để áp dụng công thức delta phẩy vào các bài tập, chúng ta cần biết cách sử dụng đúng đắn. Hãy cùng Mytour khám phá kiến thức này!

Khái niệm về Delta và phương trình bậc hai với một ẩn

Để giải phương trình bậc hai, chúng ta cần vận dụng công thức nghiệm delta phẩy và delta. Đây là dạng bài thường xuyên xuất hiện trong các kỳ thi của học sinh trung học cơ sở. Trước khi bắt tay vào công thức, chúng ta cần củng cố lý thuyết cơ bản về phương trình bậc hai này.

Delta và Delta phẩy là những khái niệm cơ bản trong giải phương trình bậc hai. Vậy chúng có ý nghĩa gì và cách áp dụng chúng thế nào?

Delta (ký hiệu: Δ) là một trong những chữ cái nổi bật trong bảng chữ Hy Lạp cổ đại. Trong toán học, công thức delta trong phương trình bậc hai giúp xác định số nghiệm một cách nhanh chóng và hiệu quả. Bên cạnh đó, ký hiệu này còn được sử dụng trong nhiều lĩnh vực khác nhau.

Delta phẩy (ký hiệu: Δ') là dạng biến thể của delta được sử dụng khi giải phương trình. Công thức này giúp đơn giản hóa và rút ngắn quá trình giải quyết một số bài toán đặc biệt, làm cho việc tính toán trở nên dễ dàng và nhanh chóng hơn.

Tại sao việc tính delta lại quan trọng trong việc giải phương trình bậc hai?

Mục đích của việc tính delta là xác định chính xác số lượng nghiệm trong phương trình. Ngoài ra, phương pháp này còn giúp phân tích đặc điểm của nghiệm và vẽ đồ thị hàm số. Giá trị delta cho biết tính chất của nghiệm theo các trường hợp cụ thể.

Việc áp dụng công thức delta phẩy làm cho việc giải bài tập trở nên dễ dàng hơn rất nhiều. Ngoài việc ghi chép công thức, sử dụng máy tính bảng giúp lưu trữ nhanh chóng và thuận tiện. Với màn hình rộng và dung lượng lớn, đây là công cụ hữu ích hỗ trợ trong quá trình học tập của bạn.

Phương trình bậc hai một ẩn là một phương trình có dạng ax² + bx + c = 0, trong đó a, b, c là các hệ số và x là ẩn cần tìm.

Đây là một trong những kiến thức quan trọng cần phải nắm vững để chuẩn bị tốt cho kỳ thi tuyển sinh lớp 10. Phương trình bậc hai có dạng tổng quát như sau:

ax2 + bx + c = 0 (với a khác 0)

Trong đó:

• x: ẩn số trong phương trình
• a, b: các hệ số của phương trình
• c: hằng số

Dưới đây là một số ví dụ giúp bạn dễ dàng hiểu hơn khi áp dụng công thức vào các bài toán:

Phương trình x² - 5x + 4 = 0 với a = 1; b = -5; c = 4.

Phương trình -3x² + 2x - 4 = 0 với a = -3; b = 2; c = -4.

Phương trình 12x² + 34x = 0 với a = 12; b = 34 và c = 0.

Công thức Delta và Delta phẩy trong việc giải phương trình bậc hai một ẩn

Biệt thức , ’ có dạng:

• Công thức delta: = b2 - 4ac.
• Công thức delta phẩy: ’ = b’2 - ac và b = 2b’.

Khi làm bài tập, ta cần áp dụng một trong hai công thức nghiệm delta sau đây:

Đối với biệt thức delta () = b2 - 4ac:

• Trường hợp > 0, phương trình (PT) có 2 nghiệm phân biệt: x1=-b+2a ; x2=-b-2a.
• Trường hợp = 0, PT có nghiệm kép: x1=x2=-b2a.
• Trường hợp < 0, PT không tồn tại nghiệm.

Khi a và c có dấu trái ngược nhau, delta lớn hơn 0 và phương trình sẽ có hai nghiệm phân biệt.

Đối với biệt thức delta phẩy, công thức là ’ = b’² - ac và b = 2b’:

• Khi ’ > 0, phương trình có hai nghiệm phân biệt: x1 = -b’ + a ; x2 = -b’ - a.
• Khi ’ = 0, phương trình có nghiệm kép: x1 = x2 = -b’ / 2a.
• Khi ’ < 0, phương trình không có nghiệm.

Chúng ta thường tự hỏi vì sao cần phải tính delta, dưới đây là phần giải thích và chứng minh cho công thức này:

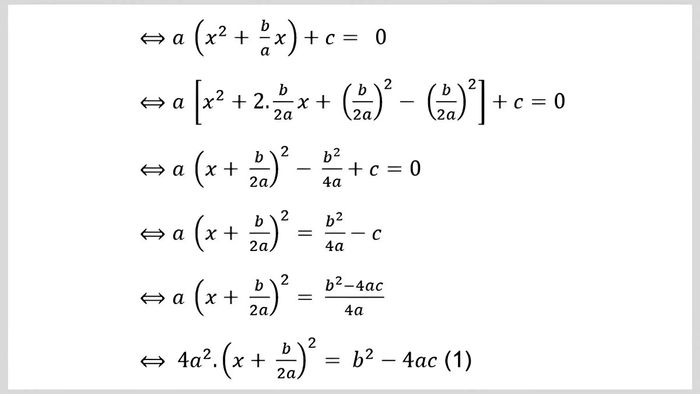
Chúng ta nhận thấy rằng, phần vế phải đã được chứng minh từ phương trình. Và do 4a² > 0, a ≠ 0 và x + b² / 2a > 0, từ đó suy ra vế trái luôn dương. Chính vì vậy, cần phải biện luận nghiệm của biểu thức b² - 4ac.

Bảng tổng hợp các nghiệm của phương trình bậc hai

Dưới đây là bảng tóm tắt các công thức nghiệm delta khi tính biệt thức, hỗ trợ bạn trong quá trình giải bài tập phương trình bậc hai.

Các dạng bài tập áp dụng công thức Delta và Delta phẩy

Để hiểu rõ lý thuyết về delta, bạn cần thực hành qua các bài tập cụ thể. Các bài tập dưới đây được phân thành hai dạng chính, giúp bạn dễ dàng củng cố kiến thức và phân biệt rõ các dạng bài. Học thuộc các công thức nghiệm delta sẽ giúp bạn giải quyết các bài tập nhanh chóng và chính xác.

Giải phương trình bậc hai với một ẩn

Với dạng bài này, bạn cần áp dụng công thức delta và delta phẩy để giải. Thêm vào đó, việc nắm vững các công thức nghiệm delta trong từng trường hợp sẽ giúp bạn giải bài tập một cách hiệu quả hơn.

Bài tập:

a) 3x² + 5x - 2 = 0

Áp dụng công thức delta, ta có: Δ = b² - 4ac = 5² - 4.3.(-2) = 49 > 0

⇒ Phương trình có 2 nghiệm.

x₁ = -b + √Δ / 2a = -5 + √49 / 2.3 = 13 ; x₂ = -b - √Δ / 2a = -5 - √49 / 2.3 = -2

b) 5x² - 6x + 1 = 0

Áp dụng công thức delta phẩy, ta có: b' = b² = (-6)² = 36

Δ' = b'² - ac = (–3)² - 5.1 = 4 > 0

⇒ Phương trình có 2 nghiệm phân biệt:

x₁ = -b' + √Δ' / a = -(-3) + √4 / 5 = 1 ; x₂ = -b' - √Δ' / a = -(-3) - √4 / 5 = 15

Tương tự như cách giải trước đó, bạn hãy thử sức với các bài tập dưới đây để rèn luyện kỹ năng nhé:

Phân tích và biện luận nghiệm phương trình bậc hai một ẩn

Đây là dạng bài có độ khó cao hơn so với việc giải phương trình đơn giản. Do đó, khi giải bài tập này, chúng ta cần hiểu vững kiến thức cơ bản để xác định đúng công thức nghiệm delta phù hợp.

Ví dụ:

Giải và phân tích nghiệm phương trình: x2 - 2m + 1 + 2m + 10 = 0

Áp dụng công thức delta phẩy, ta có: b' = b2 = -2(m + 1)2 = -(m + 1)

’ = b’2 - ac = (m + 1)2 - 2m + 10 = m2 - 9

Nếu ’ > 0 ⟺ m2 - 9 > 0 ⟺ m < -3 hoặc m > 3. Phương trình có 2 nghiệm phân biệt:

x1 = -b' + ' a = --(m + 1) + m2 - 91 = m + 1 + m2 - 9 ; x2 = -b' - ' a = --(m + 1) - m2 - 91 = m + 1 - m2 - 9

Nếu ’ = 0 ⟺ m = 3

Với m = 3, phương trình có nghiệm x1,2 = -ba = --(m + 1)1 = --(3 + 1)1 = 4.

Với m = -3, phương trình có nghiệm x1,2=-ba=--(m + 1)1=--(-3 + 1)1=-2.

Nếu ’ < 0 ⟺ -3 < m < 3, phương trình vô nghiệm.

Ứng dụng các công thức tính delta phẩy, delta để giải một số bài tập sau:

Hãy giải và biện luận các phương trình: 

Mytour đã giúp bạn tổng hợp các công thức delta, tính delta phẩy. Đồng thời, bài viết cũng gợi ý cho chúng ta một số bài tập áp dụng công thức nghiệm delta. Hy vọng bài viết này sẽ giúp các bạn học sinh có điểm số tốt ở các kỳ thi sắp tới. Đừng quên cập nhật các kiến thức toán học tại Mytour nhé.