Diện tích hình lập phương là một khái niệm quan trọng trong hình học không gian, giúp chúng ta nắm bắt được các đặc điểm và tính chất của hình khối này. Việc làm chủ công thức tính diện tích toàn phần và diện tích xung quanh của hình lập phương sẽ giúp bạn giải quyết nhanh chóng các bài toán hình học. Cùng Mytour tìm hiểu chi tiết về các công thức này và các ứng dụng của chúng trong bài tập thực tế.
Hình lập phương là gì?
Hình lập phương là một hình khối đặc biệt trong không gian, có ba chiều dài, rộng và cao đều bằng nhau. Nó là một khối hình học có 6 mặt vuông góc đều nhau, mỗi mặt là một hình vuông có kích thước giống hệt nhau. Hình lập phương cũng là một dạng hình chữ nhật đặc biệt, trong đó tất cả các cạnh đều có độ dài như nhau.

Những đặc điểm của hình lập phương càng làm nổi bật tính độc đáo của nó, với 8 mặt đối xứng, 12 cạnh đồng đều, 8 đỉnh và ba cạnh gặp nhau tại mỗi đỉnh. Đặc biệt, hình lập phương còn có bốn đường chéo giao nhau tại một điểm duy nhất, nơi mà giao điểm này trở thành tâm đối xứng của khối. Những đường chéo này không chỉ gặp nhau tại trung tâm mà còn có chiều dài bằng nhau, tạo nên sự đối xứng hoàn hảo cho hình lập phương.
Khi nghiên cứu về diện tích hình lập phương, đặc biệt là diện tích toàn phần và diện tích xung quanh, một chiếc laptop mạnh mẽ sẽ là công cụ rất hữu ích để giải quyết các bài tập một cách hiệu quả. Laptop với các phần mềm tính toán, bảng tính và công cụ vẽ hình học sẽ giúp bạn hình dung tốt hơn các khái niệm, cũng như áp dụng dễ dàng các công thức vào bài tập thực tế. Lựa chọn một chiếc laptop có cấu hình mạnh mẽ sẽ đáp ứng nhu cầu học tập và nghiên cứu tối ưu.
Công thức tính diện tích toàn phần của hình lập phương
Công thức tính diện tích toàn phần của hình lập phương có vẻ đơn giản, nhưng lại vô cùng quan trọng trong việc giải quyết các bài toán hình học không gian. Hình lập phương với đặc điểm nổi bật là sáu mặt vuông đều, tạo nên một cấu trúc cân đối. Diện tích toàn phần của nó được tính bằng cách cộng tổng diện tích của từng mặt, từ đó giúp ta hiểu rõ hơn về khối này và khám phá những ứng dụng thực tiễn hữu ích.
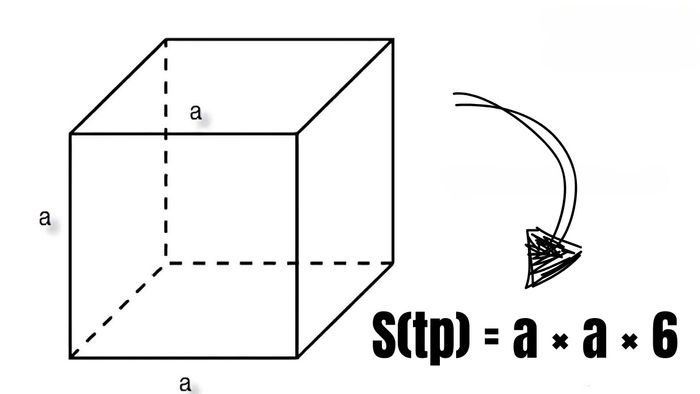
Dưới đây là công thức để tính diện tích toàn phần của hình lập phương:
S(tp) = a × a × 6
Trong công thức này, a đại diện cho chiều dài của một cạnh của hình lập phương, là yếu tố chính để xác định kích thước của khối hình học này. Diện tích toàn phần của hình lập phương được ký hiệu là S(tp), chính là giá trị mà ta cần tìm trong quá trình tính toán.
Công thức tính diện tích xung quanh của hình lập phương
Diện tích xung quanh khác biệt với diện tích toàn phần ở chỗ nó chỉ tính tổng diện tích của bốn mặt bên, bỏ qua hai mặt đáy và đỉnh. Để tính diện tích xung quanh, chúng ta bắt đầu từ diện tích của một mặt, được tính bằng cạnh bình phương, sau đó nhân kết quả này với 4 vì hình lập phương có bốn mặt xung quanh giống nhau.
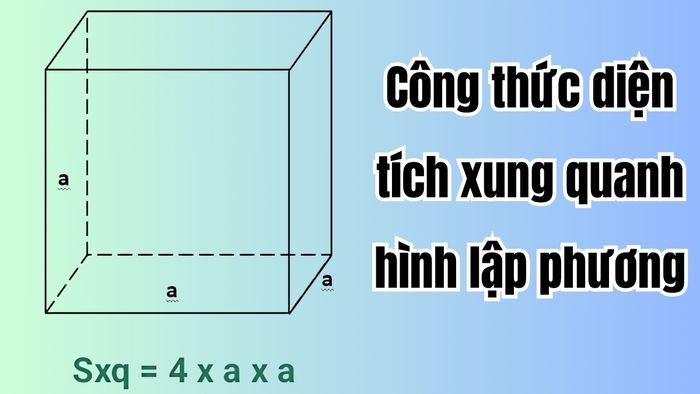
Cụ thể, diện tích xung quanh của hình lập phương được tính theo công thức đơn giản như sau:
S(xq) = a × a × 4
Ở đây, a đại diện cho độ dài của một cạnh của hình lập phương, là yếu tố quan trọng tác động trực tiếp đến diện tích của khối hình này. S(xq) là diện tích xung quanh của hình lập phương, giá trị cần tính để hiểu rõ hơn về tổng diện tích của các mặt bên của khối.
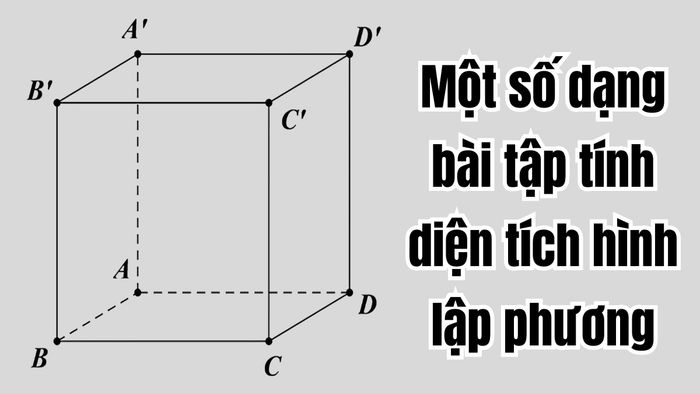
Một số dạng bài tập tính diện tích hình lập phương
Dưới đây là một số bài tập được thiết kế nhằm giúp bạn áp dụng công thức tính diện tích toàn phần và xung quanh của hình lập phương vào các tình huống thực tế:
Bài 1: Cho hình lập phương ABCDEF có chiều dài cạnh là 5 cm. Bài toán yêu cầu bạn áp dụng các công thức hình học để tính diện tích xung quanh S(xq) và diện tích toàn phần S(tp) của hình khối này.
Đáp án:
Để tính diện tích xung quanh, áp dụng công thức sau: S(xq) = 5 × 5 × 4 = 125 cm²
Tiếp theo, để tìm diện tích toàn phần, chúng ta sử dụng công thức: S(tp) = 5 × 5 × 6 = 150 cm²
Bài 2: Bài toán yêu cầu bạn tính diện tích xung quanh S(xq) và diện tích toàn phần S(tp) của hình lập phương có chiều dài cạnh là 11 cm.
Đáp án:
Diện tích xung quanh: S(xq) = 11 × 11 × 4 = 484 cm²
Diện tích toàn phần: S(tp) = 11 × 11 × 6 = 726 cm²
Bài 3: Giả sử bạn làm một chiếc hộp bằng tôn không nắp có dạng lập phương với chiều dài cạnh là 9 cm, hãy tính diện tích miếng tôn cần dùng để chế tạo hộp.
Đáp án:
Diện tích tôn cần dùng để làm hộp là: 9 × 9 × 5 = 405 cm²
Bài 4: Lan đã dán giấy màu lên các mặt của một chiếc hộp quà lập phương có chiều dài cạnh là 4 cm. Câu hỏi là diện tích giấy Lan đã sử dụng để dán lên hộp là bao nhiêu?
Đáp án:
Diện tích giấy mà Lan đã dán là: 4 × 4 × 6 = 96 cm²
Thông qua bài viết này, hy vọng bạn đã hiểu rõ công thức tính diện tích hình lập phương toàn phần và diện tích xung quanh của hình lập phương. Kiến thức về diện tích hình lập phương không chỉ giúp bạn giải quyết bài tập hình học, mà còn có thể ứng dụng vào nhiều tình huống thực tiễn trong cuộc sống. Việc nắm vững các công thức này sẽ hỗ trợ bạn trong việc giải quyết các vấn đề hàng ngày một cách chính xác và hiệu quả hơn.
