Trong toán học, khái niệm đa thức rất quan trọng trong các bài toán từ cơ bản đến nâng cao. Bậc của đa thức là gì trong lớp 8 – đây là yếu tố giúp xác định mức độ của một đa thức, phản ánh số mũ lớn nhất của biến trong biểu thức. Ngoài ra, việc rút gọn đa thức là gì cũng là bước quan trọng giúp học sinh đơn giản hóa các biểu thức toán học, phát triển tư duy logic và chuẩn bị nền tảng cho các kiến thức nâng cao.
Đa thức là gì?
Trong toán học, đa thức là biểu thức đại số được hình thành từ tổng của nhiều đơn thức. Mỗi đơn thức trong đa thức có thể bao gồm biến và hệ số, được kết nối với nhau bằng phép cộng hoặc trừ.
Tiếp theo, chúng ta sẽ tìm hiểu về bậc của đa thức. Bậc của đa thức được xác định qua số mũ lớn nhất của biến trong các hạng tử. Đây là yếu tố then chốt giúp nhận diện tính chất và cách giải quyết một đa thức trong các bài toán thực tế.
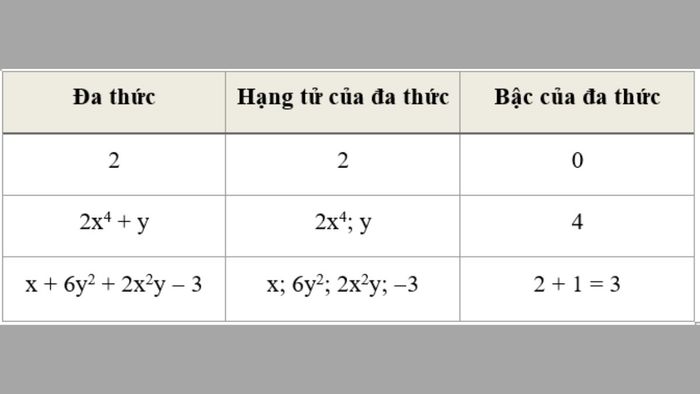
Khi làm việc với đa thức, việc thu gọn chúng là rất quan trọng để biểu thức trở nên gọn gàng và dễ hiểu hơn. Thu gọn đa thức là gì? Quá trình này bao gồm việc nhóm các hạng tử giống nhau lại, giúp đơn giản hóa biểu thức, từ đó việc tính toán trở nên dễ dàng hơn.
Với những kiến thức trên, học sinh lớp 8 sẽ hiểu rõ hơn về đa thức là gì trong chương trình lớp 8, đồng thời học cách xử lý và biến đổi biểu thức một cách linh hoạt.
Các phép toán với đa thức
Đa thức không chỉ được biểu diễn mà còn có thể tham gia vào nhiều phép toán khác nhau. Hiểu rõ đa thức là gì và làm quen với ví dụ sẽ giúp bạn nắm vững cách áp dụng các phép toán với đa thức, từ đó đơn giản hóa biểu thức và giải quyết các bài toán quan trọng.
Cộng và trừ đa thức
Cộng và trừ đa thức là quá trình kết hợp hoặc loại bỏ các hạng tử đồng dạng để làm gọn biểu thức. Khi thực hiện, ta sẽ nhóm các hạng tử có cùng biến và số mũ, sau đó tính tổng hoặc hiệu của các hệ số tương ứng.

Ví dụ:
Cho hai đa thức:
𝑃(𝑥) = 3x2 + 5x - 2 và Q(𝑥) = -x2 + 4x + 3
Ta có:
𝑃(𝑥) + Q(𝑥) = (3x2 - x2) + (5x + 4x) + (-2 + 3) = 2x2 + 9x + 1
Nhân hai đa thức
Nhân hai đa thức là quá trình sử dụng quy tắc phân phối để nhân từng hạng tử của một đa thức với từng hạng tử của đa thức còn lại. Sau khi thực hiện phép nhân, ta sẽ nhóm các hạng tử đồng dạng lại để làm rõ biểu thức đa thức, kèm theo ví dụ cụ thể.
Ví dụ:
Cho 𝑃(𝑥) = 2x + 3 và Q(𝑥) = x - 4
Kết quả phép nhân:
𝑃(𝑥) x Q(𝑥) = (2x ⋅ x) + (2x ⋅ -4) + (3 ⋅ x) + (3 ⋅ -4) = 2x2 - 8x + 3x - 12 = 2x2 - 5x - 12
Chia đa thức cho đơn thức
Chia đa thức cho đơn thức là quá trình thực hiện phép chia từng hạng tử của đa thức cho đơn thức, sau đó rút gọn kết quả. Sau khi chia, ta phân tích và đơn giản hóa từng hạng tử, giúp làm rõ khái niệm đa thức thông qua ví dụ trực quan và dễ hiểu, giúp việc tính toán trở nên dễ dàng hơn.

Ví dụ:
Cho đa thức 𝑃(𝑥) = 6x2 + 9x và đơn thức 𝐷(𝑥) = 3x
Kết quả phép chia:
(6x2 + 9x)/ 3x = 6x2/ 3x + 9x/ 3x = 2x + 3
Bài tập ví dụ về đa thức có lời giải
Giải quyết các bài tập về đa thức giúp bạn hiểu sâu hơn về các phép toán và cách áp dụng chúng trong việc giải bài toán cụ thể. Điều này giúp bạn thành thạo trong việc làm việc với đa thức, từ các phép cộng, trừ, nhân, chia, đến các phương pháp rút gọn và phân tích biểu thức.
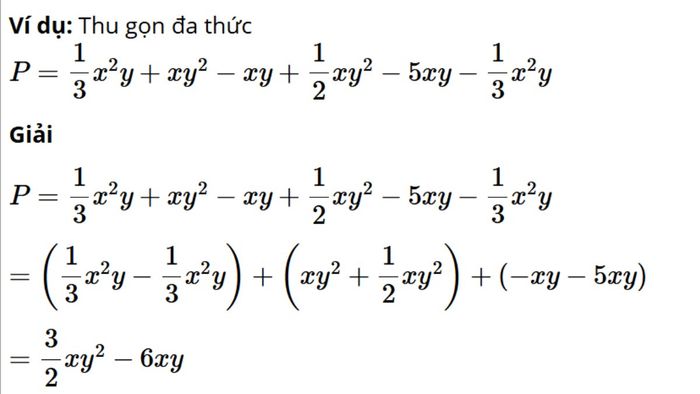

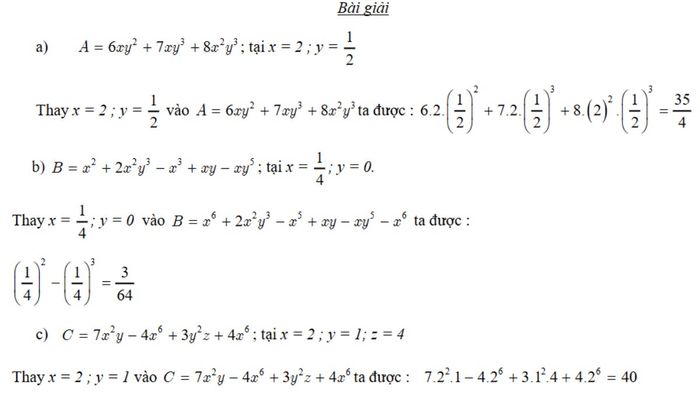
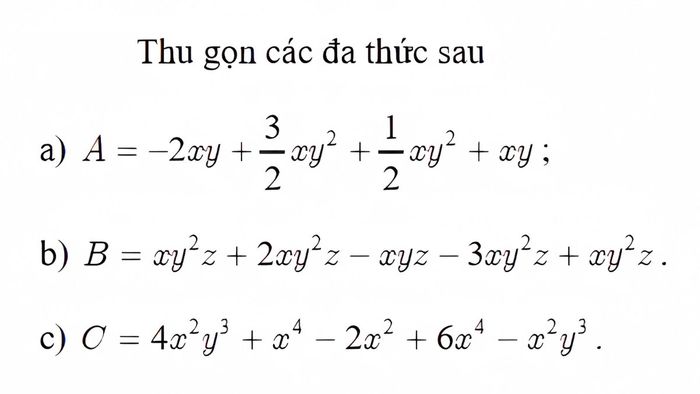
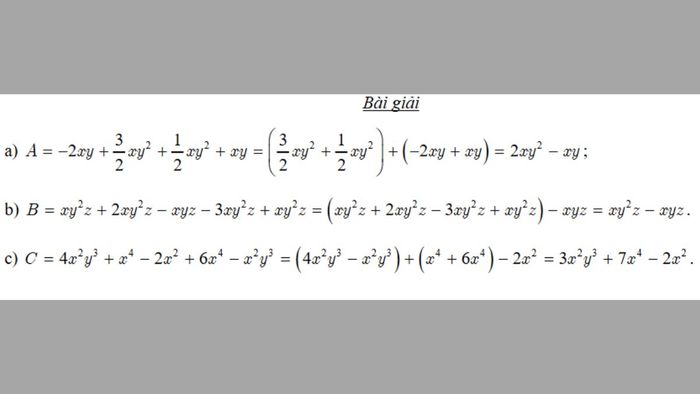
Áp dụng lý thuyết vào thực tế, học sinh sẽ dễ dàng nhận diện và giải quyết các dạng bài tập về đa thức một cách chính xác và hiệu quả.
Nắm vững kiến thức về đa thức không chỉ giúp bạn giải toán nhanh chóng mà còn tăng cường khả năng tư duy toán học có hệ thống. Hiểu rõ về bậc của đa thức sẽ giúp bạn dễ dàng phân loại và xử lý các bài toán liên quan đến phương trình, bất phương trình. Đồng thời, thành thạo việc thu gọn đa thức sẽ giúp bạn thực hiện các phép biến đổi biểu thức chính xác và nhanh chóng, làm chủ kỹ năng giải toán hiệu quả.
