Dấu của tam thức bậc hai là một phần kiến thức trọng yếu trong đại số, giúp xác định các khoảng giá trị của hàm số và giải các bài toán liên quan đến bất phương trình bậc hai. Hiểu rõ cách xét dấu không chỉ hỗ trợ học sinh trong học tập mà còn là công cụ thiết thực khi áp dụng vào các vấn đề thực tiễn. Bài viết dưới đây từ Mytour sẽ cung cấp hướng dẫn chi tiết về cách xét dấu tam thức bậc hai để bạn tham khảo.
Khái niệm về tam thức bậc hai
Tam thức bậc hai là một biểu thức toán học có thể được biểu diễn dưới dạng tổng quát như sau:
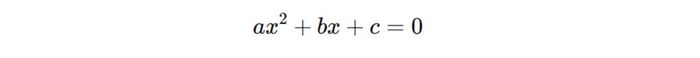
Trong đó, a, b, c là các hằng số với điều kiện a ≠ 0 và x là biến số.
Tam thức bậc hai xuất hiện rộng rãi trong nhiều ngành toán học, từ đại số đến hình học, cũng như trong các ứng dụng thực tế như vật lý, kinh tế và kỹ thuật. Đặc điểm nổi bật của nó là bậc cao nhất là bậc hai, tạo ra đồ thị parabol khi được biểu diễn trên hệ trục tọa độ.
Để xác định hình dạng và vị trí của một parabol, cần phân tích các hệ số a, b và c trong phương trình. Cụ thể, dấu của hệ số a quyết định hướng mở của parabol: mở lên trên nếu a > 0 và mở xuống dưới nếu a < 0. Nghiên cứu tam thức bậc hai không chỉ giúp giải phương trình mà còn hỗ trợ tìm cực trị, phân tích dấu của biểu thức và áp dụng vào các bài toán thực tế.

Hiện nay, Google cung cấp rất nhiều bài tập trực tuyến giúp bạn áp dụng tối đa lý thuyết vào các dạng bài về tam thức bậc hai. Một chiếc laptop dành cho sinh viên chắc chắn là công cụ hỗ trợ không thể thiếu. Hãy ghé ngay cửa hàng Mytour để chọn mua mẫu laptop phù hợp nhất và nhận những ưu đãi hấp dẫn!
Khái niệm về dấu của tam thức bậc hai lớp 10
Trong toán học, dấu của tam thức bậc hai lớp 10 thể hiện sự thay đổi của biểu thức này trên trục số thực. Xét tam thức bậc hai dưới dạng tổng quát:
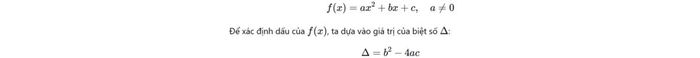
Xét từng trường hợp cụ thể:


Hướng dẫn chi tiết cách xét dấu tam thức bậc hai
Việc xét dấu của tam thức bậc hai là bước quan trọng trong giải toán, giúp xác định các khoảng giá trị mà biểu thức mang dấu dương hoặc âm. Để thực hiện, chúng ta áp dụng định lý về dấu của tam thức bậc hai theo các bước sau:
Bước 1: Tam thức bậc hai có dạng tổng quát như sau:
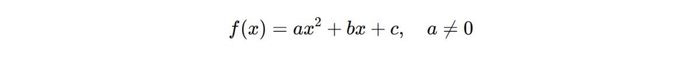
Tính biệt thức ∆ bằng công thức:
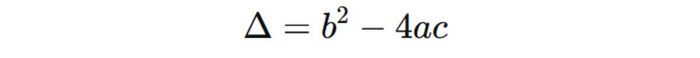
Bước 2: Dấu của ∆ xác định số nghiệm của phương trình f(x) = 0, từ đó ảnh hưởng đến việc xét dấu của tam thức bậc hai trong chương trình lớp 10.
- Nếu Δ > 0, phương trình có hai nghiệm phân biệt x1 và x2.
- Nếu Δ = 0, phương trình có nghiệm kép x0.
- Nếu Δ < 0, phương trình vô nghiệm.
Bước 3:
Hệ số a xác định hướng của parabol:
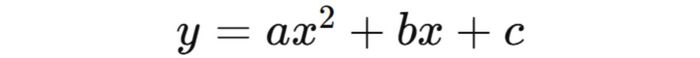
- Nếu a > 0, parabol có bề lõm hướng lên và nhánh đi lên.
- Nếu a < 0, parabol có bề lồi hướng xuống và nhánh đi xuống.
Bước 4:
Chúng ta sẽ áp dụng định lý về dấu của tam thức bậc hai như một phương pháp hiệu quả để giải quyết các bài toán liên quan.
- Khi Δ > 0, dấu của f(x) thay đổi tại hai nghiệm x1, x2, tạo thành ba khoảng xét dấu. Nếu a > 0, dấu dương nằm ngoài hai nghiệm và dấu âm nằm giữa hai nghiệm. Nếu a < 0, dấu âm nằm ngoài và dấu dương nằm giữa.
- Trường hợp Δ = 0, dấu của f(x) không đổi trên toàn bộ trục số thực và cùng dấu với hệ số a, ngoại trừ tại nghiệm kép.
- Khi Δ < 0, tam thức không có nghiệm thực, và dấu của f(x) luôn trùng với dấu của a.

Phương pháp ứng dụng dấu của tam thức bậc hai
Trong toán học, các bài tập về dấu của tam thức bậc hai là công cụ hiệu quả để giải quyết nhiều dạng toán, đặc biệt là các bài toán liên quan đến bất phương trình bậc hai. Dưới đây là một số nhận định quan trọng:
- Nếu Δ > 0, toán 10 dấu của tam thức bậc hai sẽ có cả dấu dương và âm trên trục số thực.
- Nếu Δ ≤ 0, tam thức chỉ mang một dấu duy nhất (luôn dương hoặc luôn âm).
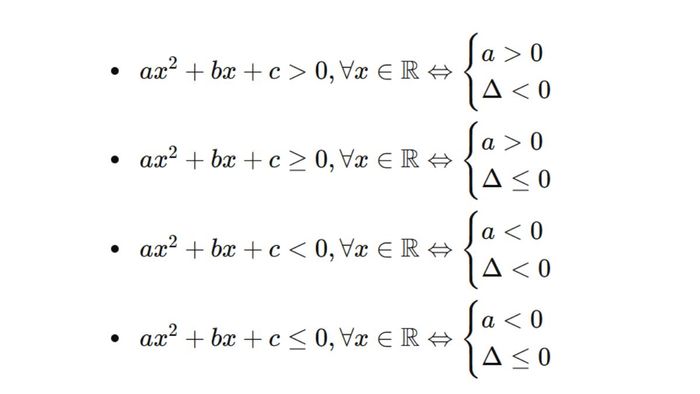
Bảng xét dấu là một công cụ hữu ích giúp xác định các khoảng giá trị của biến số thỏa mãn điều kiện đã cho.
Hàm số:
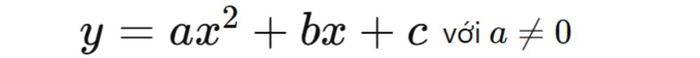
Hàm số có thể đồng biến hoặc nghịch biến trên từng khoảng được xác định bởi các nghiệm.
Tính toán các đại lượng như thời gian, khoảng cách, vận tốc trong các bài toán vật lý hoặc tối ưu hóa.

Tổng hợp các bài tập thực hành về dấu của tam thức bậc hai
Sau khi hiểu rõ lý thuyết về dấu của tam thức bậc hai và phương pháp xét dấu, các bài tập vận dụng sẽ giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán. Dưới đây là một số bài tập về dấu của tam thức bậc hai giúp bạn áp dụng hiệu quả những nguyên tắc đã học vào thực tiễn.
Câu 1: Biểu thức nào sau đây được xem là tam thức bậc hai?
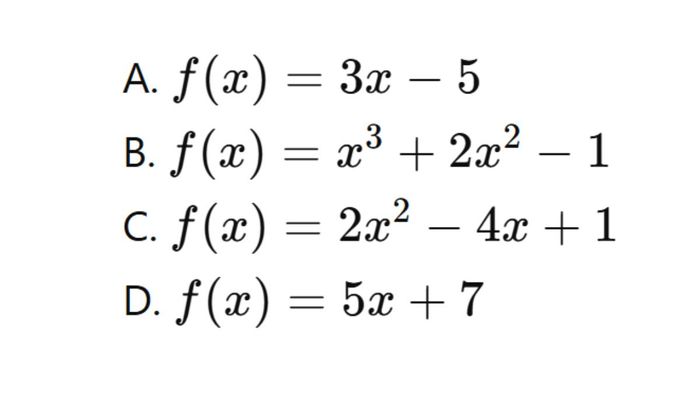
Đáp án đúng: C
Đáp án A và D là các nhị thức bậc nhất.
Đáp án B là một đa thức bậc ba.
Đáp án C là tam thức bậc hai do có dạng phù hợp.

Câu 2: Xác định điều kiện của m
- m < 3
- m > 3
- m ≥ 3
- m ≤ 3
Đáp án đúng: B
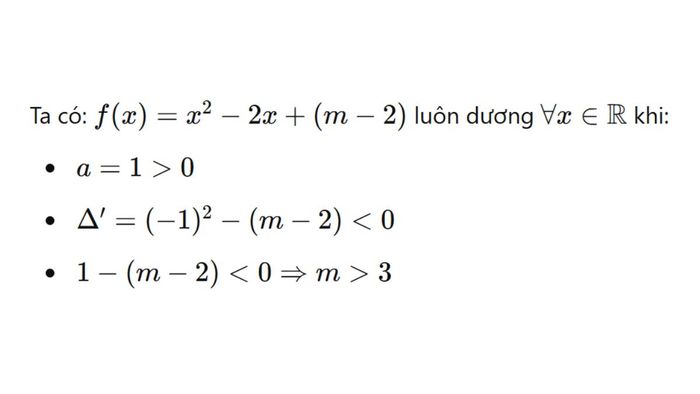
Câu 3: Tìm tập nghiệm của bất phương trình
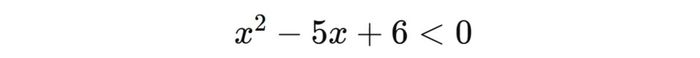

Nắm vững dấu của tam thức bậc hai giúp bạn phân tích chính xác các biểu thức, từ đó dễ dàng giải quyết các bài toán về bất phương trình và khoảng giá trị của hàm số. Hy vọng bài viết này đã giúp bạn hiểu rõ phương pháp xét dấu và áp dụng linh hoạt vào thực tế. Hãy tiếp tục khám phá thêm nhiều công thức toán học hữu ích tại Mytour!
