Nắm vững công thức tính diện tích parabol không chỉ giúp giải quyết các bài toán tính toán mà còn hỗ trợ xử lý dữ liệu trong nhiều ngành nghề khác nhau. Vì vậy, Mytour sẽ đồng hành cùng bạn khám phá khái niệm cũng như cách xác định diện tích hình parabol. Đồng thời, các bài tập thực hành sẽ giúp bạn tiếp thu kiến thức một cách hiệu quả và dễ dàng.
Định nghĩa về diện tích parabol
Đây là vùng không gian được xác định bởi đường cong parabol và một đoạn thẳng trên trục hoành hoặc một đường giới hạn khác. Trong toán học, việc tính toán diện tích parabol đóng vai trò quan trọng trong các bài toán ứng dụng liên quan đến hình học giải tích, kỹ thuật và vật lý.
Parabol là một đường cong bậc hai có phương trình tổng quát dạng:
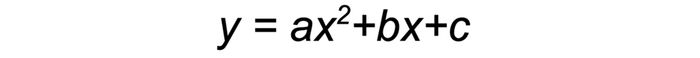
Khi tính toán diện tích hình parabol, chúng ta thường xem xét vùng không gian được giới hạn bởi đường parabol và trục hoành trong một khoảng xác định. Quá trình tính toán này không thể áp dụng các công thức đơn giản như với hình tam giác hay hình chữ nhật, mà cần sử dụng phương pháp tích phân để xác định chính xác.

Để học tập hiệu quả và tiếp thu kiến thức một cách thông minh, một chiếc máy đọc sách đi kèm bút cảm ứng sẽ là công cụ hỗ trợ đắc lực. Với màn hình chống mỏi mắt và khả năng ghi chú tiện lợi, thiết bị này giúp bạn đọc tài liệu và làm bài tập ứng dụng mọi lúc, mọi nơi. Hãy tham khảo ngay và trang bị cho mình một chiếc máy đọc sách để nâng cao hiệu suất học tập và tiếp thu kiến thức một cách khoa học hơn:
Phương pháp tính diện tích parabol
Để xác định diện tích parabol, chúng ta cần áp dụng phép tính tích phân. Công thức tính diện tích parabol thường được biểu diễn như sau:

Ví dụ, xét đường parabol có phương trình y=x2 trong khoảng [0,2], diện tích parabol được tính toán theo công thức sau:
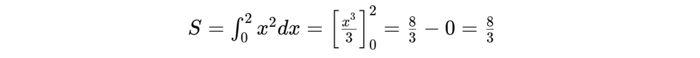
Bên cạnh việc sử dụng tích phân, trong một số trường hợp đơn giản, người ta có thể áp dụng công thức tính diện tích parabol dựa trên tính đối xứng của hình dạng. Tuy nhiên, phương pháp tích phân vẫn là cách chính xác và được sử dụng rộng rãi nhất.

Bài tập thực hành tính diện tích parabol
Sau khi nắm vững khái niệm diện tích hình parabol và công thức tính toán, việc thực hành qua các bài tập cụ thể sẽ giúp bạn áp dụng kiến thức một cách hiệu quả. Thông qua các bài toán thực tế, bạn sẽ rèn luyện kỹ năng tính toán, làm quen với nhiều dạng bài đa dạng và nâng cao khả năng giải quyết vấn đề một cách logic.

Dưới đây là một số bài tập tính diện tích parabol kèm lời giải chi tiết, giúp bạn dễ dàng hiểu rõ phương pháp tính toán và tránh những lỗi thường gặp.


Giải đáp các thắc mắc liên quan đến diện tích parabol
Việc tính toán diện tích parabol giúp xác định kích thước của vùng không gian được giới hạn bởi đường cong này, từ đó áp dụng vào các bài toán hình học, kỹ thuật và khoa học. Để hiểu sâu hơn về tầm quan trọng của diện tích hình parabol, hãy cùng khám phá lý do tại sao công thức tính toán này lại cần thiết.
Tại sao cần tính diện tích hình parabol?
Công thức tính diện tích parabol hiện nay được ứng dụng rộng rãi trong nhiều lĩnh vực thực tiễn, phục vụ cho các công trình kỹ thuật quan trọng. Dưới đây là một số lý do chính khiến việc tính diện tích hình parabol trở nên thiết yếu:
- Giải quyết các bài toán hình học và tính toán diện tích vùng cong
Khi giải quyết các bài toán liên quan đến hình học không gian hoặc hình học phẳng, công thức tính diện tích parabol giúp xác định vùng không gian được giới hạn bởi parabol và trục tọa độ. Công thức này đóng vai trò quan trọng trong việc tính toán các đường cong vòng cung thông qua phương pháp tích phân.
- Ứng dụng trong lĩnh vực kỹ thuật và thiết kế công trình xây dựng
Trong lĩnh vực xây dựng, nhiều công trình có mái vòm hoặc kiến trúc dạng vòng cung, vì vậy việc tính diện tích hình parabol giúp tối ưu hóa thiết kế và dự toán nguyên vật liệu. Trong ngành cơ khí, các tấm chắn parabol được sử dụng để tối ưu hóa thiết bị phản xạ sóng như ăng-ten và kính thiên văn.

- Hỗ trợ mô phỏng và tính toán trong lĩnh vực vật lý và thiên văn học
Trong vật lý, đặc biệt là quang học và động lực học, parabol được sử dụng để mô phỏng quỹ đạo của vật thể hoặc hệ thống phản xạ ánh sáng. Trong thiên văn học, các kính viễn vọng parabol giúp thu thập ánh sáng từ các thiên thể ở xa.
Diện tích parabol được ứng dụng thực tế như thế nào?
Không chỉ dừng lại ở lý thuyết, công thức tính diện tích parabol còn có nhiều ứng dụng quan trọng trong đời sống. Dưới đây là một số lĩnh vực nổi bật mà công thức này được áp dụng:
- Trong ngành xây dựng và kiến trúc
Các công trình như cầu vòm, mái che, nhà hát thường sử dụng thiết kế parabol để tăng tính thẩm mỹ và khả năng chịu lực. Việc tính diện tích hình parabol giúp xác định diện tích bề mặt, từ đó tối ưu hóa chi phí nguyên vật liệu, đặc biệt trong các dự án có quy mô lớn.
- Trong lĩnh vực viễn thông và quang học
Ăng-ten parabol giúp thu và khuếch đại tín hiệu hiệu quả, từ truyền hình vệ tinh đến mạng không dây. Các kính thiên văn parabol hỗ trợ thu nhận ánh sáng từ không gian với độ chính xác cao, phục vụ nghiên cứu vũ trụ.
- Trong ngành cơ khí và giao thông vận tải
Một số bộ phận của xe ô tô, đặc biệt là đèn pha, được thiết kế theo hình parabol để tập trung ánh sáng hiệu quả hơn. Đường băng sân bay cũng áp dụng hình dạng parabol để tối ưu hóa góc tiếp đất của máy bay, đảm bảo an toàn khi hạ cánh.
Nắm vững công thức tính diện tích parabol sẽ giúp bạn giải quyết hiệu quả các bài toán hình học và ứng dụng thực tiễn. Dù trong học tập hay các ngành như kiến trúc, kỹ thuật, kỹ năng tính toán này đều mang lại giá trị thiết thực. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về diện tích hình parabol và có thể áp dụng linh hoạt vào nhiều tình huống khác nhau.
