Việc chứng minh định lý Pitago là một phần thiết yếu trong chương trình toán, giúp học sinh hiểu rõ mối liên hệ giữa ba cạnh của tam giác vuông. Ngoài ra, định lý Pitago đảo còn là công cụ hữu ích để xác định một tam giác có phải là tam giác vuông hay không. Nắm vững hai định lý này sẽ hỗ trợ bạn hiệu quả trong giải toán hình học và ứng dụng thực tiễn như đo đạc, xây dựng và kỹ thuật.
Tìm hiểu về Định lý Pitago và định lý đảo của nó
Cả định lý Pitago (thuận) lẫn định lý Pitago đảo đều rất quan trọng trong việc xác định tính chất của một tam giác. Khi hiểu sâu hai định lý này, bạn có thể áp dụng hiệu quả vào các bài toán hình học cũng như trong thực tế như đo đạc, xây dựng và tính toán khoảng cách.
Định lý Pitago cơ bản
Định lý Pitago nêu rõ: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Định lý này có nhiều ứng dụng thực tiễn trong toán học và đời sống, như tính khoảng cách trên mặt phẳng hay trong không gian, kiểm tra độ chính xác của công trình xây dựng hoặc xác định tọa độ vị trí.

Việc học toán sẽ trở nên hiệu quả hơn nếu bạn sử dụng một chiếc máy đọc sách đi kèm bút cảm ứng. Thiết bị này giúp bạn dễ dàng ghi chú, lưu trữ tài liệu và theo dõi bài giảng trực quan. Tham khảo các mẫu máy sở hữu màn hình chống chói và dung lượng lớn dưới đây để nâng cao hiệu suất học tập của mình nhé!
Khái quát về định lý Pitago đảo
Định lý Pitago đảo được phát biểu như sau: Nếu tổng bình phương hai cạnh ngắn hơn bằng bình phương cạnh dài nhất thì tam giác đó là tam giác vuông. Nói cách khác, trong tam giác vuông, ba cạnh sẽ thỏa mãn công thức sau đây:
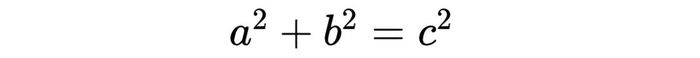
Định lý Pitago đảo là công cụ hữu ích để xác định một tam giác có vuông hay không, hỗ trợ kiểm tra chính xác trong quá trình đo đạc và thiết kế.
Công thức định lý Pitago
Định lý Pitago là một trong những định lý cơ bản và quan trọng nhất của hình học Euclid, mang tên nhà toán học Hy Lạp cổ đại Pythagoras. Định lý này chỉ ra mối liên hệ giữa ba cạnh trong một tam giác vuông.
Cụ thể, trong tam giác vuông, bình phương cạnh huyền (là cạnh đối diện góc vuông) bằng tổng bình phương hai cạnh góc vuông còn lại. Công thức Pitago được trình bày như sau:

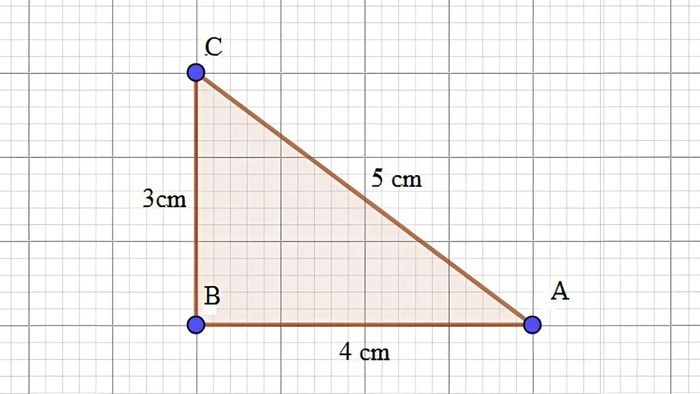
Phương pháp chứng minh định lý Pitago
Có nhiều phương pháp khác nhau để chứng minh định lý Pitago trong hình học, nhưng cách phổ biến và dễ hiểu nhất là sử dụng diện tích. Xét một hình vuông có cạnh dài a+b, chứa bốn tam giác vuông với các cạnh a, b, c. Diện tích hình vuông này có thể được tính theo hai cách khác nhau:
- Tổng diện tích của bốn tam giác vuông và hình vuông nhỏ nằm giữa:
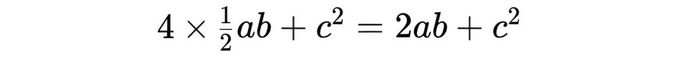
- Diện tích của toàn bộ hình vuông lớn:
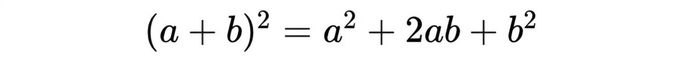
Khi so sánh hai kết quả, ta thu được:
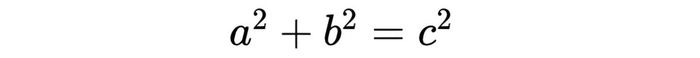
Đây chính là công thức của định lý Pitago, và ví dụ minh họa bên dưới sẽ giúp bạn hiểu rõ hơn về cách áp dụng:


Bài tập áp dụng định lý Pitago trong chương trình Toán lớp 7
Để vận dụng thành thạo định lý Pitago, học sinh nên luyện tập qua nhiều dạng bài. Dưới đây là một số bài toán giúp củng cố khả năng sử dụng công thức Pitago để giải quyết các bài toán thực tế.
Bài 1: Cho một tam giác vuông, biết hai cạnh góc vuông lần lượt dài 6 cm và 8 cm.
Bài 2: Một chiếc thang đặt nghiêng vào tường, điểm tựa trên cao cách mặt đất 2m. Biết chiều dài thang là 2.5m, tính khoảng cách từ chân thang đến chân tường.
Bài 3: Một mảnh đất hình chữ nhật có chiều dài 9m và chiều rộng 12m. Hãy tính độ dài đường chéo của mảnh đất đó.

Những điều cần chú ý khi học định lý Pitago
Trong quá trình học định lý Pitago, học sinh cần nắm rõ một số điểm then chốt để vận dụng chính xác công thức, tránh mắc lỗi khi giải bài. Việc hiểu kỹ bản chất định lý, nắm vững nguyên tắc áp dụng sẽ giúp học tốt hơn và hiệu quả hơn:
- Xác định đúng tam giác vuông: Chỉ áp dụng định lý Pitago cho tam giác vuông nên phải xác định đúng góc vuông.
- Áp dụng chính xác công thức: Sử dụng đúng công thức Pitago và biến đổi linh hoạt để giải bài toán.
- Hỗ trợ bằng hình vẽ: Vẽ hình minh họa giúp dễ hình dung và vận dụng định lý một cách trực quan.

Việc nắm vững định lý Pitago và hiểu cách chứng minh sẽ giúp bạn dễ dàng ứng dụng trong các dạng toán khác nhau cũng như trong thực tế. Đồng thời, biết cách sử dụng định lý Pitago đảo sẽ hỗ trợ bạn kiểm tra nhanh xem một tam giác có vuông hay không. Hãy kiên trì luyện tập để nâng cao trình độ toán học của bạn!
