Định lý Pytago lớp 8 là một trong những kiến thức trọng tâm mà học sinh cần nắm vững. Việc hiểu rõ công thức của định lý Pytago sẽ giúp bạn giải quyết các bài toán nhanh chóng và hiệu quả hơn. Cùng khám phá các công thức và ứng dụng của định lý này qua bài viết dưới đây.
Định lý Pytago có ý nghĩa gì?
Định lý Pytago là một trong những công thức cơ bản và nổi bật trong toán học, xác định mối quan hệ giữa ba cạnh của tam giác vuông. Theo đó, bình phương cạnh huyền luôn bằng tổng bình phương của hai cạnh góc vuông. Đây là cơ sở cho nhiều ứng dụng trong hình học và các lĩnh vực khác nhau.
Việc hiểu rõ định lý này không chỉ giúp bạn giải quyết các bài toán một cách hiệu quả mà còn phát triển khả năng tư duy logic. Ngoài ra, định lý Pytago lớp 8 được ứng dụng rộng rãi trong các bài toán thực tế, giúp nâng cao hiệu quả công việc. Đây cũng là nền tảng quan trọng trong các nghiên cứu hình học và toán học nâng cao sau này.

Laptop là công cụ tuyệt vời giúp học sinh giải quyết các bài toán, đặc biệt là các bài tập về định lý Pytago. Với khả năng tính toán chính xác và nhanh chóng, laptop hỗ trợ học sinh xử lý các bài tập hình học phức tạp một cách dễ dàng. Cùng tham khảo các mẫu laptop bên dưới để nâng cao hiệu quả học tập của bạn!
Công thức của định lý Pytago là gì?
Định lý Pytago là nền tảng quan trọng trong hình học, mở ra nhiều ứng dụng phong phú trong các lĩnh vực khác nhau. Nội dung này sẽ giúp bạn hiểu rõ hơn về công thức của định lý Pytago đảo và cách giải các bài tập liên quan đến định lý này.
Định lý Pytago là gì?
Công thức của định lý Pytago là mối quan hệ vô cùng quan trọng trong hình học. Nó cho phép tính toán chiều dài của các cạnh trong tam giác vuông dựa trên hai cạnh còn lại. Định lý này cũng là cơ sở để giải quyết vô số bài toán hình học phức tạp.
Công thức toán học của định lý Pytago là gì?
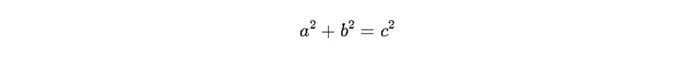
Trong đó:
- a và b là độ dài của hai cạnh vuông góc của tam giác
- c là chiều dài của cạnh huyền (cạnh đối diện góc vuông)
Định lý Pytago đảo là gì?
Định lý Pytago không chỉ có công thức chuẩn mà còn có thể đảo ngược. Định lý này nói rằng: Nếu trong một tam giác, bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại, thì tam giác đó chắc chắn là tam giác vuông. Công thức của định lý Pytago đảo được trình bày như sau:

Định lý Pytago đảo là công cụ hữu ích để nhận diện tam giác vuông chỉ thông qua các cạnh của nó. Công thức này mở rộng khả năng ứng dụng của định lý Pytago trong các tình huống toán học khác nhau.
Cách chứng minh định lý Pytago một cách đơn giản nhất
Một trong những phương pháp trực quan và dễ hiểu nhất để chứng minh định lý Pytago là sử dụng hình học. Bạn có thể vẽ một hình vuông với cạnh là tổng của các cạnh vuông trong tam giác vuông. Sau đó, chia hình vuông lớn thành các phần nhỏ có diện tích tương ứng với tổng diện tích của các hình vuông nhỏ từ các cạnh của tam giác vuông.
Kết quả là, tổng diện tích của các hình vuông nhỏ sẽ bằng diện tích của hình vuông lớn. Phương pháp này mang đến một hình ảnh sinh động, giúp bạn hiểu rõ hơn về sự liên kết kỳ diệu giữa các cạnh trong tam giác vuông. Cách chứng minh này cũng giúp bạn tiếp cận định lý Pytago lớp 8 một cách dễ dàng và trực quan.
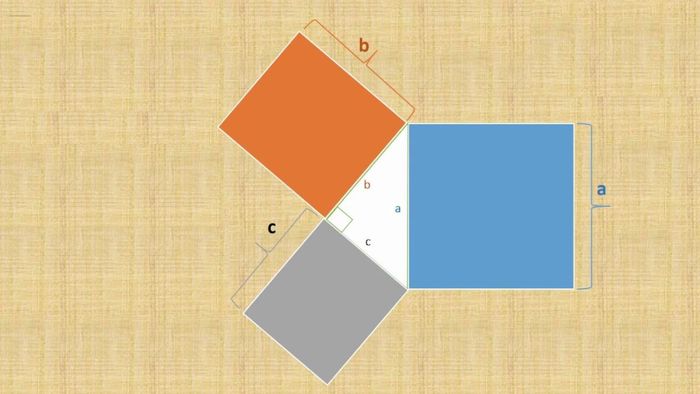
Bài tập áp dụng định lý Pytago
Các bài tập ứng dụng định lý Pytago hoặc công thức định lý Pytago đảo rất đa dạng và phong phú. Người học có thể bắt đầu với các bài toán tính cạnh huyền, rồi sau đó chuyển sang các bài toán thực tế như tính khoảng cách giữa hai điểm trên mặt phẳng. Những bài tập này giúp củng cố kiến thức và phát triển kỹ năng giải quyết vấn đề. Việc luyện tập đều đặn giúp người học sử dụng định lý này một cách hiệu quả hơn.
Dưới đây là một số bài tập ứng dụng định lý Pytago lớp 8 để bạn tham khảo và củng cố kiến thức:
Bài tập 1: Cho một tam giác vuông có hai cạnh vuông góc lần lượt là 6 cm và 8 cm. Hãy tính độ dài của cạnh huyền.
Giải: Áp dụng công thức của định lý Pytago

Bài tập 2: Cho tam giác ABC với góc vuông tại A. Biết rằng AB = 7 cm và AC = 24 cm. Tính độ dài của cạnh BC.
Giải: Sử dụng công thức của định lý Pytago

Giải quyết các bài tập này không chỉ giúp bạn làm quen với lý thuyết mà còn rèn luyện khả năng tư duy logic. Tiếp tục thực hành và tìm hiểu thêm nhiều bài tập để củng cố và nâng cao kiến thức của mình.
Bằng việc tìm hiểu và ứng dụng công thức định lý Pytago đảo, bạn đã nắm vững một kiến thức quan trọng. Đây là nền tảng vững chắc, không chỉ trong học tập mà còn ứng dụng mạnh mẽ trong thực tế. Với kiến thức định lý Pytago lớp 8, bạn sẽ tự tin đối diện với những thử thách toán học khó khăn phía trước.
