Định lý Viet và các ứng dụng, bài tập liên quan

Có gặp khó khăn với các phương trình bậc hai phức tạp? Định lý Viet sẽ giúp bạn giải quyết chúng nhanh chóng và hiệu quả. Không chỉ hỗ trợ giải phương trình, định lý này còn mở rộng ra nhiều ứng dụng hữu ích trong các lĩnh vực toán học khác. Cùng Mytour tìm hiểu kỹ hơn về định lý Viet, từ đảo, lớp 9, tổng quát, bậc 2, bậc 3 và cách áp dụng vào thực tiễn nhé.

Khám phá định lý Viet

Định lý Viet là một hệ thức quan trọng trong toán học, đặc biệt hữu ích trong việc giải các bài toán phương trình bậc hai. Được phát triển bởi nhà toán học người Pháp François Viet, định lý này không chỉ giúp tìm ra mối quan hệ giữa các nghiệm của phương trình mà còn mở rộng nhiều ứng dụng trong các lĩnh vực khác như đại số và lý thuyết số. Hãy cùng tìm hiểu chi tiết về định lý Viet, cách áp dụng vào bài toán thực tế và những ví dụ cụ thể để nắm vững lý thuyết này.

Định lý thuận

Định lý Viet là một công cụ không thể thiếu trong việc giải quyết các bài toán phương trình bậc hai. Công thức này cho phép xác định mối quan hệ giữa các nghiệm và các hệ số của phương trình, từ đó rút ra những kết luận quan trọng và hữu ích. Định lý Viet thuận có rất nhiều ứng dụng, từ việc giải phương trình một cách nhanh chóng cho đến việc xây dựng phương trình mới dựa trên các điều kiện đã cho.

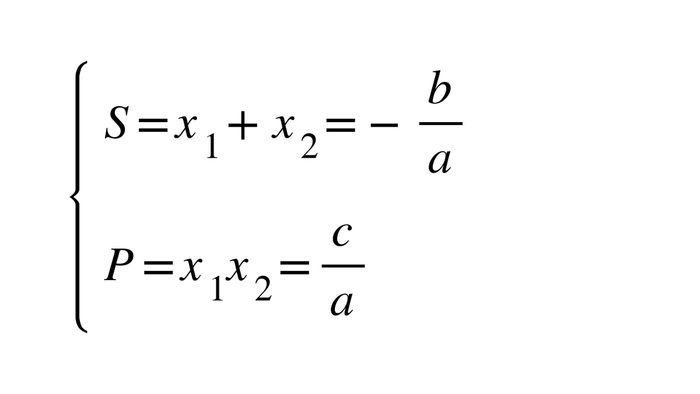
Định lý Viet đảo

Đây là một công cụ quan trọng trong toán học, giúp chúng ta tạo ra phương trình bậc hai khi biết tổng và tích của các nghiệm. Định lý đảo, trái ngược với định lý Viet thuận, cho phép chúng ta xây dựng phương trình từ những kết quả đã có. Đây là một mối quan hệ quan trọng, mở rộng khả năng giải quyết các bài toán liên quan đến phương trình bậc hai.

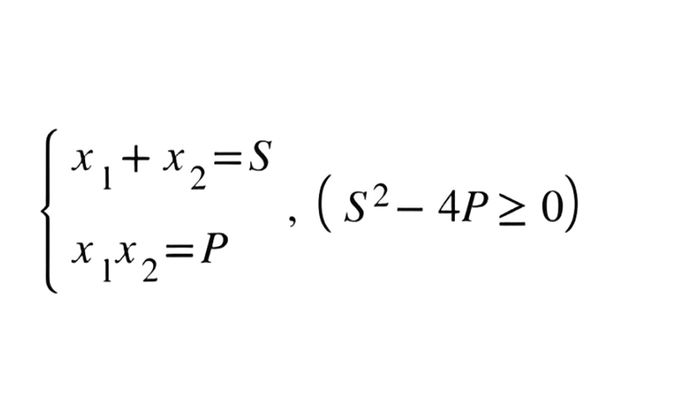
Ứng dụng của định lý Viet

Định lý Viet không chỉ có giá trị trong việc giải các bài toán lý thuyết mà còn được áp dụng rộng rãi trong nhiều lĩnh vực như điện tử, kỹ thuật và kinh tế. Khi cần giải quyết các bài toán tối ưu hóa hoặc mô hình hóa những quá trình phức tạp, định lý Viet mang đến những phương pháp đơn giản và hiệu quả cho nhiều tình huống thực tế.

Định lý Viet đối với các bậc phương trình

Định lý Viet không chỉ có ứng dụng đối với phương trình bậc hai mà còn phát huy hiệu quả trong việc giải các phương trình bậc cao hơn. Từ việc tính tổng và tích nghiệm cho đến phân tích đồ thị, định lý này mang đến nhiều ứng dụng hữu ích cho cả toán học lý thuyết lẫn thực tế. Cùng tìm hiểu vai trò của định lý Viet trong việc giải quyết các phương trình ở các bậc khác nhau.

Định lý Viet bậc 2

Định lý Viet bậc 2 là công cụ quan trọng để giải quyết các bài toán phương trình bậc 2, đặc biệt khi tìm nghiệm cho phương trình có dạng ax² + bx + c = 0 (với a ≠ 0). Nếu hai nghiệm của phương trình là x₁ và x₂, ta có các hệ thức liên quan giữa nghiệm và hệ số.

Định lý Viet bậc 2 giúp tính toán nhanh chóng nghiệm của phương trình, kiểm tra đáp án và phân tích bài toán một cách chính xác. Đây là một kiến thức nền tảng quan trọng trong các kỳ thi và các ứng dụng trong thực tế.

Định lý Viet bậc 3

Định lý Viet bậc 3 cung cấp công cụ mạnh mẽ để xác định mối quan hệ giữa nghiệm và hệ số trong phương trình bậc 3. Với phương trình có dạng ax³ + bx² + cx + d = 0, nếu phương trình có ba nghiệm x₁, x₂, x₃, định lý này sẽ giúp bạn nhanh chóng tính toán các hệ số từ các nghiệm đó.

Định lý Viet bậc 3 là công cụ đắc lực trong giải toán đại số, giúp nhanh chóng tìm nghiệm và phân tích các bài toán về đồ thị của các hàm bậc ba. Áp dụng định lý này không chỉ giúp tiết kiệm thời gian mà còn tăng độ chính xác trong việc giải phương trình.

Định lý Viet cho các phương trình đa thức tổng quát

Đối với phương trình đa thức bậc n có cấu trúc như sau:

P(x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀ = 0

Giả sử phương trình có các nghiệm là x₁, x₂, ..., x_n, ta có công thức sau đây:

Các công thức tương tự cũng áp dụng cho tổng các tích bậc cao của nghiệm. Định lý Viet là một công cụ mạnh mẽ giúp giải các phương trình đa thức và tìm nghiệm mà không cần phải giải chi tiết từng bước.

Các ứng dụng thiết thực của định lý Viet

Định lý Viet tổng quát không chỉ là một lý thuyết toán học quan trọng mà còn có rất nhiều ứng dụng thực tế có giá trị. Dưới đây là một số ví dụ điển hình được áp dụng trong các bài toán tổng quát:

• Tính tổng và tích các nghiệm một cách trực tiếp từ các hệ số của phương trình.
• Giải quyết các bài toán trong các lĩnh vực như chuyển động, vật lý, và kinh tế có liên quan đến phương trình bậc hai.
• Xác định nhanh chóng nghiệm của phương trình mà không cần phải giải chi tiết từng bước.
• Áp dụng tổng và tích nghiệm để phân tích tính chất đồ thị của hàm số bậc hai.

Một số bài tập ứng dụng

Dưới đây là một số bài tập minh họa cách ứng dụng định lý Viet mà bạn có thể tham khảo:

Bài tập 1: Tìm hai nghiệm của phương trình bậc hai khi biết tổng và tích

Đề bài: Tìm phương trình bậc hai khi tổng nghiệm x₁ + x₂ = 5 và tích nghiệm x₁ . x₂ = 6.

Bài tập 2: Chứng minh một mối quan hệ giữa các nghiệm

Đề bài: Ta có bài toán như sau:

Bài tập 3: Xác định điều kiện của nghiệm

Đề bài: Cho phương trình x₁ - px + q = 0. Xác định điều kiện của p, q để hai nghiệm x₁ , x₂ thỏa mãn x₁ > 0 và x₂ > 0

Định lý Viet không chỉ giúp giải các phương trình bậc hai hiệu quả mà còn cung cấp nhiều ứng dụng quan trọng trong đại số. Việc nắm vững định lý Viet, từ cơ bản đến nâng cao, sẽ giúp bạn tiết kiệm thời gian giải quyết bài toán và phát triển khả năng tư duy logic cũng như kỹ năng giải toán. Những bài tập và ví dụ thực tế sẽ giúp bạn hiểu sâu hơn và áp dụng tốt hơn trong học tập và thi cử.

• Khám phá các kiến thức mới nhất về Toán học tại các chuyên mục: Giáo dục và Góc Học & Day 4.0