Khi nghiên cứu hình học phẳng, nhiều người bắt đầu băn khoăn về tính chất và công thức của đường trung tuyến trong tam giác. Nắm vững kiến thức về đường trung tuyến trong các loại tam giác vuông, đều, cân sẽ giúp bạn dễ dàng giải quyết những bài toán khó. Đọc bài viết này trên Mytour để hiểu thêm nhé!
Khái niệm đường trung tuyến là gì?
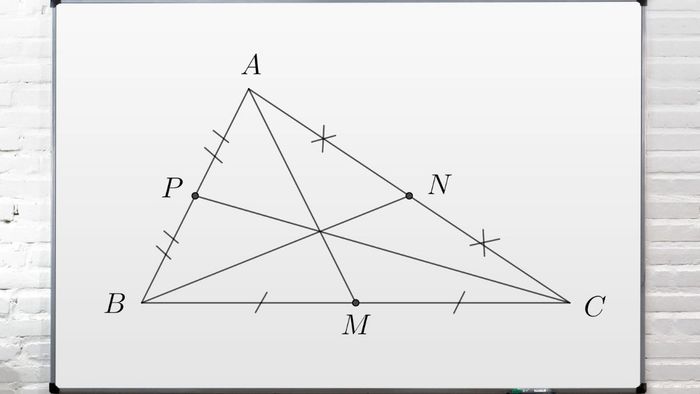
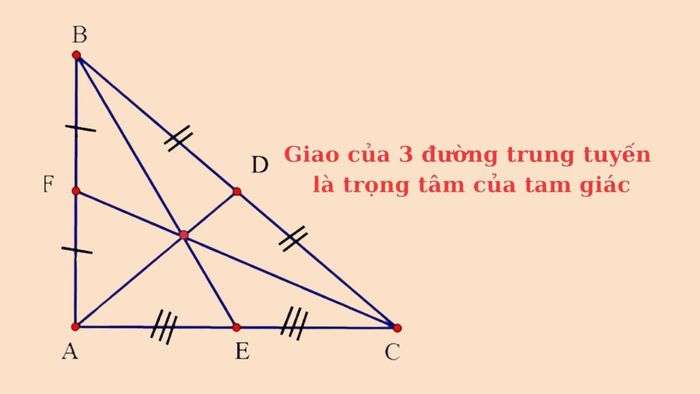
Trong hình học phẳng, đường trung tuyến là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Điểm gặp nhau của ba đường trung tuyến trong tam giác chính là trọng tâm của nó.
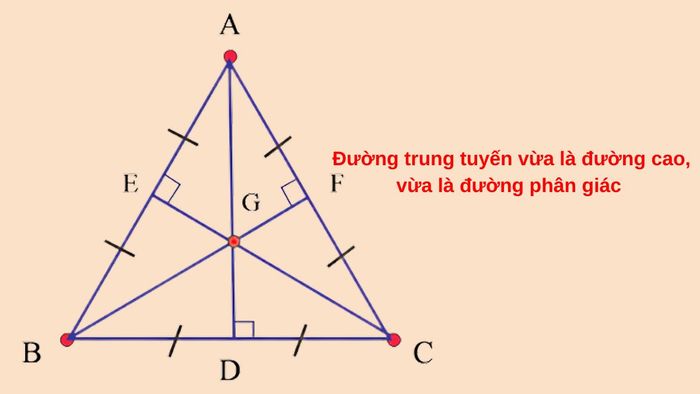
Với tam giác cân, đường trung tuyến xuất phát từ đỉnh của góc cân không chỉ chia đôi cạnh đáy mà còn là phân giác của góc tại đỉnh. Còn trong tam giác đều, ba đường trung tuyến đồng thời là đường phân giác, đường cao và đường trung trực.
Trong không gian ba chiều, khái niệm về đường trung tuyến được mở rộng thành mặt phẳng trung tuyến trong tứ diện. Mặt phẳng này đi qua trung điểm của một cạnh và có thể song song hoặc vuông góc với các mặt chứa các cạnh tương ứng.
Trong quá trình học tập, laptop là công cụ không thể thiếu giúp bạn học hiệu quả. Hãy tham khảo các mẫu laptop đang hot nhất tại Mytour để nhận giá ưu đãi cùng bảo hành uy tín.
Những tính chất quan trọng của đường trung tuyến
Đường trung tuyến trong tam giác là một khái niệm quan trọng trong hình học phẳng. Việc nắm vững tính chất của đường trung tuyến giúp bạn áp dụng hiệu quả vào việc giải các bài toán hình học hoặc chứng minh các định lý liên quan đến tam giác.
Đường trung tuyến trong tam giác vuông
Tam giác vuông có một góc vuông (90°) và hai cạnh tạo thành góc vuông vuông góc với nhau. Một tính chất đặc biệt của đường trung tuyến trong tam giác vuông là đường trung tuyến từ đỉnh góc vuông đến trung điểm của cạnh huyền đối diện sẽ có độ dài bằng một nửa cạnh huyền.
Nếu một tam giác có đường trung tuyến bằng nửa chiều dài của một cạnh, đó chính là tam giác vuông. Nó vẫn giữ nguyên các đặc điểm cơ bản của đường trung tuyến, bao gồm việc chia tam giác thành các phần có diện tích bằng nhau.
Đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh và kéo dài đến trung điểm của cạnh đáy, tạo thành một góc vuông 90 độ với cạnh đáy. Tính chất này chia tam giác thành hai tam giác vuông đồng dạng, có diện tích bằng nhau. Đồng thời, đường này cũng là đường phân giác và đường cao, đảm bảo sự đối xứng tuyệt đối trong tam giác cân.
Đường trung tuyến trong tam giác đều
Trong tam giác đều, ba đường trung tuyến cắt nhau tại trọng tâm, chia tam giác thành sáu phần nhỏ có diện tích đều nhau. Mỗi đường trung tuyến đồng thời là đường cao và phân giác, tạo ra sự đối xứng hoàn hảo. Khi vẽ một đường thẳng từ bất kỳ đỉnh nào đi qua trọng tâm, nó sẽ chia tam giác thành hai phần có diện tích bằng nhau.
Ba định lý quan trọng về đường trung tuyến trong tam giác
Để hiểu rõ hơn về các tính chất và đặc điểm của đường trung tuyến trong tam giác, chúng ta cần tìm hiểu ba định lý cơ bản. Các định lý này giúp làm rõ mối quan hệ giữa các đường trung tuyến và trọng tâm, đồng thời chỉ ra cách chúng phân chia diện tích của tam giác. Ba định lý quan trọng mà bạn cần ghi nhớ bao gồm:
Định lý 1: Điểm giao của ba đường trung tuyến trong tam giác chính là trọng tâm của tam giác.
Định lý 2: Ba đường trung tuyến chia tam giác thành sáu phần nhỏ có diện tích bằng nhau, và mỗi đường trung tuyến sẽ chia tam giác thành hai phần có diện tích giống nhau.
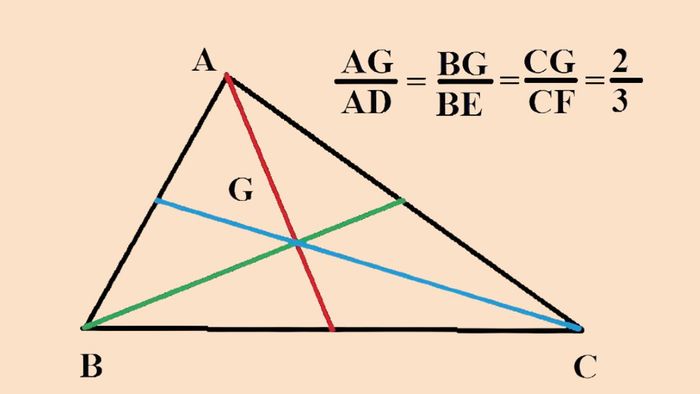
Định lý 3: Khoảng cách từ trọng tâm đến đỉnh của tam giác bằng ⅔ chiều dài của đường trung tuyến xuất phát từ đỉnh đó.
Công thức tính chiều dài đường trung tuyến trong tam giác
Dưới đây là công thức tính đường trung tuyến, ví dụ với tam giác ABC có đường trung tuyến xuất phát từ đỉnh A đến trung điểm của cạnh BC:
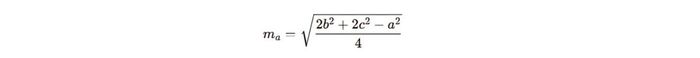
Trong công thức này:
a, b, c là các cạnh của tam giác.
m là độ dài của đường trung tuyến trong tam giác
Tương tự, công thức này có thể được sử dụng để tính đường trung tuyến tại các đỉnh B và C của tam giác, dựa trên định lý cosin, giúp tính chính xác độ dài đường trung tuyến trong mọi loại tam giác.
- Tham khảo thêm các bài viết tại chuyên mục: Giáo dục; Góc Học & Dạy 4.0.
Một số bài tập ứng dụng
Bài tập 1: Cho tam giác vuông ABC với ∠ABC = 90 độ, các cạnh có độ dài lần lượt là a = 6, b = 8 và c = 10 (với c là cạnh huyền). Hãy tính chiều dài của đường trung tuyến từ đỉnh A.
Lời giải:
Vì tam giác ACB vuông, ta áp dụng đặc điểm riêng của tam giác vuông, theo đó độ dài của đường trung tuyến từ đỉnh A đến trung điểm cạnh huyền sẽ bằng ½ chiều dài cạnh huyền BC.
Vậy độ dài của đường trung tuyến m là: m = c/2 = 10/2 = 5
Bài tập 2: Tam giác ABC có các cạnh lần lượt là a = 7, b = 9 và c = 10. Hãy tính độ dài của đường trung tuyến từ đỉnh A.

Bài tập 3: Tam giác ABC là tam giác đều với cạnh a = 10. Tính độ dài của đường trung tuyến.

Chúng ta đã cùng tìm hiểu về tính chất và công thức của đường trung tuyến, cũng như các đặc điểm quan trọng của nó. Việc hiểu rõ đường trung tuyến trong tam giác vuông, đều và cân sẽ giúp bạn giải quyết các bài toán một cách linh hoạt. Hy vọng những kiến thức này sẽ hỗ trợ bạn khi làm các bài toán hình học liên quan.
