Tính chất hình thoi là gì? Đây là câu hỏi phổ biến khi bắt đầu tìm hiểu về loại tứ giác đặc biệt này. Hình thoi có bốn cạnh đều nhau, các đường chéo cắt nhau vuông góc, mang lại nhiều tính chất thú vị cả trong lý thuyết lẫn ứng dụng thực tế. Bài viết này sẽ giới thiệu về khái niệm, cách tính diện tích và những bài tập áp dụng thực tế của hình thoi.
Hình thoi là một tứ giác có bốn cạnh bằng nhau
Hình thoi là tứ giác có bốn cạnh đều, là một dạng đặc biệt của hình bình hành. Mặc dù mọi hình thoi đều là hình bình hành, nhưng không phải tất cả hình bình hành đều là hình thoi. Đặc điểm nổi bật là hai cặp cạnh đối song song và các góc đối diện bằng nhau. Ví dụ thực tế có thể kể đến là các viên gạch lát nền hoặc ký hiệu kim cương trong bộ bài.

Bạn có thể tìm hiểu thêm về hình thoi qua các bài viết hướng dẫn trên website toán học. Với điện thoại từ Mytour, việc học trở nên dễ dàng và tiện lợi mọi lúc, mọi nơi. Các mẫu điện thoại giá tốt và ưu đãi hấp dẫn dành cho học sinh, sinh viên tại Mytour chắc chắn sẽ là lựa chọn tuyệt vời cho bạn.
Tính chất của hình thoi là gì?
Hình thoi sở hữu nhiều tính chất đặc trưng. Việc hiểu rõ các tính chất này giúp bạn dễ dàng nhận diện và giải quyết các bài toán hình học liên quan.
- Hình thoi có bốn cạnh đều bằng nhau.
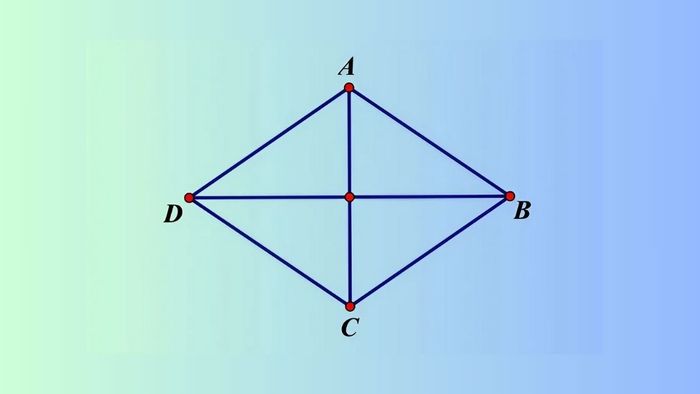
- Hai đường chéo của hình cắt nhau tại trung điểm và tạo thành góc vuông.
- Trục đối xứng của hình là hai đường chéo, chia hình thành bốn tam giác vuông có diện tích bằng nhau.
- Các góc đối trong hình thoi bằng nhau, và tổng hai góc kề nhau luôn là 180 độ.
- Hình thoi là trường hợp đặc biệt của hình bình hành, nên nó thừa hưởng các tính chất của hình bình hành, bao gồm hai cặp cạnh đối song song và các góc đối bằng nhau.
Cách nhận biết hình thoi
Để xác định xem một tứ giác có phải là hình thoi không, bạn có thể dựa vào những dấu hiệu sau:
- Tứ giác có bốn cạnh đều nhau.
- Hai đường chéo của hình cắt nhau tại góc vuông.
- Đường chéo của hình thoi là trục đối xứng của nó.
- Các cặp cạnh kề nhau song song và có độ dài bằng nhau.
Các dấu hiệu này giúp bạn nhanh chóng nhận diện hình thoi, đặc biệt khi làm các bài tập hình học trong trường. Chúng còn hỗ trợ phân biệt hình thoi với các hình khác, giúp việc giải bài tập chính xác và dễ dàng hơn.

Các công thức liên quan đến hình thoi
Để hiểu rõ về hình thoi, chúng ta cần nắm vững các công thức cơ bản, trong đó hai công thức quan trọng nhất là tính diện tích và chu vi của hình thoi. Dưới đây, chúng ta sẽ tìm hiểu chi tiết cách tính diện tích và chu vi hình thoi.
Công thức tính chu vi hình thoi
Để tính chu vi của hình thoi, bạn chỉ cần biết độ dài một cạnh.
Công thức: C = 4 × a
Giải thích:
- C là chu vi của hình thoi.
- a là độ dài của một cạnh của hình thoi.

Với phương pháp này, bạn có thể tính chu vi của bất kỳ hình thoi nào chỉ cần biết độ dài một cạnh. Đây là cách đơn giản, dễ áp dụng trong hình học và rất hiệu quả trong việc giải quyết các bài toán về hình thoi trong học tập và thực tế.
Công thức tính diện tích hình thoi
Diện tích hình thoi được tính bằng cách lấy tích của độ dài hai đường chéo, sau đó chia đôi. Cặp đường chéo của hình thoi cắt nhau tại trung điểm.
Công thức: S = 1/2 × d1 × d2
Giải thích:
- S là diện tích của hình thoi.
- d1 và d2 là độ dài của hai đường chéo.
Bài tập ứng dụng về hình thoi
Dưới đây là một số bài tập mẫu để giúp bạn ôn lại kiến thức về tính chất và diện tích hình thoi.
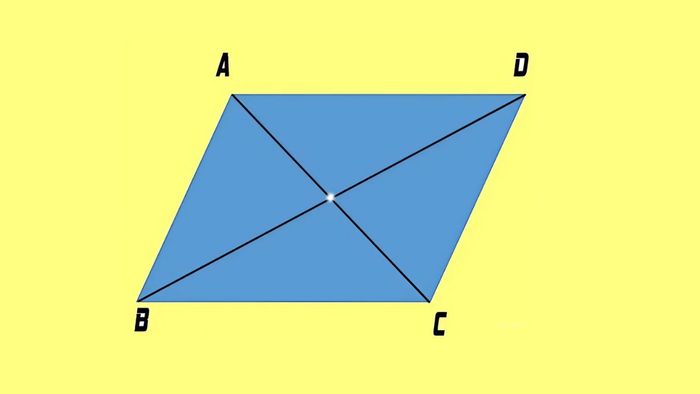
Bài tập 1: Cho hình thoi ABCD có chiều dài cạnh là 7 cm. Tính chu vi của hình.
Lời giải: Chu vi của hình thoi ABCD là: C = 4 × 7 = 28 (cm)
Vậy chu vi của hình thoi ABCD là 28 cm.
Bài tập 2: Cho hình thoi CDFA có độ dài hai đường chéo lần lượt là 10 cm và 12 cm. Tính diện tích của hình thoi.
Lời giải: Diện tích hình thoi CDFA là: S = 1/2 × 10 × 12 = 60 cm²
Do đó, diện tích của hình thoi CDFA là 60 cm².
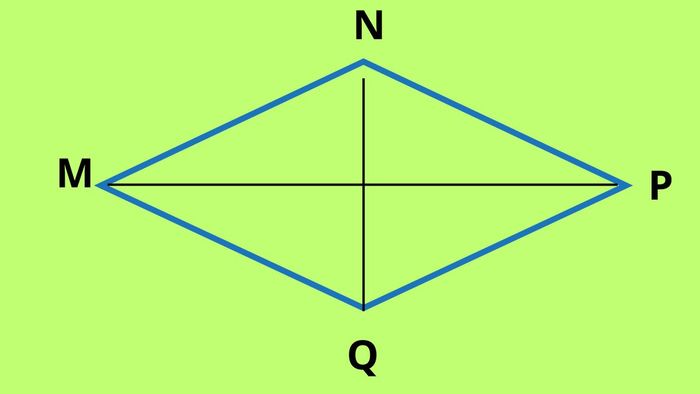
Bài tập 3: Cho hình thoi MNPQ, biết rằng MN = 5 cm và góc MNP = 60°. Tính diện tích của hình MNPQ.
Lời giải: Để tính diện tích hình thoi MNPQ khi biết độ dài cạnh và một góc, ta áp dụng công thức: Diện tích = a² × sin(θ)
Với a = 5 cm và θ = 60°
Diện tích = 1/2 × 5 × 2 × sin(60°) ≈ 21.65 cm²
Vậy diện tích của hình MNPQ là 21.65 cm².
