Việc nắm rõ khái niệm về hai góc bù nhau là điều quan trọng trong việc giải các bài tập hình học. Đây là kiến thức cơ bản nhưng rất cần thiết để xử lý nhiều bài toán. Mytour sẽ giải thích khái niệm hai góc bù nhau và cung cấp một số bài tập mẫu để bạn dễ dàng tham khảo.
Khái niệm hai góc bù nhau là gì?
Hai góc bù nhau là hai góc mà tổng của chúng bằng 180 độ. Khi ghép chúng lại với nhau, chúng tạo thành một đường thẳng. Các góc bù nhau được sử dụng trong nhiều bài toán hình học, đặc biệt là khi tính toán các giá trị góc. Dưới đây là ví dụ và các tính chất liên quan đến kiến thức này.
Ví dụ về hai góc bù nhau
Để giúp bạn dễ dàng hiểu rõ về góc bù nhau, Mytour sẽ đưa ra ví dụ minh họa như sau: Nếu một góc có độ lớn là 70 độ thì góc bù của nó sẽ là 110 độ, vì tổng của chúng là 180 độ (70 + 110 = 180). Tương tự, nếu bạn có một góc 80 độ và một góc 100 độ, chúng sẽ bù nhau tạo thành tổng 180 độ và khi nối lại, chúng sẽ tạo thành một đường thẳng.
Từ đó, ta có thể rút ra công thức cho hai góc bù nhau như sau:
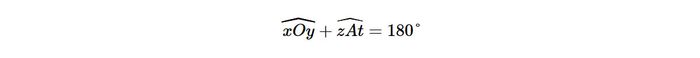
Trong thời đại công nghệ ngày nay, việc học sinh sở hữu laptop là vô cùng quan trọng để nâng cao kỹ năng công nghệ thông tin. Thiết bị này còn hỗ trợ các ứng dụng và phần mềm hữu ích, giúp việc học tập, tìm kiếm thông tin và kết nối trở nên hiệu quả hơn. Với nhiều mẫu mã và mức giá phong phú, bạn có thể dễ dàng sở hữu chiếc laptop chất lượng với mức giá hấp dẫn tại Mytour, đặc biệt là các ưu đãi dành cho học sinh - sinh viên.
Tính chất của hai góc bù nhau
Sau khi bạn đã nắm rõ khái niệm về hai góc bù nhau, tiếp theo là một số tính chất quan trọng mà bạn cần phải hiểu.
- Hai góc chỉ được gọi là góc bù nhau khi tổng của chúng bằng 180°.
- Các góc bù nhau không nhất thiết phải đặt cạnh nhau. Vì vậy, hai góc bất kỳ đều có thể là góc bù nhau nếu tổng của chúng bằng 180° và khi đặt cạnh nhau tạo thành một đường thẳng.
- Ký hiệu chữ "S" trong cụm từ "supplementary angles" (góc bù nhau) mang nghĩa từ "Straight" (thẳng), điều này có nghĩa khi các góc này được ghép lại với nhau, chúng sẽ tạo thành một đường thẳng hoàn chỉnh.
Các loại góc có liên quan
Ngoài việc hiểu rõ về khái niệm hai góc bù nhau, học sinh cũng rất quan tâm đến các góc liên quan khác. Việc nắm vững lý thuyết và tính chất của các góc trong hình học sẽ giúp bạn dễ dàng phân biệt và giải quyết bài tập chính xác hơn. Dưới đây là một số kiến thức bổ sung bạn nên tìm hiểu khi học toán hình.
Hai góc kề nhau
Hai góc kề nhau là hai góc có chung một cạnh và chung một đỉnh. Tổng của hai góc kề nhau không phải lúc nào cũng có giá trị cụ thể, nhưng chúng có một số tính chất sau đây:
- Nếu hai góc kề nhau là góc bù nhau, tổng của chúng sẽ là 180 độ.
- Nếu hai góc kề nhau là góc vuông, tổng của chúng sẽ bằng 90 độ.

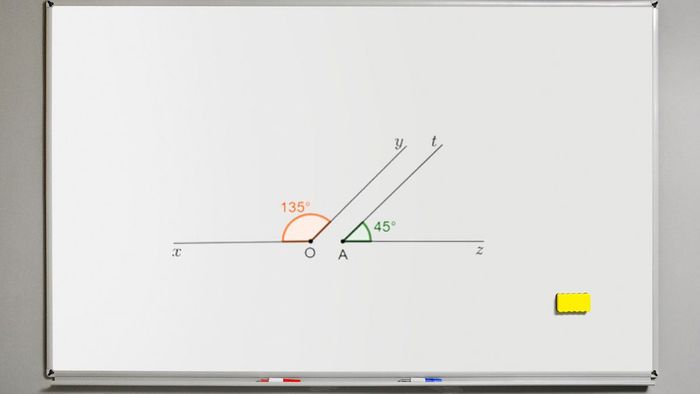
Như trong hình vẽ phía trên, góc xOy và góc yOz có đỉnh chung tại O và cạnh chung là Oy, do đó chúng là hai góc kề nhau.
Hai góc kề bù
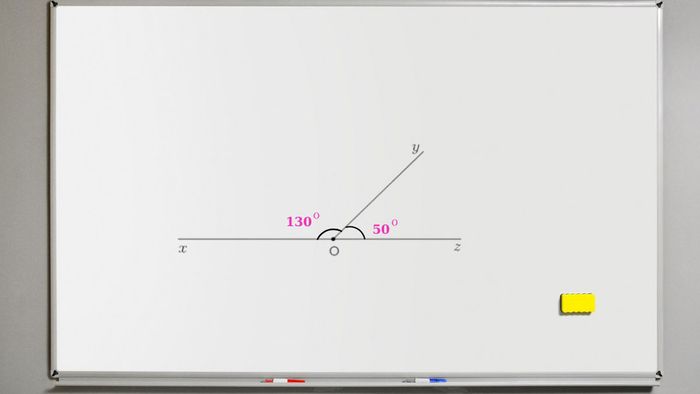
Hai góc được coi là kề bù khi chúng có chung một đỉnh và một cạnh, đồng thời tổng của chúng bằng 180 độ. Như trong hình dưới đây, góc xOy và góc yOz có cạnh Oy chung và đỉnh O chung. Khi cộng số đo của chúng lại, 50 + 130 sẽ bằng 180, điều này chứng minh xOy và yOz là hai góc kề bù vì chúng tạo thành một đường thẳng và có tổng bằng 180 độ.
Bài tập ví dụ về 2 góc bù nhau
Nếu bạn chưa biết cách giải bài tập về hai góc bù nhau, hãy tham khảo một số bài tập mẫu phổ biến dưới đây.
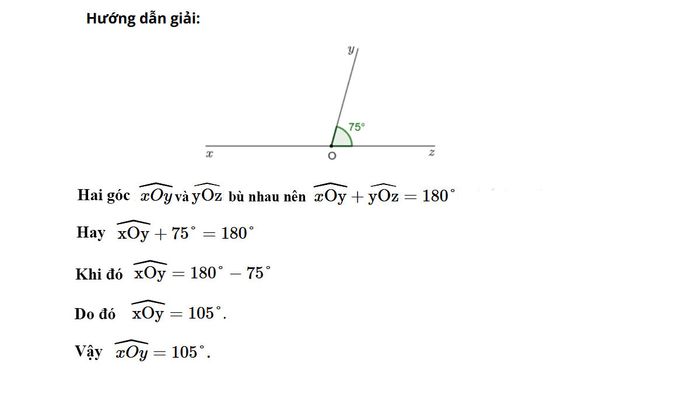
Bài tập 1: Nếu góc xOy và góc yOz bù nhau, trong đó góc yOz có số đo 75 độ, vậy số đo của góc xOy là bao nhiêu?
Bài tập 2: Giải tìm giá trị của góc A và góc B nếu A và B là 2 góc bù nhau, với các phương trình: góc A = 2x + 10 và góc B = 6x – 46?
Hướng dẫn giải
Với tính chất tổng số đo của hai góc bù nhau luôn bằng 180 độ, ta có công thức sau đây:
∠A + ∠B = 180 độ
Công thức trên có thể được viết lại như sau: (2x + 10) + (6x – 46) = 180
Áp dụng phương pháp cộng các hạng tử giống nhau, ta có biểu thức 8x – 36 = 180
Từ đó suy ra: 8x = 180 + 36 = 216
Vậy suy ra: x = 216 / 8 = 27
Với A = 2x + 10 và B = 6x – 46, ta tính được:
∠A = 2.27 + 10 = 64 độ
∠B = 6.27 – 46 = 116 độ
Thông qua phần giải thích về 2 góc bù nhau cùng với các bài tập ví dụ, hy vọng các bạn học sinh đã hiểu rõ hơn về kiến thức hình học này. Bên cạnh việc nắm bắt 2 góc bù nhau và tính chất của chúng, học sinh cũng nên mở rộng thêm nhiều kiến thức khác để áp dụng vào việc giải bài tập một cách hiệu quả. Đừng quên theo dõi các bài viết mới hàng ngày từ Mytour để trang bị thêm kiến thức cho mình về giáo dục nói chung và toán học cùng các môn học khác!
