Những tính chất và dấu hiệu nhận biết tứ giác nội tiếp đóng vai trò nền tảng trong giải toán hình học. Nắm vững và vận dụng chính xác kiến thức này sẽ giúp bạn giải quyết bài toán nhanh chóng và nâng cao khả năng tư duy logic. Bài viết cung cấp các bài tập chứng minh tứ giác nội tiếp kèm lời giải chi tiết, giúp bạn dễ dàng hiểu và áp dụng.
Khái niệm tứ giác nội tiếp
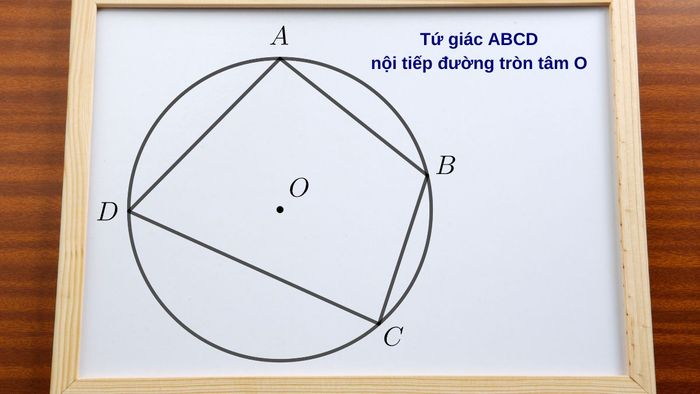
Tứ giác nội tiếp là hình có bốn đỉnh cùng nằm trên một đường tròn, tạo nên mối quan hệ chặt chẽ giữa các góc và cung trong hình. Một tính chất đặc biệt của nó là tổng hai góc đối diện luôn bằng 180 độ. Đây là kiến thức quan trọng trong hình học phẳng, giúp bạn giải quyết các bài toán liên quan đến đường tròn và chứng minh tứ giác nội tiếp.
Trong quá trình học tập, một chiếc Laptop phù hợp là công cụ hỗ trợ đắc lực, giúp bạn làm việc hiệu quả và tiếp cận nguồn tài nguyên dễ dàng. Khám phá ngay những dòng Laptop chất lượng, được ưa chuộng nhất tại Mytour!
Đặc điểm nổi bật của tứ giác nội tiếp
Trong hình học, tứ giác nội tiếp sở hữu nhiều tính chất đặc trưng, được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến chứng minh tứ giác nội tiếp. Dưới đây là một số tính chất quan trọng của dạng hình này:
- Giao điểm của bốn đường trung trực trong tứ giác chính là tâm của đường tròn ngoại tiếp.
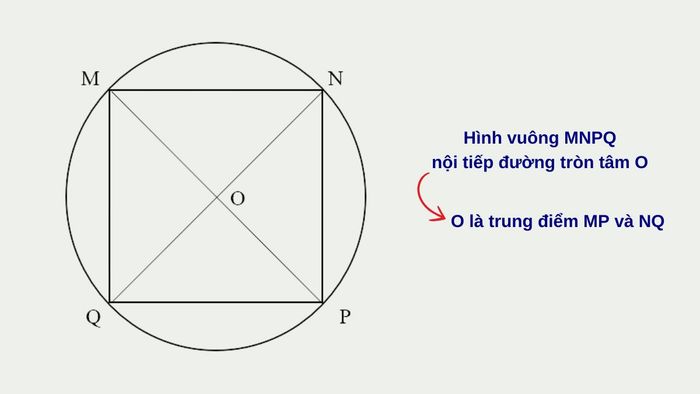
- Nếu hai góc đối diện trong tứ giác nội tiếp vuông góc, trung điểm của đường chéo nối hai đỉnh còn lại sẽ là tâm đường tròn ngoại tiếp.
- Khi hai góc vuông của hình cùng nhìn vào một cạnh, trung điểm của cạnh đó sẽ là tâm đường tròn ngoại tiếp.
Các dấu hiệu giúp nhận biết tứ giác nội tiếp
Trong hình học, việc chứng minh một tứ giác có thể nội tiếp trong đường tròn là bài toán phổ biến. Để làm được điều này, bạn cần dựa vào các đặc điểm hình học đặc trưng. Dưới đây là những dấu hiệu nhận biết tứ giác nội tiếp mà bạn cần lưu ý:
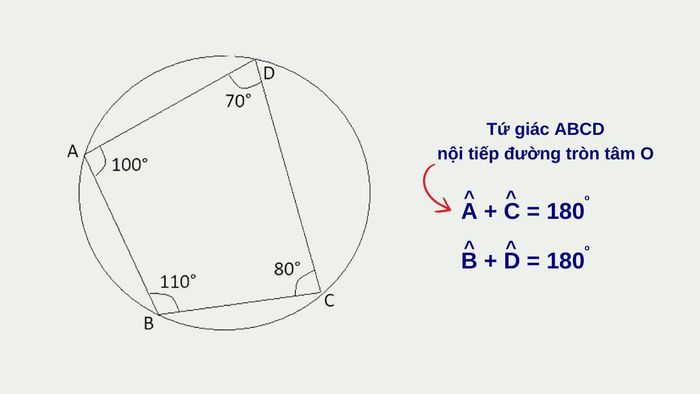
- Nếu tổng hai góc đối diện của tứ giác bằng 180 độ, tứ giác đó có khả năng nội tiếp đường tròn.
- Khi góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện, tứ giác này là tứ giác nội tiếp.
- Nếu khoảng cách từ bốn đỉnh của tứ giác đến một điểm cố định bằng nhau, điểm đó chính là tâm đường tròn ngoại tiếp.
- Nếu hai góc kề nhau cùng nhìn một cạnh với góc bằng nhau, tứ giác đó là tứ giác nội tiếp.
- Các hình như hình chữ nhật, hình vuông và hình thang cân đều là tứ giác nội tiếp.
Các bài tập liên quan đến tứ giác nội tiếp
Tứ giác nội tiếp là một chủ đề quan trọng, thường xuất hiện trong các bài toán chứng minh hình học. Những bài tập này không chỉ rèn luyện tư duy logic mà còn giúp củng cố kiến thức về tính chất và dấu hiệu nhận biết tứ giác nội tiếp. Dưới đây là hai dạng bài tập phổ biến thường gặp khi làm việc với tứ giác nội tiếp.
Dạng 1: Chứng minh tứ giác nội tiếp
Bài toán chứng minh tứ giác nội tiếp trong đường tròn là dạng đề phổ biến trong chương trình học. Có nhiều phương pháp để giải quyết bài toán này, và việc lựa chọn phương pháp phù hợp sẽ giúp bạn chứng minh nhanh chóng và hiểu sâu hơn về các tính chất hình học của tứ giác nội tiếp.
- Phương pháp 1: Đây là cách phổ biến nhất. Bạn chỉ cần chứng minh tổng hai góc đối diện của tứ giác bằng 180 độ để khẳng định nó nội tiếp đường tròn.
- Phương pháp 2: Nếu hai đỉnh kề nhau của tứ giác nhìn một cạnh chung dưới cùng một góc, tứ giác đó sẽ nội tiếp.
- Phương pháp 3: Chứng minh góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện, từ đó suy ra tứ giác nội tiếp.
- Phương pháp 4: Chứng minh tồn tại một điểm cách đều bốn đỉnh của tứ giác, điểm đó chính là tâm đường tròn ngoại tiếp, và tứ giác sẽ nội tiếp.
Cho tam giác ABC, vẽ hai đường cao BM và CN cắt nhau tại H. Hãy chứng minh rằng AMHN và BNMC đều là các tứ giác nội tiếp.
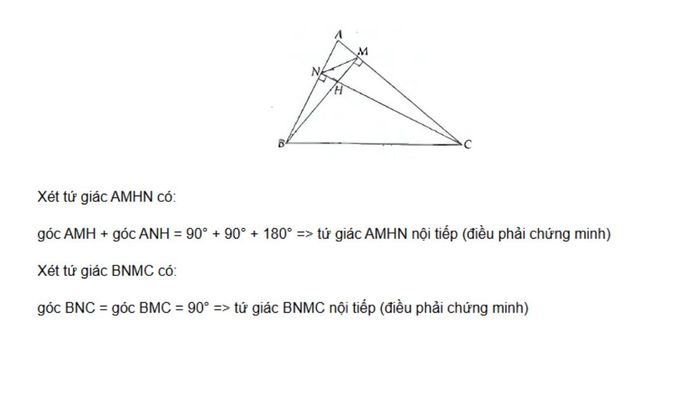
Dạng 2: Ứng dụng tứ giác nội tiếp để chứng minh góc bằng nhau, đoạn thẳng bằng nhau, hoặc các đường thẳng song song
Để giải các bài toán liên quan đến tứ giác nội tiếp, ta sử dụng các tính chất đặc trưng như tổng hai góc đối diện bằng 180 độ, góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung, và các tính chất liên quan đến tâm đường tròn ngoại tiếp.
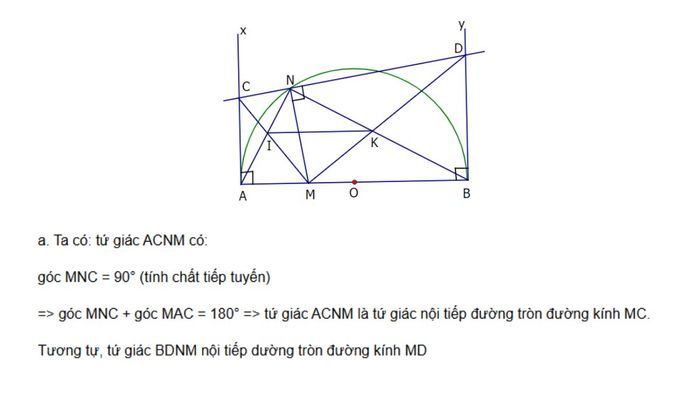
Bài toán: Cho nửa đường tròn tâm O với đường kính AB. Trên đoạn OA, lấy điểm M và trên nửa đường tròn lấy điểm N. Kẻ các tiếp tuyến Ax và By từ A và B. Vẽ đường thẳng qua N vuông góc với NM, cắt Ax và By lần lượt tại C và D. Yêu cầu chứng minh:
a. Tứ giác ACNM và BDNM là các tứ giác nội tiếp.
b. Hai tam giác ANB và CMD đồng dạng. Từ đó, suy ra tứ giác IMKN nội tiếp.

Ví dụ bài tập về tứ giác nội tiếp
Các bài toán hình học dưới đây được chọn lọc kỹ càng, giúp bạn hiểu sâu và vận dụng linh hoạt lý thuyết về tứ giác nội tiếp vào giải toán. Mỗi bài tập chứng minh tứ giác nội tiếp đều đi kèm lời giải chi tiết, giúp bạn nắm rõ cách áp dụng tính chất của dạng hình này trong thực tế.
Ví dụ 1
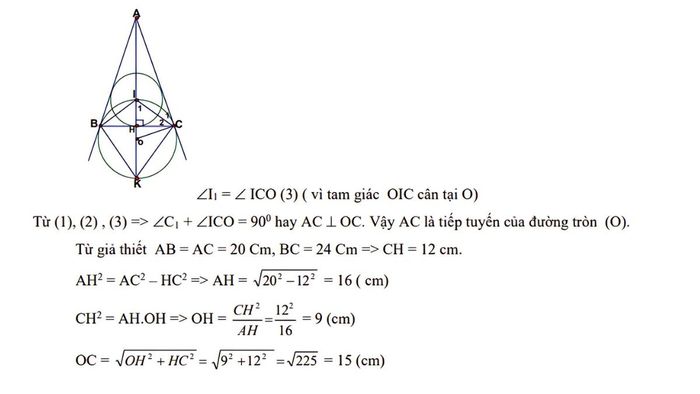
Cho tam giác ABC vuông cân tại A với AB = AC. Gọi I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp tại góc A, và O là trung điểm của đoạn thẳng nối I và K. Cần chứng minh các điều sau:
- Bốn điểm B, C, I, K cùng nằm trên một đường tròn.
- AC là tiếp tuyến của đường tròn (O).
- Tính bán kính đường tròn tâm O, biết AB = AC = 20cm và BC = 24cm.

Ví dụ 2
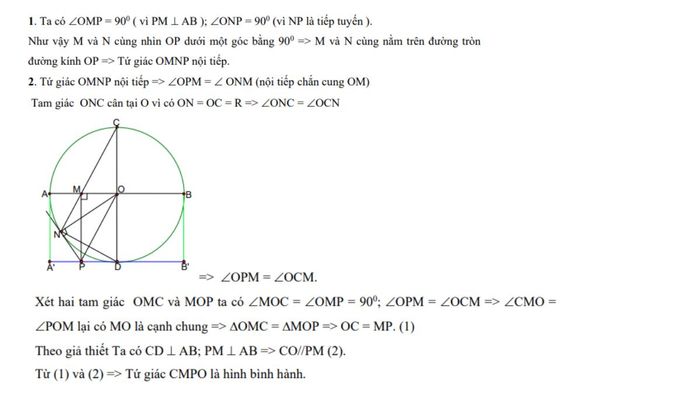
Cho đường tròn (O) bán kính R với hai đường kính AB và CD vuông góc tại O. Trên AB, lấy điểm M khác O. Đoạn CM cắt đường tròn tại N. Kẻ đường thẳng vuông góc với AB tại M, cắt tiếp tuyến tại N của đường tròn tại P. Cần chứng minh:
- Tứ giác OMNP nội tiếp.
- Tứ giác CMPO là hình bình hành.
- Tích CM x CN không đổi khi M di chuyển trên AB.
- Xác định quỹ tích cố định của điểm P khi M thay đổi trên AB.

Ví dụ 3
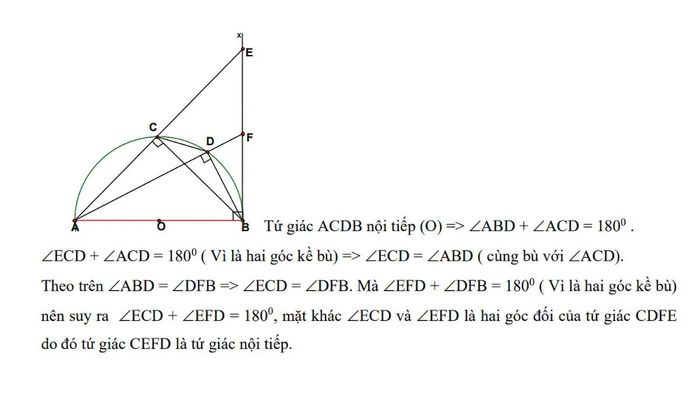
Cho nửa đường tròn (O; R) với đường kính AB. Kẻ tiếp tuyến Bx tại B và chọn hai điểm C, D trên nửa đường tròn. Các tia AC và AD lần lượt cắt Bx tại E và F, với F nằm giữa B và E.
- Chứng minh tích AC × AE không đổi.
- Chứng minh ∠ABD = ∠DFB.
- Chứng minh tứ giác CEFD nội tiếp đường tròn.

Tính chất và dấu hiệu nhận biết tứ giác nội tiếp là kiến thức cốt lõi trong giải toán hình học. Thông qua các bài tập chứng minh tứ giác nội tiếp, bạn sẽ nắm vững phương pháp giải và áp dụng hiệu quả trong học tập và giáo dục. Hãy thường xuyên luyện tập để nâng cao hiểu biết và phát triển tư duy hình học!
