Công thức tính diện tích xung quanh hình trụ không chỉ xuất hiện trong các bài kiểm tra mà còn được áp dụng rộng rãi trong các lĩnh vực thực tế như xây dựng, kiến trúc, công nghiệp,... Bài viết dưới đây sẽ cung cấp chi tiết về cách tính và các dạng bài tập phổ biến liên quan đến diện tích xung quanh hình trụ. Hãy cùng theo dõi để củng cố kiến thức và cải thiện kỹ năng giải quyết bài tập nhé!
Công thức tính diện tích xung quanh hình trụ
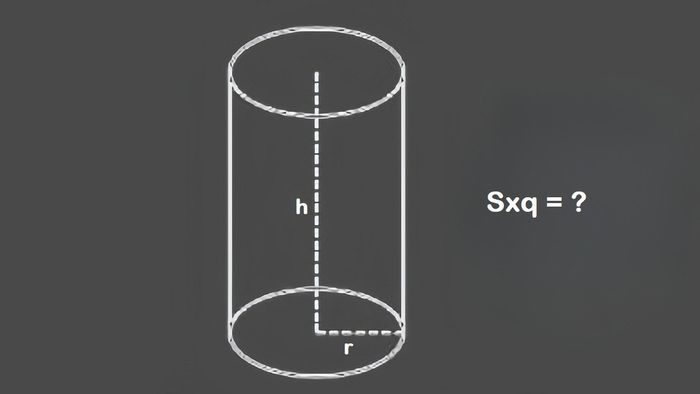
Hình trụ là một thể hình học không gian với hai đáy hình tròn giống nhau, hai cạnh bên song song và có độ dài bằng nhau. Dưới đây là công thức tính diện tích xung quanh của hình trụ giúp bạn giải quyết các bài tập đa dạng.
Sxq = 2 × π × r × h
Trong đó:
- Sxq là ký hiệu diện tích xung quanh của hình trụ;
- Hằng số π với giá trị xấp xỉ ≈ 3,14;
- r là bán kính đáy của hình trụ (hình tròn);
- h là chiều cao của hình trụ.
Ví dụ:
Tính diện tích xung quanh hình trụ, với chiều cao h là 10 cm và bán kính đáy r là 5 cm.
Lời giải:
Áp dụng công thức trên, ta tính được diện tích xung quanh của hình trụ như sau:
Sxq ≈ 2×3,14×10×5 ≈ 314 cm2.
Ngày nay, nhiều phụ huynh đã trang bị máy tính bảng cho con cái để hỗ trợ việc học hiệu quả hơn. Các em có thể dễ dàng tìm thêm các công thức toán học, hóa học, vật lý cùng với các bài tập đa dạng để ôn luyện. Nếu bạn đang tìm mua một chiếc máy tính bảng chất lượng, giá tốt, nhiều ưu đãi, hãy đến Mytour ngay nhé!
Các dạng bài tập liên quan đến diện tích xung quanh hình trụ
Dưới đây là các dạng bài tập (có ví dụ minh họa cụ thể) liên quan đến công thức tính diện tích xung quanh của hình trụ mà Mytour đã tổng hợp. Bạn hãy tham khảo để nắm vững cách áp dụng công thức vào giải các bài tập về hình trụ nhé!
Dạng bài tập tính chiều cao hình trụ
Đây là dạng bài tập cơ bản và phổ biến nhất khi nói đến diện tích xung quanh của hình trụ. Chiều cao hình trụ chính là khoảng cách từ mặt đáy dưới đến mặt đáy trên. Khi bạn đã biết diện tích xung quanh, hãy sử dụng công thức dưới đây để tính chiều cao h của hình trụ:
h = Sxq / (2.π.r)
Ví dụ minh họa:
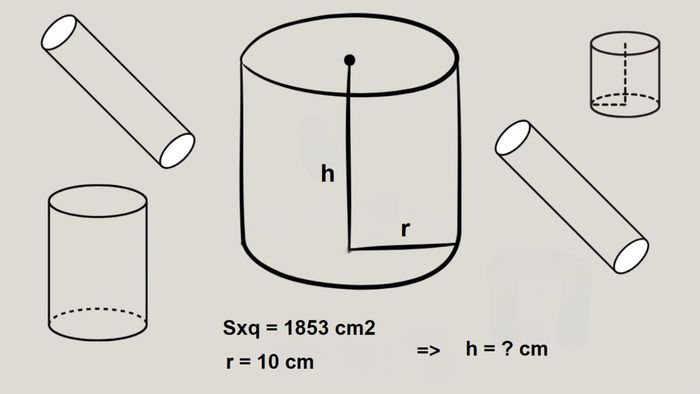
Giả sử một hình trụ có diện tích xung quanh Sxq là 1853 cm2, bán kính đáy r là 10 cm, yêu cầu tính chiều cao h của hình trụ này.
Giải thích:
Áp dụng công thức tính chiều cao h đã biết, ta có chiều cao hình trụ ≈ 1853 / (2×3,14×10) ≈ 29,51 cm.
Dạng bài tập tìm bán kính đáy của hình trụ
Tương tự như việc tính chiều cao của hình trụ, bài toán tính bán kính đáy r cũng khá đơn giản. Khi đề bài cho diện tích xung quanh của hình trụ, để tìm bán kính đáy bạn chỉ cần áp dụng công thức dưới đây:
r = Sxq / (2.π.h)
Ví dụ minh họa:
Cho hình trụ có chiều cao h là 50 cm và diện tích xung quanh Sxq là 6280 cm2, yêu cầu xác định bán kính đáy r của hình trụ.
Giải chi tiết:
Áp dụng công thức, ta có bán kính đáy r = Sxq / (2.π.h) ≈ 6280 / (2×3,14×50) ≈ 20 cm.
Tính diện tích hình trụ khi đáy là đường tròn ngoại tiếp hình tam giác
Đầu tiên, bạn cần tính bán kính đáy của đường tròn ngoại tiếp hình tam giác sử dụng công thức sau đây:
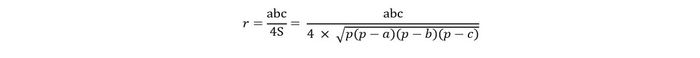
Trong đó:
- a, b, c là độ dài của ba cạnh của tam giác.
- S là diện tích của tam giác.
- p là nửa chu vi tam giác, tính theo công thức: p = (a+b+c) / 2
Sau khi tìm được bán kính đáy, công thức tính diện tích xung quanh hình trụ khi đáy là đường tròn ngoại tiếp hình tam giác như sau:
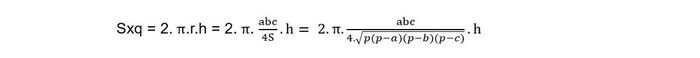
Tìm diện tích xung quanh của một hình trụ có đáy đặc biệt
Ví dụ:
Tính diện tích xung quanh của hình trụ có chiều cao 15 cm, trong đó đáy là một hình tròn ngoại tiếp hình tam giác với ba cạnh lần lượt là 10 cm, 12 cm và 14 cm.
Lời giải:
Áp dụng công thức tính diện tích xung quanh hình trụ, ta có thể giải quyết bài toán này như sau:
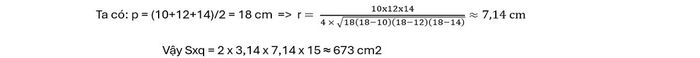
Cách tính diện tích hình trụ khi đáy là một đường tròn nội tiếp trong hình tam giác
Khi đáy của hình trụ là một đường tròn nội tiếp trong hình tam giác, công thức tính diện tích xung quanh sẽ trở nên đơn giản hơn. Sau đây là cách tính bán kính đáy và diện tích xung quanh của hình trụ, bạn có thể theo dõi nhé.

Ví dụ:
Tính diện tích xung quanh của hình trụ có chiều cao 25 cm, với đáy là một đường tròn nội tiếp trong hình tam giác có ba cạnh lần lượt là 6 cm, 10 cm và 12 cm.
Lời giải:
Áp dụng phương pháp tính trên, ta có kết quả như sau:

Bài toán áp dụng công thức tính diện tích hình trụ trong thực tế
Công thức tính diện tích xung quanh của hình trụ rất hữu ích trong nhiều lĩnh vực như xây dựng, công nghệ, và đời sống hàng ngày. Với công thức này, bạn có thể tính toán vật liệu xây dựng, vật liệu trang trí cho các công trình hoặc đồ vật có hình dạng hình trụ. Dưới đây là một số bài tập cùng lời giải giúp bạn hiểu rõ hơn về ứng dụng thực tế của công thức diện tích xung quanh hình trụ.
Bài tập 1: Giả sử bạn cần tính diện tích xung quanh của một ống nước có dạng hình trụ để xác định lượng vật liệu chế tạo ống. Biết đường kính d của ống là 0.6 mét và chiều dài h của ống là 10 mét.
Lời giải:
Bán kính của ống là: r = 0.6/2 = 0.3 m
Vậy diện tích xung quanh của ống nước là: Sxq ≈ 2×3.14×0.3×10 ≈ 18.84 m2

Bài tập 2: Giả sử bạn cần tính diện tích bề mặt ngoài của một bồn chứa nước dạng hình trụ để sơn lại bề mặt của nó. Biết bồn chứa có bán kính đáy r = 3 mét và chiều cao của bồn là h = 5 mét.
Lời giải:
Diện tích cần sơn = 2×π×r×h ≈ 2×3.14×3×5 ≈ 94.2 m2
Dưới đây là công thức và những dạng bài tập thường gặp liên quan đến diện tích xung quanh hình trụ mà bạn không nên bỏ qua. Mytour hy vọng bạn đã hiểu cách áp dụng công thức tính toán trên để giải bài tập và áp dụng trong đo lường, chế tạo vật dụng trong cuộc sống. Hãy theo dõi Mytour để khám phá thêm các công thức toán học, vật lý, hóa học và nhiều kiến thức giáo dục thú vị khác bạn nhé!
