Lũy thừa là một khái niệm toán học cơ bản mà chúng ta gặp trong các bài học từ cấp 2. Nó giúp bạn tính toán nhanh hơn và hiểu sâu hơn về cách các số có thể kết hợp với nhau qua phép nâng lũy thừa.

Lũy thừa là một dạng toán phổ biến trong chương trình học của học sinh. Đây là phép toán mà nhiều bạn học sinh dễ mắc phải những sai sót do những tính chất của nó. Nếu bạn muốn tìm hiểu rõ hơn về lũy thừa bậc n hoặc cần ví dụ cụ thể để hiểu rõ, hãy theo dõi những phần nội dung dưới đây.

Lũy thừa là một phép toán cơ bản trong toán học, thường xuyên xuất hiện trong các bài tập và bài kiểm tra.

Khái niệm về lũy thừa đã quá quen thuộc với học sinh ở cấp trung học. Đây là phép toán quan trọng trong nhiều ngành khoa học như kinh tế, tài chính, hoá học, sinh học, và vật lý.

Nói một cách đơn giản, lũy thừa là phép toán giữa hai yếu tố: cơ số a và số mũ b. Kết quả của phép toán này chính là việc nhân b lần số a với nhau. Công thức lũy thừa được ký hiệu là a^b , đọc là a mũ b hoặc lũy thừa bậc b của a.

Ví dụ về lũy thừa: 5³ đọc là 5 mũ 3 hay lũy thừa bậc 3 của 5. Cơ số ở đây là 5, còn số mũ là 3. Để tính lũy thừa này, bạn nhân ba số 5 lại với nhau.

Để thuận tiện trong việc tính toán và tra cứu các bài toán học, bạn có thể sử dụng laptop. Nếu chưa sở hữu một chiếc laptop, hãy tham khảo những gợi ý mua sắm dưới đây với các chương trình ưu đãi dành cho học sinh, sinh viên.

Phân loại lũy thừa giúp ta dễ dàng hiểu được cách thức và ứng dụng của từng loại trong các bài toán khác nhau.

Sau khi nắm vững khái niệm lũy thừa, bạn sẽ cần phải phân loại các dạng số mũ. Lũy thừa có thể chia thành ba dạng chính: số mũ nguyên, số mũ thực và số mũ hữu tỉ. Mỗi loại có những đặc điểm riêng biệt như sau:

Dạng 1: Lũy thừa với số mũ nguyên

Lũy thừa với số mũ nguyên là dạng thông dụng nhất trong toán học. Với a là một số thực, lũy thừa bậc n (với n là số nguyên) sẽ được tính bằng cách nhân n số a lại với nhau.

Công thức tính lũy thừa bậc n là gì? Bạn có thể áp dụng công thức sau: aⁿ = a x a x a x … x a.

Dạng lũy thừa với số mũ nguyên còn có những tính chất đặc biệt đáng chú ý, bao gồm các công thức cơ bản sau đây:

• a⁰ = 1
• a¹ = a
• 0ⁿ = 0
• 1ⁿ = 1
• a^-n = 1/aⁿ

Dạng 2: Lũy thừa với số mũ thực

Lũy thừa của số thực được ký hiệu là a^α (đọc là a mũ alpha hoặc lũy thừa alpha của a), trong đó α là một số vô tỉ thường gặp trong các bài toán toán học phức tạp.

Khi xét một dãy số hữu tỉ (ký hiệu là r_n) với α = lim r_n, ta có thể thấy rằng dãy số a mũ r_n sẽ có một giới hạn xác định và không phụ thuộc vào giá trị của r_n.

Công thức tính lũy thừa với số mũ thực có thể được biểu diễn như sau: a^α = lim (a mũ r_n).

Dạng 3: Lũy thừa với số mũ hữu tỉ

Lũy thừa với số mũ hữu tỉ, được biểu diễn dưới dạng phân số a/b, là một phép toán quen thuộc trong nhiều ngành học. Với a là một số thuộc tập R và r = m/n (m và n là các số nguyên, n > 0 và a > 0), lũy thừa bậc r của a sẽ được tính bằng công thức sau:

Trường hợp đặc biệt trong lũy thừa với số mũ hữu tỉ có những quy tắc riêng biệt cần chú ý.

Tính chất của lũy thừa là những đặc điểm quan trọng giúp ta giải quyết các bài toán liên quan đến phép toán này một cách hiệu quả.

Ba dạng lũy thừa cơ bản trên chỉ mới cung cấp những công thức cơ bản. Để hiểu rõ hơn về lũy thừa và cách áp dụng nó hiệu quả trong các ngành học khác nhau, bạn cần nắm vững những tính chất quan trọng dưới đây:

Tính chất đẳng thức của lũy thừa có ý nghĩa gì?

Với các hệ số a và b khác 0, m và n thuộc tập R, tính chất đẳng thức của lũy thừa được thể hiện qua các công thức sau:

• a^m x aⁿ = a^m+n
• a^m / aⁿ = a^m-n
• (a^m)ⁿ = a^{m x n}
• (a x b)^m = a^m x b^m
• (a / b)^m = a^m / b^m

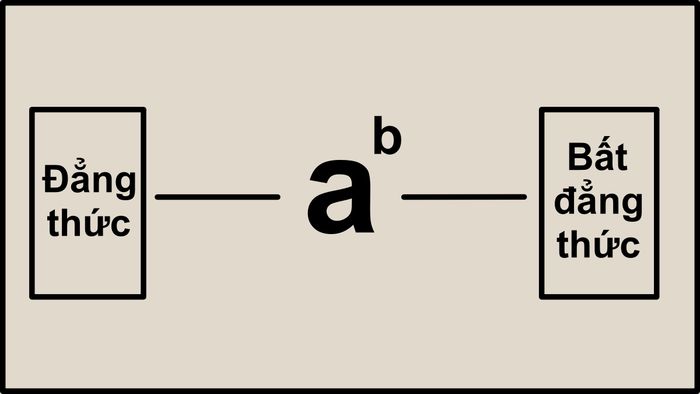
Tính chất này thường gặp trong các bài toán so sánh, đặc biệt là trong các tình huống sau:

Khi m và n đều thuộc tập hợp R, ta có thể so sánh các giá trị cùng cơ số như sau:

• Giả sử a > 1 và a^m > aⁿ, ta suy ra m > n.
• Giả sử 0 < a < 1 và a^m > aⁿ, ta suy ra m < n.

Để so sánh các số mũ, bạn có thể sử dụng công thức sau đây:

• Giả sử số mũ là một giá trị dương và a > b > 0, ta có aⁿ > bⁿ.
• Giả sử số mũ là một giá trị âm và a > b > 0, ta có aⁿ < bⁿ.

Hướng dẫn sử dụng máy tính cầm tay để tính lũy thừa

Máy tính cầm tay là công cụ hữu ích giúp học sinh tính lũy thừa một cách nhanh chóng và chính xác. Dưới đây là cách bạn có thể sử dụng máy tính để giải các bài toán lũy thừa:

Bước 1: Nhấn nút ON để bật máy tính Casio.

Bước 2: Khi màn hình máy tính đã sẵn sàng, bạn nhập phép tính lũy thừa vào máy tính cầm tay. Bạn nhập hệ số đầu tiên, sau đó nhấn nút x mũ trên bàn phím. Tiếp theo, bạn di chuyển con trỏ lên vị trí của mũ và nhập giá trị mũ.

Bước 3: Bạn nhấn dấu bằng và kết quả sẽ xuất hiện ở góc dưới của màn hình máy tính cầm tay.

Một số bài tập về lũy thừa kèm theo đáp án tham khảo

Để dễ dàng nắm bắt phép toán này, bạn có thể tham khảo một số ví dụ bài tập về lũy thừa dưới đây:

Bài 1: So sánh kết quả của hai lũy thừa 2³ và 3²

Bài giải:

Ta có: 2³ = 2 x 2 x 2 = 8 và 3² = 3 x 3 = 9. Như vậy, 2³ nhỏ hơn 3².

Bài 2: Tính giá trị các phép toán sau đây:

a. a⁴ x a⁶

b. (a⁵)⁶

c. (a³)⁴ x a⁹

Bài giải:

a. a⁴ x a⁶ = a^{4 + 6} = a¹⁰

b. (a⁵)⁶ = a^{5 x 6} = a³⁰

c. (a³)⁴ x a⁹ = a¹² x a⁹ = a^{12 + 9} = a²¹

Bài 3: Rút gọn các phương trình dưới đây:

a. 4⁸ x 2²⁰

b. 64³ x 4⁵ x 16²

Bài giải:

a. 4⁸ x 2²⁰ = (2²)⁸ x 2²⁰ = 2¹⁶ x 2²⁰ = 2^{16 + 20} = 2³⁶

b. 64³ x 4⁵ x 16² = (4³)³ x 4⁵ x (4²)² = 4⁹ x 4⁵ x 4⁴ = 4¹⁸

Trên đây là giải thích về lũy thừa là gì, kèm theo ví dụ để bạn dễ hiểu dạng bài này. Đây là dạng bài khá phức tạp, vì vậy bạn hãy ôn luyện kỹ. Nếu muốn tìm hiểu thêm các bài toán khác, hãy tham khảo thêm các bài viết tương tự trên Mytour.