Việc nắm rõ các trường hợp bằng nhau của tam giác vuông là kiến thức hình học nền tảng, hỗ trợ hiệu quả trong việc chứng minh hình học và ứng dụng thực tiễn như xây dựng, đo đạc, thiết kế. Cùng Mytour khám phá các tiêu chí xác định hai tam giác vuông bằng nhau để áp dụng vào bài toán một cách chính xác!
Khái niệm hai tam giác bằng nhau
Hai tam giác được gọi là bằng nhau khi chúng giống hệt nhau về hình dạng và kích thước, tức là ba cạnh tương ứng bằng nhau và ba góc tương ứng cũng bằng nhau.
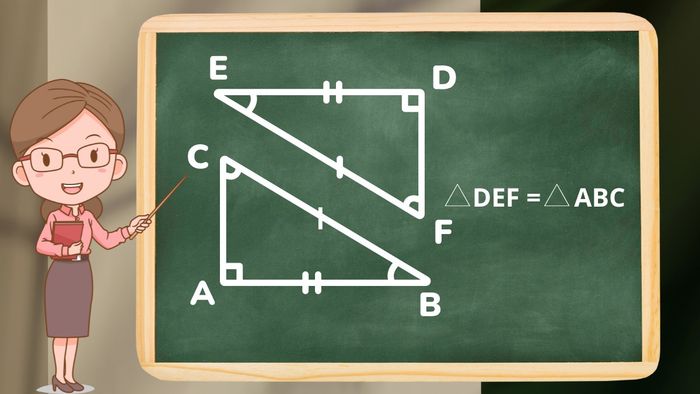
Để biểu thị hai tam giác ABC và DEF bằng nhau, ta dùng ký hiệu △ABC = △DEF. Điều này có nghĩa là:
- Các cạnh tương ứng: AB = DE, BC = EF, AC = DF.
- Các góc tương ứng: ∠BAC = ∠EDF, ∠ABC = ∠DEF, ∠BCA = ∠EFD.
Các trường hợp đặc biệt để hai tam giác vuông bằng nhau
Để biết hai tam giác vuông có bằng nhau không, cần xét các yếu tố như độ dài cạnh và số đo góc. Trong hình học, có 4 trường hợp cơ bản giúp xác định hai tam giác vuông bằng nhau. Cùng Mytour tìm hiểu ngay sau đây:
Trường hợp hai cạnh góc vuông bằng nhau
Nếu hai tam giác vuông có hai cạnh góc vuông tương ứng bằng nhau thì có thể khẳng định chúng bằng nhau. Đây là một trong bốn trường hợp bằng nhau của tam giác vuông, gọi là cạnh - góc - cạnh (c-g-c). Ví dụ: △ABC vuông tại A và △DEF vuông tại D có AB = DE, AC = DF thì suy ra △ABC = △DEF.
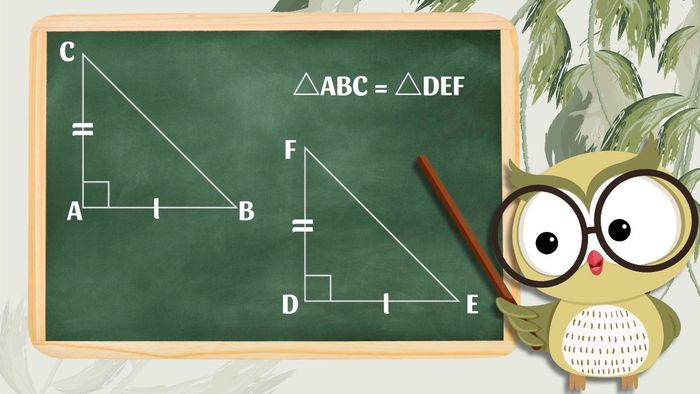
Một cạnh góc vuông và góc nhọn kề cạnh đó
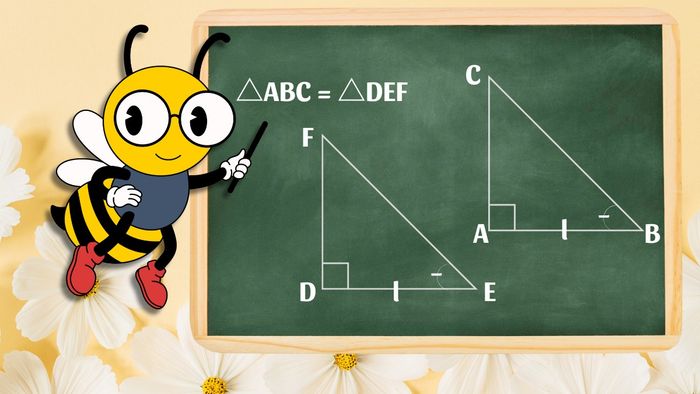
Hai tam giác vuông bằng nhau khi có một cạnh góc vuông bằng nhau và góc nhọn kề cạnh đó cũng bằng nhau. Đây là trường hợp góc - cạnh - góc (g-c-g) trong chứng minh hình học. Ví dụ: △ABC vuông tại A và △DEF vuông tại D có AB = DE, ∠ABC = ∠DEF thì suy ra △ABC = △DEF.
Muốn học tốt môn Toán, ghi chú nhanh và giải bài dễ dàng? iPad sẽ là công cụ hỗ trợ lý tưởng cho việc vẽ hình, ghi chép, tra cứu và luyện tập mọi lúc mọi nơi. Khám phá ngay các mẫu iPad chính hãng tại Mytour qua đường link bên dưới. Đừng bỏ lỡ!
Trường hợp có cạnh huyền và một góc nhọn
Hai tam giác vuông được xem là bằng nhau khi có cùng chiều dài cạnh huyền và một cặp góc nhọn bằng nhau. Đây là trường hợp g-c-g (góc - cạnh - góc) trong chứng minh tam giác. Khi cạnh huyền và một góc nhọn đã xác định, hình dạng tam giác cố định, từ đó suy ra △ABC = △DEF nếu △ABC vuông tại A, △DEF vuông tại D, BC = EF và ∠ABC = ∠DEF.

Trường hợp có cạnh huyền và một cạnh góc vuông
Hai tam giác vuông được coi là bằng nhau nếu có cạnh huyền bằng nhau và một cạnh góc vuông tương ứng cũng bằng nhau. Đây là một trường hợp đặc biệt trong các tiêu chí chứng minh tam giác vuông bằng nhau. Ví dụ: △ABC vuông tại A và △DEF vuông tại D, nếu BC = EF và AB = DE thì suy ra △ABC = △DEF.

Một số bài tập ví dụ
Dưới đây là các bài tập áp dụng để chứng minh các trường hợp tam giác vuông bằng nhau.
Bài 1: Cho tam giác △MNP cân tại M, đoạn thẳng MH vuông góc với NP. Hãy chứng minh:
- a) HN bằng HP.
- b) Góc ∠NMH bằng góc ∠PMH.
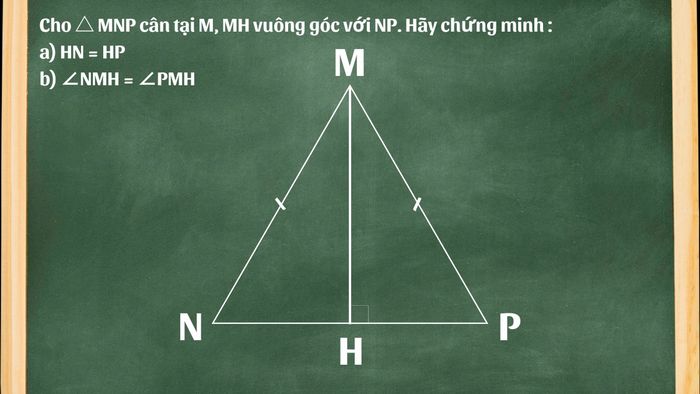
Hướng dẫn giải:
- a) Xét hai tam giác △MNH và △MPH, ta có:
MN = MP và AH là cạnh chung. Do đó, △MNH = △MPH theo trường hợp cạnh huyền - cạnh góc vuông.
Suy ra HN = HP.
- b) Từ kết quả trên, ta có △MNH = △MPH nên ∠NMH = ∠PMH.
Bài 2: Cho tam giác vuông △ABC vuông tại A và △MNP vuông tại M, biết AC = MP. Hãy xác định các trường hợp bằng nhau của hai tam giác này.
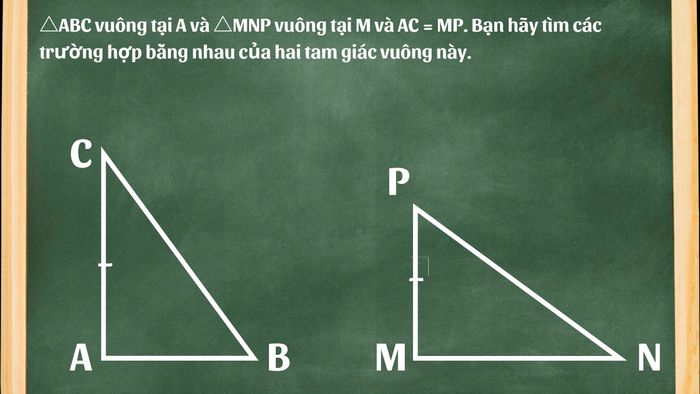
Hướng dẫn giải:
Nếu AB = MN thì △ABC = △MNP theo trường hợp cạnh - góc - cạnh (c-g-c).
Nếu ∠ACB = ∠MPN thì △ABC = △MNP theo trường hợp góc - cạnh - góc (g-c-g).
Nếu BC = NP thì △ABC = △MNP theo trường hợp cạnh huyền - cạnh góc vuông.
Bài 3: Cho tam giác △DEF cân tại D, với ∠D < 90°. Vẽ EK vuông góc với DF (K thuộc DF), và FH vuông góc với DE (H thuộc DE).
- a) Chứng minh rằng DK = KH.
- b) Giao điểm M của EK và FH, hỏi DM có phải tia phân giác của góc D không?
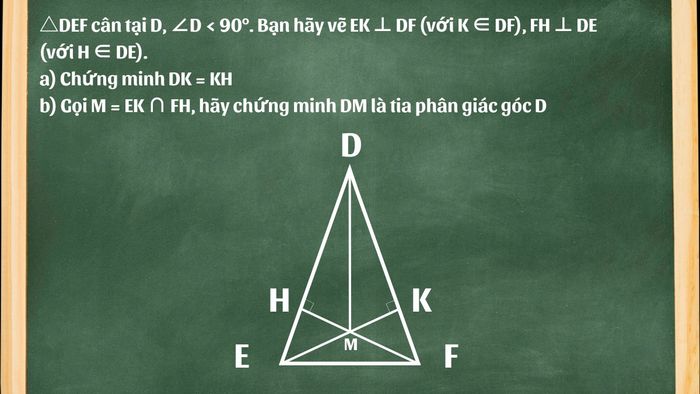
Phần giải:
- a) Tam giác △DEF cân tại D nên ta có DE = DF.
Xét hai tam giác △KDE và △HDF, ta thấy:
DE = DF và góc D là góc chung giữa hai tam giác.
Do đó, △KDE = △HDF theo trường hợp cạnh huyền - góc nhọn.
=> các cạnh tương ứng DK = DH.
- b) Xét tam giác △HDM và △KDM, ta có:
DK = DH
DM là cạnh chung của hai tam giác.
=> △KDM = △HDM theo trường hợp cạnh huyền - cạnh góc vuông và ∠KDM = ∠HDM nên tia DM là tia phân giác của góc D.
Mytour đã trình bày chi tiết các trường hợp bằng nhau của tam giác vuông kèm theo những bài tập minh họa hữu ích. Đây là dạng toán phổ biến giúp phát triển tư duy logic và tạo nền tảng vững chắc cho môn hình học. Việc thành thạo các quy tắc này sẽ giúp bạn giải bài chính xác và hiệu quả hơn. Để cập nhật thêm các bài toán và công thức mới, bạn hãy truy cập chủ đề Giáo dục của Mytour nhé!
Xem thêm bài viết cùng chuyên mục: Góc Học & Dạy 4.0
