Phương pháp tìm giá trị nhỏ nhất của hàm số lớp 12 là kiến thức trọng tâm hỗ trợ học sinh giải nhiều dạng bài. Để đạt kết quả chính xác, cần áp dụng các kỹ thuật như phân tích miền xác định và sử dụng định lý toán phù hợp. Cùng Mytour khám phá cách giải đa dạng giúp bạn tự tin làm bài khi gặp dạng toán này!
Khái niệm giá trị nhỏ nhất của hàm số
Trong Toán học, giá trị nhỏ nhất của hàm số là mức thấp nhất mà hàm có thể đạt được trên miền xác định hoặc đoạn nhất định. Cụ thể, nếu f(x) đạt giá trị m tại điểm x0 thuộc miền D và không tồn tại giá trị nào nhỏ hơn m, thì m chính là giá trị cực tiểu của hàm trên D.
Việc xác định giá trị nhỏ nhất đóng vai trò thiết yếu trong nhiều bài toán thực tế như tối ưu chi phí, tính toán hiệu suất hoặc tìm đại lượng cực tiểu trong vật lý. Hiểu đúng bản chất và nắm chắc phương pháp sẽ giúp học sinh xử lý hiệu quả các bài toán liên quan.

Cách tìm giá trị nhỏ nhất của hàm số
Có nhiều phương pháp để tìm giá trị nhỏ nhất của hàm số lớp 12, phụ thuộc vào miền xác định mà bài toán yêu cầu. Trong chương trình Toán lớp 12, hai dạng bài phổ biến nhất thường yêu cầu cách giải khác nhau.
Phương pháp tìm giá trị nhỏ nhất trên miền xác định D
Để xác định giá trị nhỏ nhất trên miền D, thường dùng đạo hàm để tìm các điểm tới hạn - những điểm có thể là cực tiểu hoặc cực đại. Tiếp theo, phân tích bảng biến thiên để xác định giá trị nhỏ nhất.
Đôi khi, giá trị cực tiểu không nằm tại điểm tới hạn mà ở biên miền xác định. Ví dụ, với hàm số:
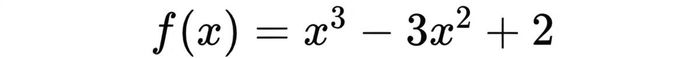
Bạn cần tính đạo hàm, tìm nghiệm bằng 0 rồi xét dấu để xác định chiều biến thiên. Cuối cùng, so sánh giá trị hàm tại các điểm này để tìm giá trị nhỏ nhất chính xác.
Để học tập và giải Toán hiệu quả hơn, iPad kèm Apple Pencil là công cụ tuyệt vời. Với khả năng take note mượt mà, bạn có thể ghi chú công thức, vẽ đồ thị và lưu tài liệu cách giải các bài toán tìm giá trị nhỏ nhất một cách khoa học. Hãy tham khảo các dòng iPad mới nhất để chinh phục Toán dễ dàng hơn:
Phương pháp tìm giá trị lớn nhất và nhỏ nhất trên một đoạn
Cách xác định giá trị nhỏ nhất của hàm số trên đoạn [a,b] là xét cả điểm tới hạn và giá trị tại hai đầu đoạn. Sau khi tính đạo hàm và tìm nghiệm bằng 0, so sánh các giá trị này để chọn ra giá trị nhỏ nhất. Ví dụ, xét hàm:
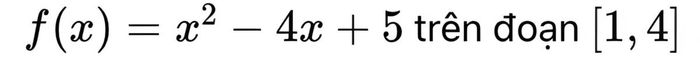
Bạn cần tính đạo hàm, tìm điểm tới hạn x=2, rồi tính giá trị f(x) tại các điểm x=1, 2, 4. So sánh các giá trị này để xác định giá trị lớn nhất và nhỏ nhất trên đoạn.

Các dạng bài tập và cách giải phổ biến
Trong chương trình Toán lớp 12, việc tìm giá trị nhỏ nhất của hàm số là nội dung thiết yếu. Để giải đúng các bài tập này, học sinh cần hiểu rõ các dạng bài thường gặp và phương pháp giải thích hợp.
Phương pháp tìm giá trị nhỏ nhất của hàm số
Bạn cần xác định chiều biến thiên của hàm số và tìm điểm mà giá trị đạt nhỏ nhất. Một trong những cách phổ biến là dùng đạo hàm để xác định các điểm giới hạn.
Những điểm này có thể là cực tiểu hoặc không, nên cần kiểm tra kỹ sự biến thiên để đưa ra kết luận chính xác. Ví dụ, xét hàm số:
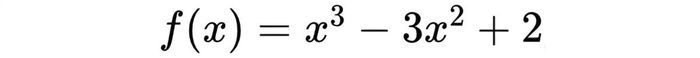
Đầu tiên, bạn cần tính đạo hàm để xác định các điểm tới hạn. Sau khi có các điểm nghi là cực tiểu, hãy kiểm tra dấu đạo hàm để khẳng định điểm nào là giá trị nhỏ nhất thực sự. Ngoài ra, trong một số trường hợp đặc biệt, giá trị nhỏ nhất có thể nằm ở biên miền xác định thay vì tại điểm tới hạn.
Cách tìm giá trị nhỏ nhất của hàm số trên đoạn
Khi tìm giá trị nhỏ nhất trên đoạn [a,b], cần xét cả điểm tới hạn và giá trị hàm tại hai đầu đoạn. Do vậy, phương pháp tìm giá trị nhỏ nhất trên đoạn có sự khác biệt so với việc xét trên toàn miền xác định. Ví dụ, với hàm số:
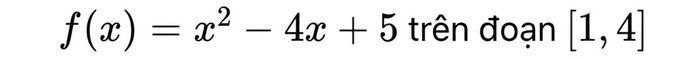
Đầu tiên, tính đạo hàm và xác định điểm tới hạn x=2. Tiếp theo, tính giá trị hàm tại x=2 và hai đầu đoạn x=1, x=4. So sánh các giá trị này để tìm ra giá trị nhỏ nhất trên đoạn cho trước.

Cách tìm giá trị nhỏ nhất của hàm số lượng giác
Hàm số lượng giác có tính tuần hoàn, vì vậy khi tìm giá trị nhỏ nhất cần chú ý chu kỳ và miền xác định. Các hàm lượng giác thường gặp bao gồm sinx, cosx, tanx và các tổ hợp liên quan.
Giả sử cần xác định đại lượng cực tiểu của hàm số:
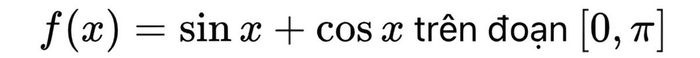
Trước hết, tính đạo hàm và tìm nghiệm phương trình đạo hàm bằng 0 để xác định điểm tới hạn. Sau đó, so sánh giá trị hàm tại điểm này và hai đầu đoạn để tìm giá trị nhỏ nhất thật sự.
Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trong các bài toán đặc biệt
Ngoài các bài toán tìm giá trị nhỏ nhất hàm số lớp 12 thông thường, còn có nhiều dạng bài đặc biệt yêu cầu linh hoạt trong cách giải. Ví dụ, với hàm số chứa dấu giá trị tuyệt đối, bất đẳng thức hay tham số, việc tìm giá trị nhỏ nhất sẽ phức tạp hơn. Xem xét ví dụ:
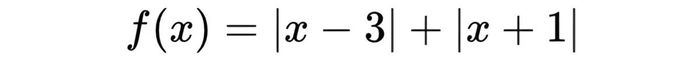
Với dạng bài này, không thể áp dụng đạo hàm trực tiếp. Thay vào đó, cần phân chia miền xác định thành các khoảng, xét biểu thức trong từng khoảng rồi so sánh giá trị hàm tại các điểm biên để xác định giá trị nhỏ nhất.
Nắm chắc cách tìm giá trị nhỏ nhất của hàm số lớp 12 giúp bạn giải nhanh nhiều dạng bài tập quan trọng. Hãy áp dụng linh hoạt các phương pháp đã học và luyện tập đều đặn để tự tin hơn trong các kỳ thi quan trọng.
