Trong toán học, nguyên hàm là một chủ đề quan trọng mà bất kỳ ai nghiên cứu chuyên sâu đều phải đối mặt. Nhiều người đặc biệt quan tâm đến các công thức, phương pháp và cách giải bài tập nguyên hàm từng phần, đặc biệt khi gặp phải những hàm số phức tạp. Trong bài viết này, chúng ta sẽ cùng tìm hiểu chi tiết về dạng toán này, cách giải nhanh và các mẹo giúp việc giải toán trở nên dễ dàng hơn.
Khái niệm nguyên hàm từng phần
Nguyên hàm từng phần là kỹ thuật giúp tính nguyên hàm của tích hai hàm số bằng cách chia nhỏ chúng và tính toán từng phần riêng biệt. Phương pháp này đặc biệt hữu ích khi bạn gặp phải các nguyên hàm phức tạp, chẳng hạn như tích của hàm đa thức với hàm lượng giác hoặc hàm liên quan đến logarithm.

Hãy hình dung bạn đang phải giải quyết một bài toán với những biểu thức rắc rối và cần tìm cách đơn giản hóa chúng. Bằng cách chia nhỏ vấn đề và giải quyết từng phần, mọi thứ sẽ trở nên dễ dàng hơn. Dạng toán này cũng hoạt động dựa trên nguyên lý tương tự!
Phương pháp tính nguyên hàm từng phần
Khi đối mặt với một bài toán nguyên hàm dạng tích của hai hàm số, bạn có thể cảm thấy bối rối không biết bắt đầu từ đâu. Đừng lo lắng! Công thức nguyên hàm từng phần sẽ là công cụ hữu hiệu giúp bạn giải quyết sự phức tạp và tìm ra đáp án một cách nhanh chóng.
Công thức tính toán
Hãy hình dung bạn đang phải giải quyết một bài toán với những biểu thức phức tạp và cần tìm cách đơn giản hóa chúng một cách nhanh chóng. Để làm được điều này, chúng ta sẽ cùng tìm hiểu công thức tổng quát, giúp bạn áp dụng dễ dàng vào các bài toán thực tế. Công thức tổng quát cho nguyên hàm từng phần sẽ được trình bày chi tiết như sau:

Giải thích công thức
Trước khi bắt đầu chứng minh công thức nguyên hàm từng phần, hãy cùng suy ngẫm: Nếu chúng ta biết cách tính đạo hàm của tích hai hàm số, liệu có thể áp dụng ngược lại để tìm nguyên hàm không? Để thực hiện, bạn cần nhớ lại quy tắc đạo hàm của tích hai hàm. Từ đó, chúng ta có thể điều chỉnh linh hoạt để tìm ra công thức phù hợp cho từng dạng bài toán cụ thể.

Mẹo hữu ích khi giải bài tập nguyên hàm từng phần
Khi giải các bài tập này, nhiều người thường mắc sai lầm trong việc chọn u và dv không phù hợp, khiến quá trình tính toán trở nên rắc rối. Bên cạnh đó, lỗi trong việc tính đạo hàm hoặc nguyên hàm phụ cũng khá phổ biến. Đặc biệt, việc quên cộng hằng số C thường dẫn đến kết quả sai lệch:
1. Một trong những quy tắc phổ biến giúp xác định thứ tự ưu tiên khi chọn hàm là quy tắc LIATE.

2. Kiểm tra kết quả: Sau khi tính toán, hãy đạo hàm lại kết quả để đảm bảo tính chính xác.

3. Thử phương pháp khác: Nếu cách tính nguyên hàm từng phần gặp khó khăn, hãy thử thay đổi cách chọn u và dv.

Một số ví dụ bài tập minh họa
Phương pháp nguyên hàm từng phần là một công cụ quan trọng trong giải tích, giúp tính toán các nguyên hàm dạng tích của hai hàm số. Dưới đây là một số bài tập minh họa kèm lời giải chi tiết, giúp bạn hiểu rõ cách áp dụng dạng toán phức tạp này vào thực tế.
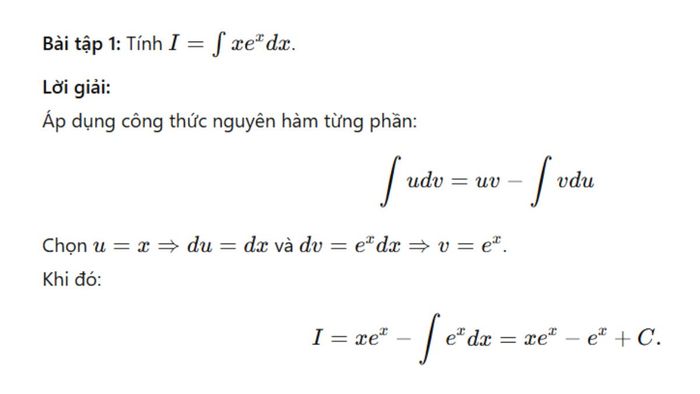
Khi giải bài tập này, cần chú ý chọn u và dv một cách hợp lý để quá trình tính toán trở nên đơn giản. Thông thường, ưu tiên chọn u là hàm số giảm bậc sau khi lấy đạo hàm, chẳng hạn như đa thức hoặc hàm logarithm. Đồng thời, cần kiểm tra kỹ kết quả nguyên hàm phụ để tránh sai sót. Trong trường hợp bài toán phức tạp, bạn có thể áp dụng phương pháp này nhiều lần để đạt kết quả chính xác.
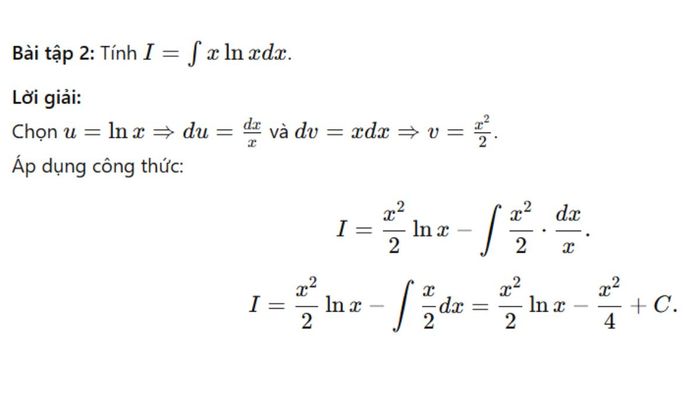
Trên đây là công thức, phương pháp và cách giải bài tập nguyên hàm từng phần, giúp bạn nhận ra rằng toán học cũng có thể rất thú vị! Khi nắm vững phương pháp này, việc giải các bài toán tích phân sẽ trở nên đơn giản hơn rất nhiều. Bạn sẽ cảm thấy tự tin hơn khi xử lý các dạng toán phức tạp sau khi nắm được các mẹo và công thức tính toán. Toán học tuy là một lĩnh vực khó trong giáo dục, nhưng chỉ cần kiên trì luyện tập, bạn sẽ giải quyết được nhiều dạng bài tập hơn.
Khám phá thêm các bài viết liên quan: Góc Học & Dạy 4.0
