Công thức và cách tính tích phân từng phần là công cụ hữu ích để xử lý các bài toán tích phân khó. Kỹ thuật này là sự mở rộng từ quy tắc tích phân cơ bản, giúp biến đổi các biểu thức phức tạp thành dạng đơn giản hơn. Nắm vững phương pháp này sẽ giúp bạn tự tin giải quyết các bài tập tích phân từng phần đầy thử thách.
Khái niệm tích phân từng phần
Đây là kỹ thuật toán học giúp biến đổi các bài toán tích phân phức tạp thành dạng dễ giải quyết hơn. Phương pháp này dựa trên mối quan hệ giữa đạo hàm và nguyên hàm. Cụ thể, biểu thức ban đầu được chia thành hai phần: một phần được lấy đạo hàm và phần còn lại được lấy nguyên hàm. Thông thường, dạng bài này liên quan đến tích phân của hai trong bốn loại hàm: đa thức, logarit, lượng giác và hàm mũ.

Công thức tích phân từng phần và cách chứng minh công thức
Việc áp dụng chính xác công thức sẽ giúp bạn giải quyết hiệu quả các bài toán tích phân phức tạp. Dưới đây là công thức cùng với phần chứng minh chi tiết mà Mytour cung cấp, giúp bạn hiểu rõ hơn về phương pháp này.
Công thức tính tích phân từng phần:
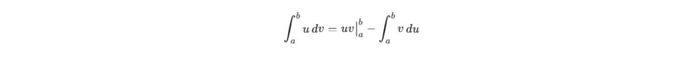

Chứng minh: Bắt nguồn từ quy tắc vi phân của tích phân hai hàm số u(x) và v(x): d(uv) = udv + vdu. Lấy tích phân cả hai vế trên đoạn [a, b], ta thu được:
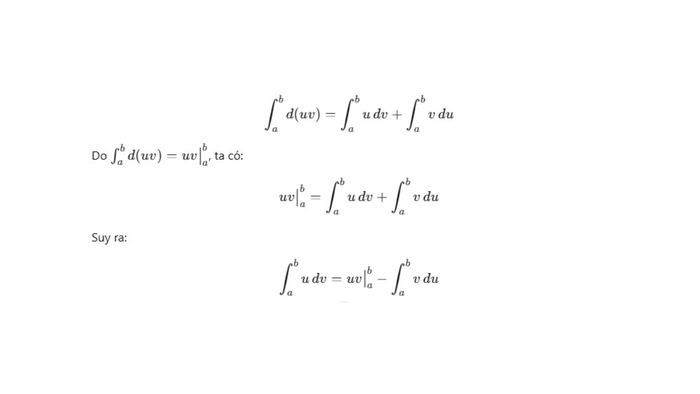
Học toán sẽ hiệu quả hơn khi bạn sử dụng iPad để ghi chép các công thức và bài tập tích phân từng phần. iPad không chỉ giúp sắp xếp bài vở khoa học mà còn hỗ trợ truy cập nhanh vào các ứng dụng giải toán trực tuyến. Hãy khám phá thêm về các dòng iPad phù hợp qua đường link bên dưới!
Một số dấu hiệu nhận biết nhanh
Trên thực tế, dấu hiệu nhận biết vấn đề này khá đơn giản. Người học chỉ cần tập trung vào đề bài là có thể dễ dàng nhận ra. Cụ thể, khi bài toán tích phân xuất hiện dạng tích của hai hàm số khác nhau, đó chính là dấu hiệu cho thấy cần áp dụng phương pháp tích phân từng phần. Hai hàm số trong dấu tích phân thường là sự kết hợp giữa các loại hàm như: logarit, đa thức, lượng giác và hàm mũ.
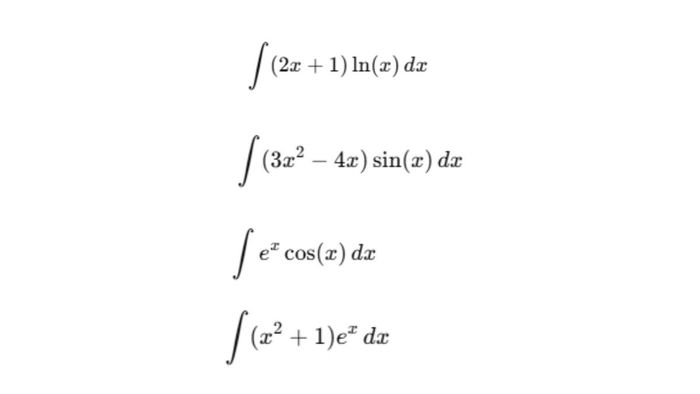
Các dạng bài tập tích phân từng phần
Các dạng bài tập phổ biến bao gồm tích phân của hàm đại số nhân với hàm mũ, hàm lượng giác hoặc hàm logarit. Mỗi dạng bài đều yêu cầu người giải nắm vững phương pháp và luyện tập thường xuyên để ghi nhớ lâu dài.
Tích phân của hàm đa thức và hàm logarit
Trong toán học, việc tính tích phân của hàm đa thức kết hợp với hàm logarit thường là thách thức đối với học sinh. Tuy nhiên, tham khảo ví dụ dưới đây sẽ giúp việc giải quyết bài toán trở nên dễ dàng hơn. Phương pháp này giúp chia nhỏ các bài toán phức tạp thành những phần đơn giản, phù hợp cho việc ôn tập và làm bài thi hiệu quả.
Cách thực hiện:

Ví dụ cụ thể:

Tích phân từng phần của hàm đa thức và hàm lượng giác
Tích phân của hàm đa thức và hàm lượng giác là dạng bài thường xuất hiện trong các đề thi. Áp dụng phương pháp dưới đây sẽ giúp bạn tính toán nhanh chóng, dễ dàng và chính xác. Khi nắm vững cách chọn u và dv, bạn sẽ tự tin hơn khi giải quyết dạng bài toán này trong thực tế.
Cách thực hiện:

Ví dụ cụ thể:
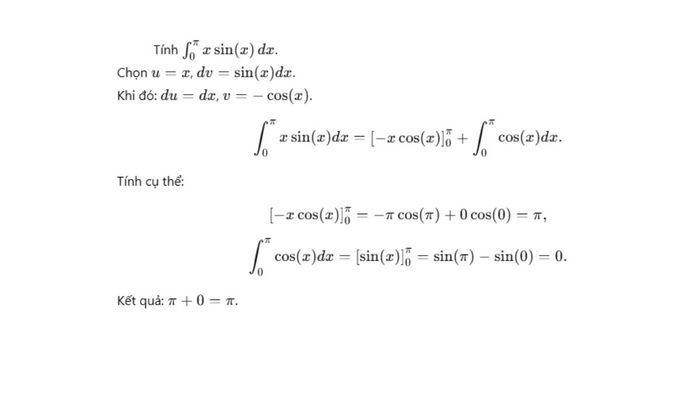
Hàm mũ và hàm lượng giác
Sự kết hợp giữa hai loại hàm này thường gây khó khăn trong việc giải tích phân. Tuy nhiên, với dạng bài này, bạn có thể chia nhỏ phép tính phức tạp thành các phần đơn giản hơn. Loại bài tập này không chỉ giúp rèn luyện tư duy mà còn củng cố kiến thức quan trọng, hỗ trợ hiệu quả cho việc học và thi cử. Vì vậy, hãy kiên trì và chăm chỉ luyện tập.
Cách thực hiện:
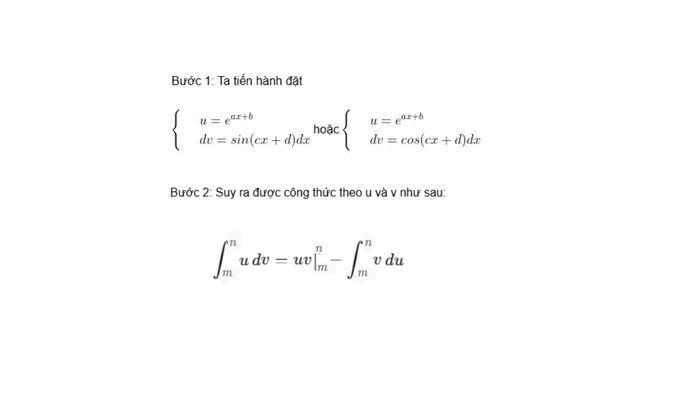
Ví dụ cụ thể:

Hàm mũ và hàm đa thức
Bài toán tích phân giữa hàm mũ và hàm đa thức thường được coi là khá phức tạp. Tuy nhiên, dạng toán này giúp bạn hiểu rõ hơn về mối quan hệ giữa các hàm số, đồng thời rèn luyện khả năng tư duy logic. Trong toán học, đây là kiến thức cơ bản và quan trọng mà bạn không nên bỏ qua.
Cách thực hiện:

Ví dụ cụ thể:
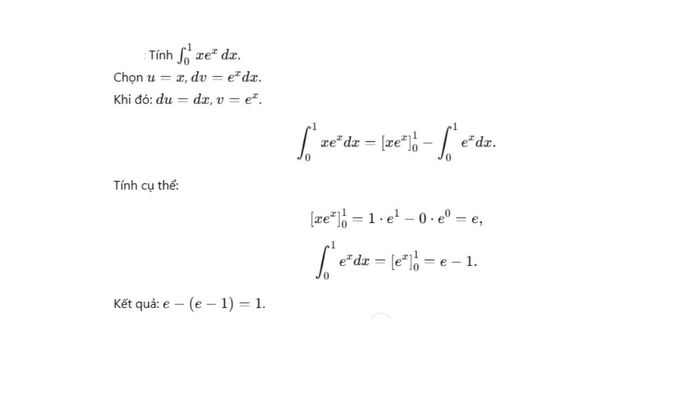
Mẹo chọn u và dv nhanh chóng
Để áp dụng công thức tích phân từng phần, cần biết cách đặt u và v. Việc này yêu cầu người giải tuân thủ quy tắc để đảm bảo kết quả chính xác. Hãy nhớ rằng u được chọn trước v. Thứ tự ưu tiên chọn u có thể ghi nhớ qua câu “Nhất Lô, nhì Đa, tam Lượng, tứ Mũ”. Ví dụ, nếu bài toán là tích của hàm logarit và đa thức, hàm logarit sẽ được chọn là u và đa thức là v.

Phương pháp và công thức tính tích phân từng phần đóng vai trò quan trọng trong việc giúp học sinh giải quyết các bài toán. Khi áp dụng phương pháp này, bạn không chỉ cải thiện khả năng phân tích mà còn tối ưu hóa thời gian làm bài. Hãy thường xuyên luyện tập các dạng bài tích phân từng phần để nắm vững kiến thức. Nếu muốn khám phá thêm các bài viết giáo dục, bạn có thể truy cập Mytour để cập nhật thông tin mới nhất!
Đọc thêm bài viết cùng chủ đề: Góc Học & Dạy 4.0
