Việc nắm bắt chính xác thông tin về góc giữa đường thẳng và mặt phẳng là rất quan trọng đối với học sinh ngày nay. Để thành thạo phần này, bạn cần hiểu rõ lý thuyết, làm quen với các phương pháp giải và áp dụng linh hoạt trong các bài tập trắc nghiệm. Bài viết dưới đây sẽ hướng dẫn bạn từng bước, giúp bạn tự tin giải quyết mọi bài toán liên quan đến chủ đề này.
Khái niệm góc giữa đường thẳng và mặt phẳng
Để giải quyết hiệu quả các bài toán hình học không gian, điều quan trọng nhất là bạn phải hiểu rõ khái niệm về góc giữa đường thẳng và mặt phẳng. Góc này diễn tả mối quan hệ giữa một đường thẳng và mặt phẳng, giúp chúng ta hình dung và giải thích cách thức tương tác của chúng trong không gian ba chiều. Việc hiểu và vận dụng chính xác khái niệm này sẽ giúp bạn giải quyết các bài toán hiệu quả hơn.
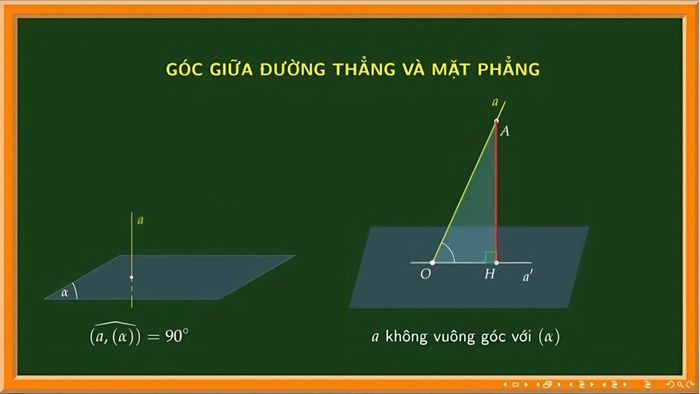
Góc giữa một đường thẳng và mặt phẳng là góc nhọn được tạo ra giữa đường thẳng và đường thẳng giao với nó trong mặt phẳng đó. Để làm rõ hơn định nghĩa này, hãy cùng xem xét hai trường hợp dưới đây:
Trường hợp 1:
- Nếu mặt phẳng (P) vuông góc với d - đường thẳng, thì góc giữa d và (P) là 900
- Trong trường hợp này, d và (P) không có hình chiếu vuông góc vì d đã hoàn toàn vuông góc với mặt phẳng.
Trường hợp 2:
- Trong trường hợp đường thẳng d không vuông góc với mặt phẳng (P), góc giữa d và (P) chính là góc giữa d và ảnh của nó trên mặt phẳng (P), ký hiệu là d'.
- Hình chiếu vuông góc của d trên mặt phẳng (P), hay nói cách khác là d', sẽ nằm hoàn toàn trong mặt phẳng (P) và tạo thành một góc có độ lớn nhỏ nhất với d.
Ký hiệu chi tiết cho góc giữa đường thẳng và mặt phẳng:
- Nếu d⊥(P) : ∠(d,(P)) = 900
- Nếu d không vuông góc với (P) : ∠(d,(P)) = ∠(d,d′), tức là góc giữa d và hình chiếu vuông góc d' của d trên mặt phẳng (P).
Hướng dẫn xác định góc giữa đường thẳng và mặt phẳng
Để đo được góc giữa mặt phẳng và đường thẳng, chúng ta cần có một nền tảng vững chắc về lý thuyết. Đây giống như một chiếc la bàn dẫn đường trong không gian hình học. Để giải quyết vấn đề này, bạn cần hiểu rõ các bước thực hiện và áp dụng đúng phương pháp cho từng tình huống cụ thể. Nhờ vậy, bạn sẽ nắm vững phương pháp giải quyết các bài tập trắc nghiệm hay bài toán nâng cao.
Phương pháp vecto tính góc giữa đường thẳng và mặt phẳng
Để tính góc giữa mặt phẳng và đường thẳng một cách chính xác, bạn cần hiểu rõ về công cụ hình học vecto. Phương pháp này dựa trên mối quan hệ giữa vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng. Trước tiên, bạn cần nắm bắt cách xác định góc giữa hai vecto này sao cho chính xác và trực quan nhất.
Để tính góc, bạn cần xác định vectơ pháp tuyến của mặt phẳng, ký hiệu là n, và vectơ chỉ phương, ký hiệu là u, của đường thẳng. Hai vecto này đóng vai trò quan trọng trong việc xác định góc giữa đường thẳng và mặt phẳng. Công thức tính góc được xây dựng dựa trên tích vô hướng của hai vecto, kết hợp với độ lớn (norm) của mỗi vecto để có kết quả chính xác.
Ví dụ, nếu d là đường thẳng với vectơ u = (a, b, c) và P là mặt phẳng với vectơ pháp tuyến (A, B, C), thì góc giữa đường thẳng và mặt phẳng sẽ được tính theo công thức đơn giản mà bạn có thể áp dụng dưới đây:
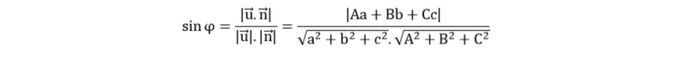
Khi làm các bài toán hình học không gian, việc xử lý chính xác các phép toán cùng lý thuyết là rất quan trọng, và điều này đòi hỏi một công cụ hỗ trợ tốt. Để học tập hiệu quả, một chiếc laptop cấu hình tốt sẽ giúp bạn xử lý nhanh chóng các bài toán phức tạp. Nếu bạn đang tìm kiếm thiết bị phù hợp, hãy tham khảo các dòng laptop giá sốc tại Mytour để có lựa chọn tốt cho việc học và làm bài, kèm theo nhiều ưu đãi cho giáo dục.
Cách xác định góc giữa đường thẳng và mặt phẳng bằng phương pháp hình học
Cách tính góc giữa đường thẳng và mặt phẳng thường dựa trên mối liên hệ giữa điểm chiếu của đường thẳng lên điểm cùng với chính đường thẳng đó. Cụ thể, góc của 2 điểm này được hiểu là góc nhọn tạo bởi điểm, hình chiếu của nó trên mặt phẳng.
Để giải bài toán tìm góc giữa đường thẳng a và mặt phẳng (α) bằng hình học, bạn làm tuần tự các bước dưới đây. Trước tiên, cần biết được vectơ pháp tuyến của mặt phẳng (α) vectơ của a (chỉ phương). Sau đó, áp dụng công thức tính góc dựa trên mối quan hệ giữa hai vectơ này để tìm ra giá trị chính xác của góc cần tìm.
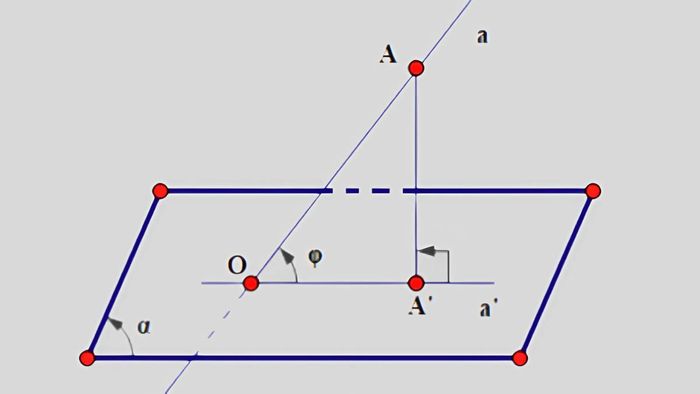
Bước 1: Tìm điểm chung O
Để tìm góc giữa a và (α), bước đầu tiên là xác định điểm O, nơi đường thẳng a cắt mặt phẳng (α). Đây là điểm mà đường thẳng, bề phẳng cắt nhau và nó đóng vai trò làm gốc để xác định mối quan hệ giữa 2 vật thể này.
Bước 2: Thực hiện phép chiếu vuông góc điểm lên mặt phẳng.
Chọn điểm A trên đường thẳng a, thực hiện chiếu vuông góc từ A lên mặt phẳng (α). Điểm chiếu này được ký hiệu là A′, và để vẽ hình chiếu, bạn cần vẽ một đường thẳng vuông góc từ A đến mặt phẳng (α), sao cho điểm A′ nằm trong mặt phẳng đó.
Bước 3: Tính góc nhanh chóng
Từ điểm giao O giữa đường thẳng a và mặt phẳng (α), dựng một đoạn thẳng vuông góc AA' từ điểm A trên đường thẳng a đến mặt phẳng (α). Góc ∠AOA' chính là góc giữa a và (α). Để tính giá trị của góc này, bạn có thể dùng dụng cụ đo góc hoặc áp dụng các định lý hình học đã học.
Bài tập trắc nghiệm minh họa góc giữa đường thẳng và mặt phẳng
Dưới đây là một số bài tập trắc nghiệm giúp bạn hiểu rõ hơn về cách xác định góc trong các tình huống khác nhau.

Câu 1: Cho ΔABC vuông tại A, với cạnh AB = a và cạnh AC = a3. Từ điểm A, kẻ một đường vuông góc với mặt phẳng (ABC). Trên đường thẳng này, lấy điểm S sao cho đoạn thẳng SA có độ dài bằng 2a. Hãy xác định góc tạo bởi cạnh bên SA và mặt phẳng đáy (ABC)?
A. 3000
B. 4500
C. 6000
D. 9000
Lời giải:
Vì SA vuông góc với mặt phẳng (ABC), ta có
SA⊥(ABC) ⟹ ∠(SA,(ABC)) = 900⟹ ∠(SA,(ABC)) = 9000
Do đó, góc giữa SA và (ABC) là 900. Vì vậy, D là đáp án chính xác.
Câu 2: Cho hình chóp P.MNOP với đáy MNO đều có cạnh bằng b. G là giao điểm của đường vuông góc hạ từ P xuống mặt phẳng (MNO). Khi đó, G không chỉ là hình chiếu của P mà còn là trung điểm của đoạn thẳng NO. Hơn nữa, PNO là tam giác đều. Tính góc giữa mặt phẳng (MNO) và PM?
A. 3000
B. 4500
C. 6000
D. 9000
Lời giải:
Vì PG vuông góc với mặt phẳng (MNO), ta có:
PG⊥(MNO)
Do đó, MG là hình chiếu của PM lên mặt phẳng (MNO), nên ta có:
∠(PM,(MNO)) = ∠(PM,MG) = ∠(PMG)
Xét tam giác PMG
- PG vuông góc với (MNO) nên PG vuông góc với MGP
- Vì tam giác PNO đều, ta có PG = MGP
- Tam giác PMG vuông cân tại G, nên ∠(PMG) = 4500
Do đó, B là đáp án chính xác.
Khả năng ứng dụng kiến thức về góc giữa đường thẳng và mặt phẳng là yếu tố quan trọng giúp học sinh nhanh chóng giải quyết bài toán mà không phải lo lắng quá nhiều. Việc nắm vững phương pháp và áp dụng chính xác vào các bài tập trắc nghiệm sẽ giúp bạn đạt kết quả tốt trong các kỳ thi. Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn và tự tin hơn khi giải các bài tập liên quan đến chủ đề này.
