Việc hiểu rõ cách tính khoảng tứ phân vị có ý nghĩa quan trọng trong thống kê, giúp đánh giá mức độ phân tán của dữ liệu. Đối với dữ liệu được phân nhóm, việc xác định khoảng tứ phân vị cho phép chúng ta nắm bắt được phạm vi chứa phần lớn các giá trị quan sát. Nắm vững phương pháp này không chỉ cải thiện hiệu quả phân tích mà còn đảm bảo độ chính xác cao trong các nghiên cứu và báo cáo thống kê.
Giới thiệu về khoảng biến thiên và khoảng tứ phân vị trong chương trình Toán lớp 12
Trong khi khoảng biến thiên thể hiện sự khác biệt giữa giá trị cao nhất và thấp nhất của tập dữ liệu, khoảng tứ phân vị lại tập trung vào phạm vi chứa phần lớn các giá trị. Vậy khoảng tứ phân vị là gì và cách tính toán nó ra sao? Hãy cùng Mytour khám phá chi tiết trong bài viết này.
Khoảng biến thiên
Khoảng biến thiên là một chỉ số thống kê quan trọng, thể hiện sự phân tán của dữ liệu thông qua việc đo lường khoảng cách giữa giá trị cao nhất và thấp nhất trong tập hợp.
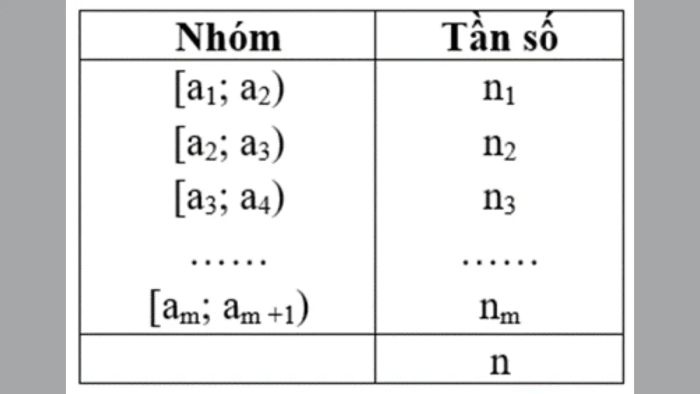
Trong trường hợp dữ liệu được ghép nhóm, khoảng biến thiên được tính bằng hiệu số giữa điểm cuối của nhóm cuối cùng và điểm đầu của nhóm đầu tiên. Công thức R=am+1 -a1 giúp xác định mức độ biến động của tập dữ liệu.
Khoảng tứ phân vị
Khoảng tứ phân vị là một chỉ số thống kê dùng để đo lường sự phân tán của dữ liệu, được xác định bằng khoảng cách giữa tứ phân vị thứ ba (Q3) và tứ phân vị thứ nhất (Q1). Đối với dữ liệu ghép nhóm, Q1 và Q3 được tính toán thông qua phương pháp nội suy dựa trên tần số tích lũy.

Khoảng tứ phân vị được xác định bằng công thức Q=Q3-Q1, giúp đánh giá sự biến động của phần lớn dữ liệu mà không bị ảnh hưởng bởi các giá trị ngoại lệ, từ đó nâng cao độ chính xác trong phân tích thống kê.
Ví dụ minh họa về khoảng tứ phân vị (Hướng dẫn giải chi tiết)
Để nắm rõ hơn về ý nghĩa và cách áp dụng khoảng tứ phân vị, chúng ta sẽ cùng phân tích một ví dụ cụ thể kèm theo hướng dẫn giải chi tiết. Việc sử dụng khoảng tứ phân vị trong thực tế giúp xác định mức độ phân tán của phần lớn dữ liệu, từ đó đưa ra những nhận định chính xác về đặc điểm và xu hướng của tập dữ liệu.
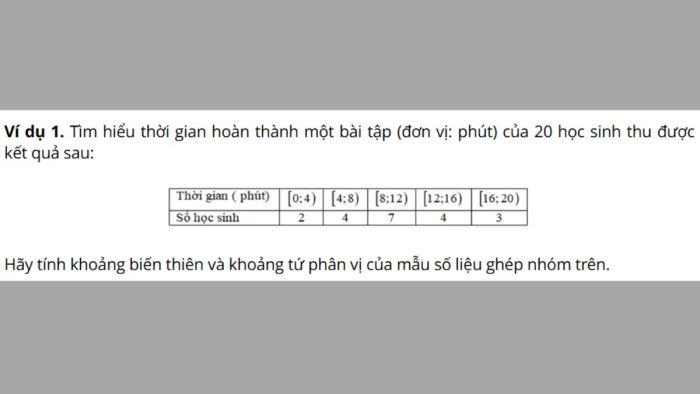



Thông qua các bước giải chi tiết, bạn sẽ hiểu rõ cách tìm khoảng tứ phân vị cũng như phương pháp tính toán để xác định phạm vi biến động của dữ liệu mà không bị tác động bởi các giá trị ngoại lệ.
Bài tập thực hành về khoảng biến thiên và khoảng tứ phân vị trong chương trình Toán 12
Sau khi nắm chắc lý thuyết, việc áp dụng vào các bài tập thực hành sẽ giúp bạn hiểu sâu hơn về cách xác định khoảng biến thiên và khoảng tứ phân vị trong phân tích thống kê.
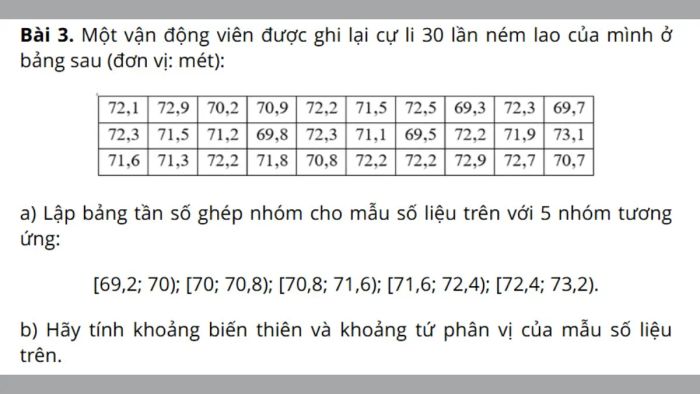
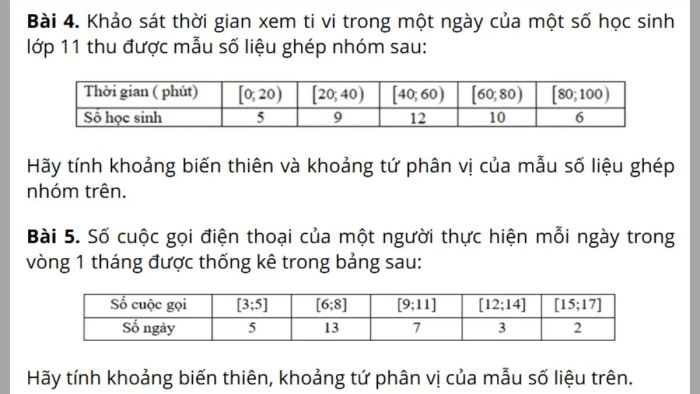
Áp dụng công thức vào các bài toán cụ thể không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng tính toán và phân tích dữ liệu. Đặc biệt, khi xác định khoảng tứ phân vị, bạn sẽ nhận thấy rõ hơn cách các tứ phân vị thể hiện sự phân bố của dữ liệu và mức độ biến động của tập hợp số liệu.
Việc xác định khoảng tứ phân vị cho dữ liệu ghép nhóm giúp làm rõ sự phân bố của dữ liệu, mang lại góc nhìn trực quan hơn về mức độ phân tán. Khi đã hiểu rõ cách tính khoảng tứ phân vị, bạn có thể áp dụng linh hoạt trong nhiều tình huống thực tế, từ nghiên cứu học thuật đến phân tích dữ liệu kinh doanh. Hy vọng bài viết này đã cung cấp những thông tin hữu ích, giúp bạn hiểu và áp dụng phương pháp tính toán này một cách chính xác.
