Phương trình elip là một chủ đề toán học quan trọng trong chương trình phổ thông, thường được đánh giá là khó. Những đặc điểm, công thức, và lưu ý khi giải quyết dạng bài này là gì? Nếu bạn muốn củng cố kiến thức hoặc tìm hiểu cách xây dựng phương trình chính tắc tổng quát của elip, hãy khám phá những thông tin dưới đây.
Khái niệm cơ bản về phương trình đường elip
Để nắm vững định nghĩa của phương trình đường elip, hãy tham khảo phần lý thuyết sau:
Xét hai điểm cố định F1 và F2 trên mặt phẳng cùng với khoảng cách 2a không đổi, lớn hơn độ dài F1F2. Elip là tập hợp tất cả các điểm M trong mặt phẳng thỏa mãn điều kiện F1M + F2M = 2a.
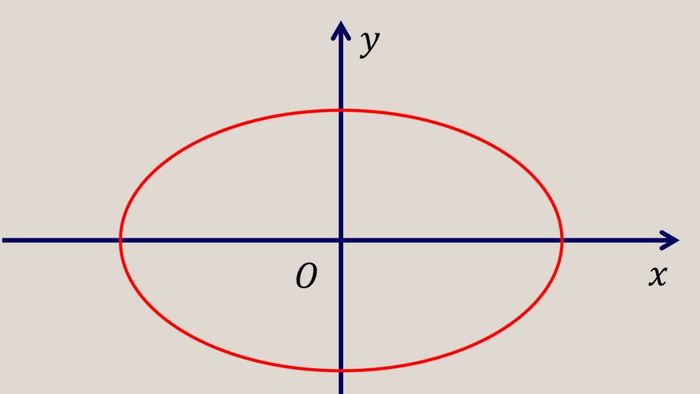
Trên thực tế, đường elip có hình dạng tương tự hình tròn nên sở hữu nhiều tính chất liên quan. Trong hình học, hai điểm F1 và F2 được gọi là tiêu điểm, còn khoảng cách giữa chúng (F1F2) được gọi là tiêu cự của elip.
Để khám phá thêm các dạng bài tập khác, bạn cần một chiếc laptop để hỗ trợ việc học tập hiệu quả. Dưới đây là một số gợi ý về laptop phù hợp cho nhu cầu học tập:
Phương trình chính tắc của elip được định nghĩa như thế nào?
Phương trình chính tắc của elip là một phần quan trọng trong các bài toán hình học phẳng. Học sinh cần nắm vững kiến thức này để giải quyết tốt các bài toán hình học và ứng dụng vào thực tế.
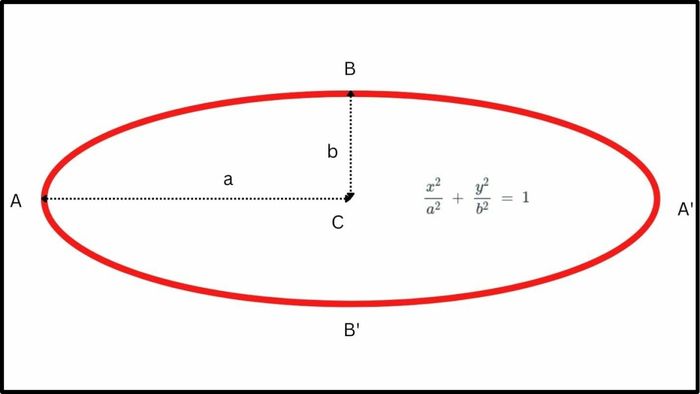
Xét elip với hai tiêu điểm F1 (-c;0) và F2 (c;0) trong hệ trục tọa độ Oxy. Điểm M thuộc elip khi và chỉ khi tổng khoảng cách từ M đến F1 và F2 bằng 2a. Từ đó, phương trình chính tắc của elip được xác định như sau:
M (x, y) ∈ (E) ⇔ x²/a² + y²/b² = 1. Trong đó: b² = a² - c²
Các yếu tố và đặc điểm hình dạng của elip
Sau khi nắm được phương trình tổng quát của elip, bạn cần hiểu rõ hơn về các thành phần cấu tạo nên hình dạng này. Elip có hình dạng tương tự hình tròn với các thành phần đối xứng qua hệ trục tọa độ. Cụ thể, các thành phần chính của elip bao gồm:
- Xét elip (E) và điểm M (x;y) thuộc (E). Khi đó, các điểm M1 (-x;y), M2 (x; -y) và M3 (-x, -y) cũng thuộc (E).
- Hai tiêu điểm của elip có tọa độ lần lượt là F1 (-c;0) và F2 (c;0).
- Bốn đỉnh của elip là A1 (-a;0), A2 (a;0), B1 (0;-b) và B2 (0;b). Các đỉnh này là giao điểm giữa elip và hai trục Ox, Oy trong hệ tọa độ.
- F1F2 = 2c, đây chính là tiêu cự của elip.
- Khoảng cách A1A2 = 2a được gọi là độ dài trục lớn của elip.
- Khoảng cách B1B2 = 2b là độ dài trục nhỏ của elip.
Mối quan hệ giữa hình tròn và elip
Hình tròn và elip có mối liên hệ chặt chẽ về mặt hình học. Do đó, các nghiên cứu về hình tròn sẽ giúp bổ sung tính chất cho phương trình elip và ngược lại.
- Tính đối xứng và phương pháp tính diện tích
Cả hình tròn và elip đều có tính đối xứng qua tâm O và các trục chính Ox, Oy. Việc tính diện tích của hai hình này đều dựa trên bán kính (đối với hình tròn) hoặc bán trục (đối với elip) cùng giá trị .
phuong-trinh-elip-4
- Elip có thể tiến gần đến hình dạng của hình tròn
Từ biểu thức b² = a² - c², ta có thể thấy rằng khi tiêu cự của elip càng nhỏ, giá trị b càng tiến gần đến a. Điều này cho thấy trục nhỏ của elip có độ dài gần bằng trục lớn. Như vậy, elip càng có tiêu cự nhỏ thì hình dạng của nó càng giống với hình tròn.
- Hình tròn có thể biến đổi thành elip
Ngược lại với mối quan hệ trên, hình tròn có thể biến đổi thành elip nếu đáp ứng một số điều kiện nhất định. Cách chứng minh như sau:
Xét hình tròn (O) có phương trình x² + y² = a². Mọi điểm M (x;y) đều thuộc đường tròn O. Xét điểm M’(x’;y’) thỏa mãn hai điều kiện: x’ = x và y’ = (b/a) y. Khi đó, tập hợp các điểm M’ sẽ thỏa mãn phương trình chính tắc của elip: x’²/a² + y’²/b² = 1.
Từ các chứng minh trên, ta có thể kết luận rằng: Hình tròn có thể biến đổi thành elip.
Một số bài tập thực hành
Để nắm vững cách áp dụng phương trình elip trong toán học, bạn có thể tham khảo một số bài tập kèm lời giải chi tiết dưới đây:
Bài 1: Cho elip (E) có phương trình x²/25 + y²/9 = 1. Hãy xác định độ dài trục lớn, trục nhỏ, tiêu điểm và tiêu cự của elip này.
Lời giải:
Từ phương trình x²/25 + y²/9 = 1 của elip (E), ta suy ra:
a² = 25 ⇒ a = 5
b² = 9 ⇒ b = 3
c = √(a² - b²) = √(25 - 9) = √16 = 4
Từ các giá trị trên, ta tính được độ dài trục lớn, trục nhỏ, tiêu điểm, tiêu cự và tâm sai của elip (E) như sau:
Tiêu điểm của elip (E): F1 (-4;0) và F2 (4;0)
Tiêu cự của elip (E): F1F2 = 4 + 4 = 8
Độ dài trục lớn: A1A2 = 2a = 5 × 2 = 10
Độ dài trục nhỏ: B1B2 = 2b = 2 × 3 = 6

Bài 2: Cho elip (E) có độ dài trục lớn là 12 và trục nhỏ là 8. Hãy viết phương trình chính tắc của elip (E) dựa trên thông tin đã cho.
Lời giải:
Gọi các đỉnh của elip là A1 (-a;0), A2 (a;0), B1 (0;-b) và B2 (0;b).
Độ dài trục lớn: A1A2 = 2a = 12 ⇒ a = 6
Độ dài trục nhỏ: B1B2 = 2b = 8 ⇒ b = 4
Phương trình elip của (E) được biểu diễn như sau: x²/a² + y²/b² = 1 ⇒ x²/25 + y²/9 = 1
Trên đây là những kiến thức cơ bản về phương trình elip. Bên cạnh dạng bài lập phương trình chính tắc tổng quát, còn nhiều dạng bài tập khó khác mà bạn cần ôn tập kỹ lưỡng. Để tìm hiểu thêm về các dạng toán này, hãy khám phá các bài viết về toán học và chủ đề giáo dục trên Mytour.
Khám phá thêm các bài viết cùng chuyên mục: Góc Học & Dạy 4.0
