Bạn đã hiểu rõ cách vẽ, các đặc điểm và tính chất của hình lục giác đều chưa? Loại đa giác này không chỉ sở hữu nhiều tính chất thú vị mà còn xuất hiện khá nhiều trong cuộc sống xung quanh. Mytour đã tổng hợp đầy đủ kiến thức từ lý thuyết cơ bản đến cách ứng dụng thực tế trong bài viết này, hãy cùng tìm hiểu nhé!
Hình lục giác đều là gì?
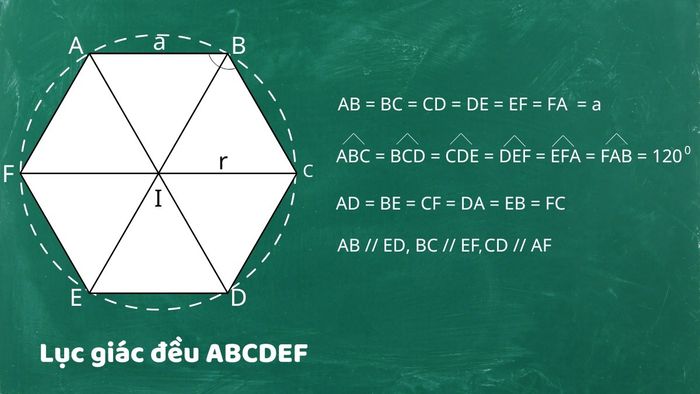
Hình lục giác đều là một loại đa giác đặc biệt với 6 cạnh bằng nhau và 6 góc trong đều bằng 120 độ. Đường chéo của hình này cũng có độ dài bằng nhau và giao nhau tại tâm đối xứng. Hình lục giác đều rất phổ biến trong tự nhiên, ví dụ như trong tổ ong và các tinh thể. Trong toán học, hình này cũng xuất hiện trong các bài toán về diện tích, chu vi và các ứng dụng trong kiến trúc, nghệ thuật,...

Những đặc điểm nổi bật của hình lục giác đều
Hình lục giác đều mang trong mình những tính chất độc đáo khiến nó trở thành một trong những đa giác đặc biệt nhất, bao gồm các đặc điểm sau:
- Độ dài của tất cả 6 cạnh đều bằng nhau
- Các góc trong đều có giá trị 120 độ
- Các cạnh đối diện có tính chất song song với nhau
- Đo dài các đường chéo nối các đỉnh đối diện, chúng đều bằng nhau
- Tâm đối xứng nằm tại điểm giao của các đường chéo chính
- Hình lục giác đều có sáu trục đối xứng, mỗi trục đều đi qua tâm và các điểm giữa các cạnh
Một chiếc iPad với màn hình sắc nét cùng hiệu suất vượt trội sẽ là công cụ học tập tuyệt vời, đặc biệt khi giải quyết các bài toán hình học. Nếu bạn đang tìm kiếm một thiết bị mới, đừng quên tham khảo các mẫu iPad chính hãng tại Mytour qua đường link dưới đây. Khám phá ngay nhé!
Các công thức tính toán liên quan đến hình lục giác đều
Hình lục giác đều không chỉ nổi bật nhờ tính đối xứng mà còn liên quan đến nhiều công thức toán học quan trọng. Để hiểu rõ cách tính chu vi và diện tích hình này, hãy tham khảo các công thức mà Mytour đã tổng hợp dưới đây!
Công thức tính chu vi hình lục giác đều
Vì các cạnh của hình lục giác đều có độ dài bằng nhau, việc tính chu vi trở nên đơn giản hơn rất nhiều. Bạn chỉ cần biết độ dài của một cạnh và nhân với 6 để có được chu vi của đa giác này. Công thức tính chu vi là:
P = 6a
Công thức tính chu vi của hình lục giác đều là:
- a: Độ dài của mỗi cạnh của hình lục giác đều
- P: Chu vi của hình lục giác đều
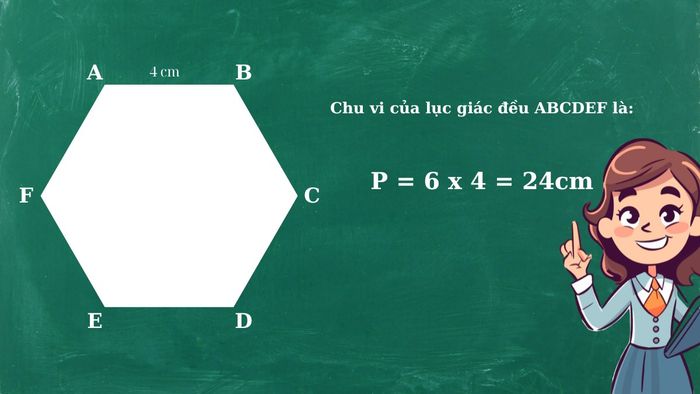
Ví dụ, với một hình lục giác đều có các cạnh dài 4cm, chu vi sẽ được tính như sau:
P = 6 x 4 = 24cm
Công thức tính diện tích
Tính diện tích của hình lục giác đều không chỉ là một bài toán quen thuộc trong hình học mà còn có ứng dụng rộng rãi trong đời sống. Với đặc tính đối xứng rõ ràng, hình lục giác đều có một công thức tính diện tích rất đơn giản. Công thức tính diện tích như sau:
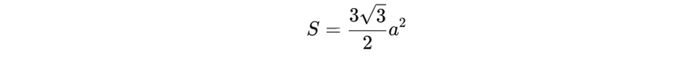
Trong đó:
- S: Diện tích của hình lục giác đều
- a: Độ dài của mỗi cạnh hình lục giác đều
Ví dụ: Cho một hình lục giác đều có cạnh dài 4cm, hãy tính diện tích của hình này.
Lời giải chi tiết:
Diện tích của hình lục giác đều này được tính như sau:
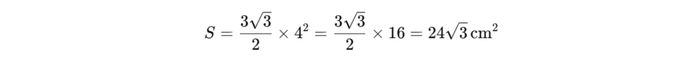
Công thức tính độ dài đường chéo của hình lục giác đều
Hình lục giác đều có 6 đỉnh và tạo ra 9 đường chéo. Trong đó, các đường chéo chính là những đường nối hai đỉnh đối diện với nhau. Công thức tính độ dài đường chéo chính là:
d=2a
Trong đó:
d: Độ dài của đường chéo chính trong hình lục giác đều
a: Độ dài của một cạnh trong hình lục giác đều
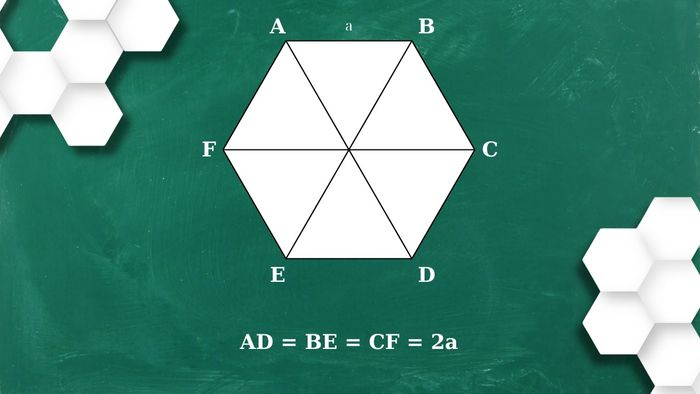
Ví dụ: Tính độ dài của đường chéo AD trong hình lục giác đều ABCDEF với chiều dài cạnh là 4cm.
Lời giải: AD = 2 x 4 = 8cm
Cách vẽ hình lục giác đều nhanh chóng và chính xác
Vẽ hình lục giác đều rất đơn giản, bạn chỉ cần chuẩn bị vài dụng cụ cơ bản như compa, thước thẳng và bút. Các bước vẽ hình cụ thể như sau:
- Bước 1: Chọn một điểm làm tâm, sau đó dùng compa vẽ một đường tròn có bán kính r.
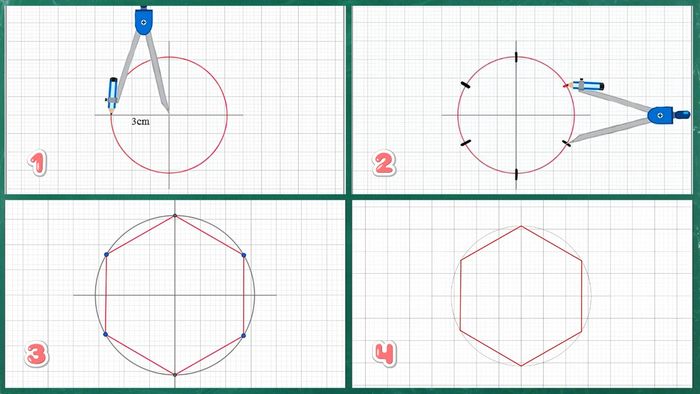
- Bước 2: Giữ nguyên độ mở của compa, chia đường tròn thành 6 phần đều nhau.
- Bước 3: Kết nối các điểm vừa chia trên đường tròn để tạo thành hình lục giác đều với các cạnh dài bằng r. Đường tròn này cũng chính là đường tròn ngoại tiếp của hình.
- Bước 4: Nếu chỉ cần vẽ hình lục giác đều, bạn chỉ cần xóa các đường phụ và hoàn thành.
Các câu hỏi thường gặp liên quan đến hình lục giác đều
Trước đó, Mytour đã chia sẻ với bạn những kiến thức về cách vẽ, tính chất và diện tích của hình lục giác đều. Đây là những thông tin cơ bản rất quan trọng khi tìm hiểu về loại đa giác đặc biệt này. Nếu bạn vẫn còn bất kỳ thắc mắc nào, hãy tiếp tục theo dõi bài viết này để Mytour giải đáp thêm cho bạn nhé!
Hình lục giác đều có bao nhiêu đường chéo?
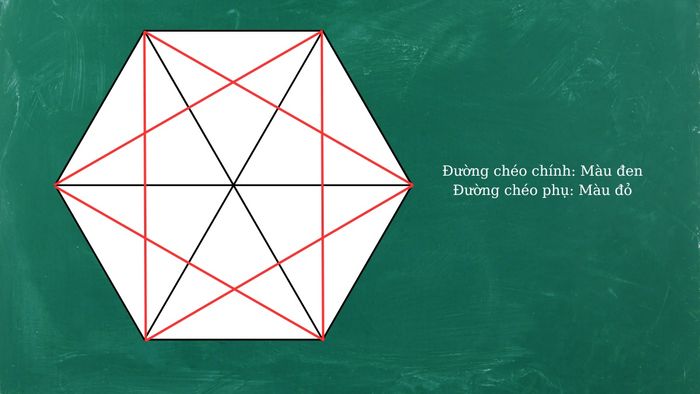
Hình lục giác đều có tổng cộng 9 đường chéo, bao gồm:
- Đường chéo chính: 3 đường, được vẽ nối giữa hai đỉnh đối diện. Các đường chéo này chia hình lục giác đều thành hai phần bằng nhau, với độ dài bằng đường kính của đường tròn ngoại tiếp.
- Đường chéo phụ: 6 đường, nối hai đỉnh không kề nhau (không tính các đỉnh đối diện).
Góc trong của hình lục giác đều là bao nhiêu?
Mỗi góc trong của hình lục giác đều luôn có giá trị là 120 độ. Đây là một đặc điểm quan trọng giúp bạn nhận diện và phân biệt hình lục giác đều với các loại đa giác khác. Một điểm thú vị là, khi các đường chéo chính chia hình lục giác đều thành các tam giác, tất cả chúng đều là những tam giác đều và hoàn toàn giống nhau.

Hình lục giác đều có bao nhiêu trục và tâm đối xứng?
Hình lục giác đều có tính đối xứng hoàn hảo với 6 trục đối xứng và 1 tâm đối xứng. Cụ thể là:
- Tâm đối xứng: Là điểm giao nhau của các đường chéo chính. Khi bạn xoay hình lục giác đều một góc 60 độ quanh tâm, hình sẽ trùng khít với chính nó.
- Trục đối xứng: Là những đường thẳng đi qua tâm và trung điểm của mỗi cạnh bất kỳ.

Mytour đã cung cấp cho bạn những kiến thức hữu ích về cách vẽ, tính chất, và diện tích của hình lục giác đều trong bài viết trước. Hy vọng rằng bạn sẽ áp dụng được những kiến thức này để giải quyết các bài toán hình học một cách nhanh chóng và chính xác. Để khám phá thêm những thông tin bổ ích khác, đừng quên theo dõi những bài viết cùng chủ đề giáo dục trên Mytour nhé!
Khám phá thêm các bài viết trong chuyên mục: Góc Học & Dạy 4.0
